4.1. Solución aproximada de ecuaciones#

Introducción: planteamiento del problema
Método Lineal: el caso del cálculo de raíz de un número
Método de la bisección
Método de Newton-Raphson: el caso de la raíz de un número

4.1.1. Introducción: planteamiento del problema#

4.1.1.1. Lo que buscamos: Solución aproximada de una ecuación con error dado#

Cuando hablamos de la solución de una ecuación, por ejemplo la ecuación $x^3-7x^2+23 = 0,$ queremos decir que quremos obtener el valor o valores de $x$ que verifican dicha ecuación. Si $f(x) = x^3-7x^2+23$ también decimos que estamos buscando los ceros de la función $f(x),$ es decir, los valores de $x$ que verifican la ecuación $f(x) = 0.$ En términos geométricos, estamos buscando los puntos de intersección de la gráfica de $f(x)$ con el eje de la $x$’s.

Si $x^{*}$ es una solución de la ecuación planteada, $f(x) = 0,$ decimos que $x_{ap}$ es un valor aproximado de $x^{*}$ con error no mayor que $\varepsilon$ si

\[ |x^{*}-x_{ap}|<\varepsilon. \]

Geométricamente, esto significa que $x^{*}$ y $x_{ap}$ se encuentran dentro de un intervalo de longitud $\varepsilon$. La anterior desigualdad también implica que $x_{ap}$ e encuantra en un intervalo de longitud $2\varepsilon$ centrado en $x^{*}.$ En términos matemáticosse puede escribir de forma equivalente:

\[ x_{ap}\in(x^{*}+\varepsilon ,x^{*} +\varepsilon) \]

4.1.1.2. Herramienta: El teorema de Bolzano#

El teorema de Bolzano asegura que si $f$ es una función continua en el intervalo $[a,b]$ y que toma valores de diferente signo en los extremos del intervalo, es decir,

\[ f(a)\cdot f(b)<0, \]

entonces existe una solución $x^{*}$ de la ecuación $f(x)=0$ en $[a,b]$.

El teorma de Bolzano no nos dice el valor de la solución, solo asegura su existencia. Pero del hecho que esta solución está en $[a,b]$ sabemos que si escogemos un valor aproximado $x_{ap}\in[a,b]$ entonces (¿por qué?)

\[ |x^{*}-x_{ap}|<b-a. \]

Esto significa que el error de aproximar $x^{*}$ por $x_{ap}$ es menor que $b-a$.

En particular, si escogemos el punto medio de $[a,b]$

\[ x_{ap}=\frac{a+b}{2}, \]

se puede garantizar que el error es aún menor (¿por qué?)

\[ |x^{*}-x_{ap}|<\frac{b-a}{2}. \]

4.1.2. Método de búsqueda lineal: el caso del cálculo de la raíz de un número#

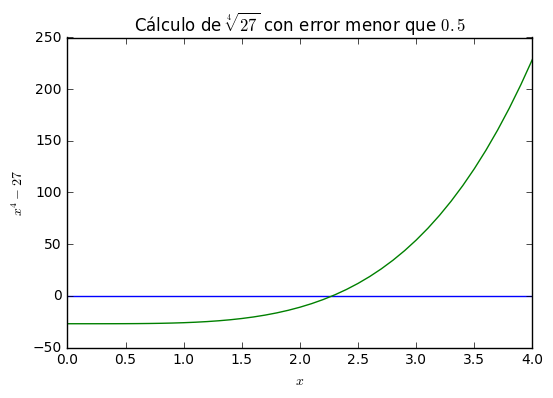
Nuestra estrategia para encontrar una solución aproximada de la ecuación $f(x)=0$ en $[a,b],$ dónde se verifica el teorema de Bolzano, va a er la siguiente: dividiremos el intervalo original $[a,b]$ en subintervalos pequeños de longitud menor que $\varepsilon$ e iremos comprobando en ellos si se cumple la condición de Bolzano (búsqueda lineal).

Esta sería una descripción detallada del correspondiente algoritmo para el cálculo de la raíz cuarta de un número:

Define la función partición(a,b,eps) que devuelve la lista

\[ [x_0 = a, x_1, \dots , x_n = b]\]

de puntos que dividen el intervalo $(a,b)$ en $n$ partes iguales de longitud menor que eps.

Define la función sol_lineal(f,a,b,eps) que devuelve un valor aproximado de la solución en (a,b) con error menor que $\varepsilon.$ Si no hay, devuelve False.

Define la función raiz4_lineal(a) que calcula la raíz cuarta del número positivo $a$ utilizando la función sol_lineal() aplicada a $f(x)=x^{4}-a$ en el intervalo $[0,1+a]$ con $\varepsilon=0.0001$ ¿ Cumple $f$ la condición de Bolzano en ese intervalo? ¿Por qué?

Ejercicios

Define la función pasos_lineal(a) que devuelve el número de pasos que se realizan al calcular raiz4_lineal(), es decir, el número de subintervalos que hay que comprobar hasta obtener el resultado deseado.

Utiliza las funciones bolzano() y sol_lineal() para encontrar todas las soluciones de la ecuación

\[ x^{3}-5x^{2}-2x+1=0 \]

Dibujar la función $f(x) = x^{3}-5x^{2}-2x+1=0$ para determinar el espacio de búsqueda.

Definir una función que implemente el siguiente esquema para la búsqueda del valor aproximado de la solución con un número determinado de cifras decimales (búsqueda con paso variable):

dividir el intervalo $(a,b)$ en $10(b-a)$ partes iguales y seleccionar aquella donde se cumple la condición de Bolzano
repetir el proceso en la parte seleccionada hasta obtener el numero de cifras exactas de la solución busquemos.

4.1.3. Método de la bisección#

El teorema de Bolzano ayuda en realidad a escoger un valor aproximado de la solución de $f(x)=0$ en $[a,b]$ con error tan pequeño como deseemos.

Si encontramos un intervalo $[p,q]\subset [a,b]$ tal que

\[f(p)\cdot f(q)<0\]

que sea suficientemente pequeño: $q-p < \varepsilon,$ entonces, si escogemos cualquier valor

\[ x_{app} \in (p,q)\]

tendremos

\[|x^*-x_{ap}| < q-p < \varepsilon.\]

Más aún, si se escoge

\[x_{ap} = \frac{p+q}{2}\]

resultará que

\[|x^*-x_{ap}| < \frac{\varepsilon}{2}.\]

Ejercicio

Define la función bolzano(f,a,b) donde $f$ es una función continua definida en el intervalo $[a,b]$. Debe devolver True o False según se cumpla la condición de Bolzano en $[a,b]$ o no.

Por ejemplo, si $f(x) = \sin(x),$ $a = -\pi/2$ y $b = \pi/2,$ la función devuelve True, dado que $f(-\pi/2)\cdot f(\pi/2)\leq 0.$

Observa que el parámetro f de la función bolzano(f,a,b) corespondería, en el ejemplo anterior, a

def f(x):
    import math
    return math.sin(x)

Es decir, hay que definir la función f antes de invocar la función bolzano(f,a,b).

Resumen

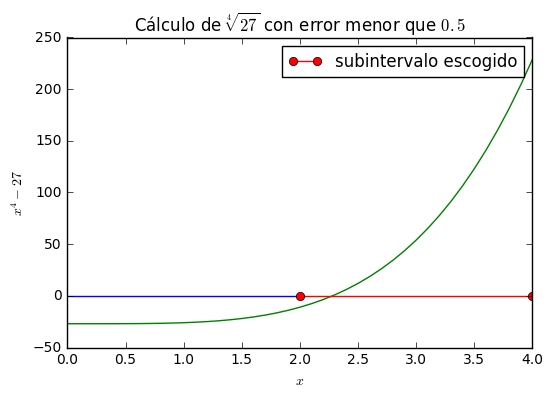
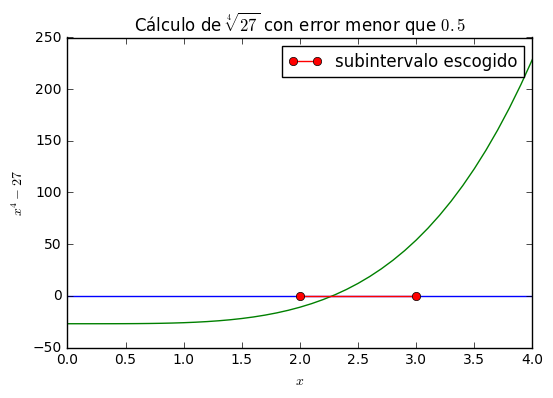
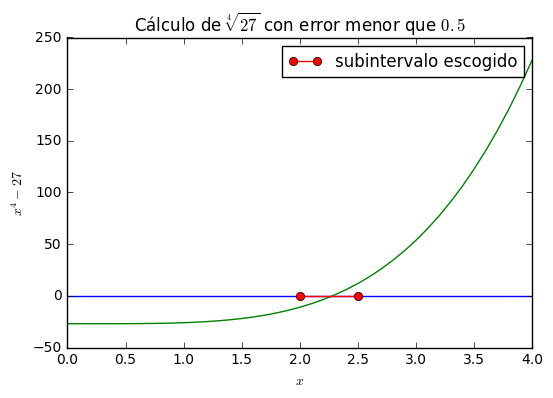
El teorema de Bolzano ayuda en realidad a escoger un valor aproximado de la solución de $f(x)=0$ en $[a,b]$ con error tan pequeño como deseemos. El método de bisección consiste en ir dividiendo progresivamente el intervalo a la mitad y conservando solo aquella parte dónde se encuentra la solución (es decir, aquella dónde se cumple la condición de Bolzano (véase las figuras de más abajo). Como en cada paso la longitud del intervalo se reduce a la mitad, ésta podrá llegar a ser más pequeña que cualquier número $\varepsilon<0$ dado. Entonces, el punto medio de ese intervalo cuya longitud sea menor que el error establecido, será una aproximación adecuada.

Ejercicios

Define las funciones cortar_inf(f,a,b) y cortar_sup(f,a,b) donde $f$ es una función continua que cumple la condición de Bolzano en el intervalo $[a,b]$. Se trata de dividir el intervalo $[a,b]$ en dos subintervalos iguales (es decir, a la mitad) y escoger, utilizando el teorema de Bolzano, aquel dónde se encuentra la solución. La función cortar_inf(f,a,b) devuelve el extremo inferior del intervalo seleccionado y la funcion cortar_sup(f,a,b) el superior. El programa debe comprobar si la función cumple la condición de Bolzano en $[a,b]$ y devolver una cadena vacía en caso de que no se cumpla.

Alternativa: Define la función cortar(f,a,b) donde $f$ es una función continua que cumple la condición de Bolzano en el intervalo $[a,b]$. La función cortar(f,a,b) divide el intervalo $[a,b]$ en dos subintervalos iguales (es decir, a la mitad) y escoge, utilizando el teorema de Bolzano, aquel donde se encuentra la solución. Finalmente, devuelve el intervalo seleccionado en forma de lista de Python. El programa debe comprobar si la función cumple la condición de Bolzano en $[a,b]$ y devolver una lista vacía en caso de que no se cumpla.

Define la función biseccion(f,a,b, epsilon) que aplica la función bolzano() y las funciones cortar_inf() y cortar_sup() reiteradamene hasta conseguir un intervalo de longitud menor que $\varepsilon$. Entonces devuelve como valor aproximado $x_{ap}$ el punto medio de ese intervalo. En caso de que $f$ no cumpla la condición de Bolzano en $[a,b]$ la función debe devolver False.

Define la función biseccion_sin(f,a,b, epsilon) sin utilizar las funciones auxiliares bolzano(), cortar_inf() y cortar_sup()

Alternativa: Define la función biseccion(f,a,b,epsilon) que aplica la función bolzano() y las función cortar() reiteradamene hasta conseguir un intervalo de longitud menor que epsilon. Entonces devuelve como valor aproximado $x_{ap}$ el punto medio de ese intervalo. En caso de que $f$ no cumpla la condición de Bolzano en $[a,b]$ la función debe devolver False.

Advertencia: Tened en cuenta que no es lo mismo

izq = -0.5
drch = 1
[izq, drch] = cortar(f, izq, drch)

que

izq = -0.5
drch = 1
izq = cortar(f, izq, drch)[0]
drch = cortar(f, izq, drch)[1]

Con lo primero se llama cortar(f, izq, drch) una sola vez con los valores de izq = -0.5 y drch = 1. Esto es correcto. Con lo segundo se evalua la función cortar(f, izq, drch) dos veces; primero se utilizan los valores de izq = -0.5 y drch = 1 (esto ese correcto) y después se utiliza el valor de izq que se acaba de calcular (esto es incorrecto) y el valor de drch = 1 de la anterior iteración (esto es correcto).

Define la función raiz4_biseccion(a) que calcula la raíz cuarta del número positivo $a$ utilizando la función biseccion() aplicada a $f(x)=x^{4}-a$ en el intervalo $[0,1+a]$ con $\varepsilon=0.0001$. ¿ Cumple $f$ la condición de Bolzano en ese intervalo? ¿Por qué?

Define la función pasos_biseccion(a) que devuelve el número de veces que es necesario aplicar las funciones corte_inf() y corte_sup(), o bien, según el caso, cortar(), al calcular raiz4_biseccion(), es decir, el número de divisiones a la mitad hasta obtener el resultado deseado.

Utiliza las funciones bolzano() y biseccion() para encontrar todas las soluciones de la ecuación $$ x^{3}-5x^{2}-2x+1=0 $$

4.1.4. Método de Newton-Raphson: el caso de la raíz de un número#

Para obtener los valores en los que la gráfica de la función $f(x)$ corta al eje $x$ (es decir los valores de $x$ que verifican $f(x)=0$) se puede obtener una serie de valores que se aproximan a la solución tanto como se quiera. Este es el procedimiento de Newton-Raphson para obtener dicha serie:

se elige un valor inicial $x_0$
el siguiente es $x_1=x_0-\frac{f(x_0)}{f'(x_0)}$
el valor $n+1$ se obtiene a partir del $n:$ $x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$

Supongamos que $x^*$ es una solución de $f(x)=0;$ entonces, se puede probar que dado un valor pequeño arbitrario $\varepsilon,$ podemos encontrar un $m$ tal que si $n>m$ se verifica

\[|x_n - x^*| < \varepsilon\]

El caso de la raíz de un número

Si queremos obtener el cubo de un número $num,$ es decir, queremos encontrar un valor aproximado de $\sqrt[3]{num}$ con error menor que $\varepsilon,$ entonces debemos encontrar los ceros de $f(x)= x^3-num$ con error menor que $\varepsilon.$ En este caso $f'(x)=3x^2.$ Por lo tanto se tiene, con el método de Newton-Raphson, la siguiente sucesión de valores aproximados:

\[ x_{n+1} = x_n-\frac{x_n^3-num}{3x_n^2} \]

En este caso el procedimiento de parada de la búsqueda se obtien con la comprobación:

\[ |x_n^3 - num|<\varepsilon \]

Es decir, cuando se llegue a un valor de $n$ que verifica esa desilgualdad, el valor $x_n$ es un valor aproximado de $\sqrt[3]{num}.$

Explicación geomértica del método

Cunado tenemos un valor de la sución que buscamos, por ejemplo el primero, $x_0,$ el siguiente se obtiene de la siguiente forma. Tomamos el punto de la gráfica de $f,$ $(x_0, f(x_0)),$ y determinamos la recta tangente a la grñafica de $f$ en dicho punto. Entonnces, el punto $x_1$ es la intersección de esa recta tangente con el eje de las $x$’s.

Comprueba que de esta forma se obtiene el valor antes indicado de $x_1$ y el valor antes indicado de $x_{n+1}$ a partir de $x_n.$

Algoritmo babilonio para obtebner un valor paroximado de la raíz cuadrada

Este algortimo, que permite obtener la raíz cuadrada de un número $num,$ es equivalente a obtener el lado de un cuadrado de área $num.$

El procedimiento es como sigue. Se elije un valor inicial $x_0$ y se construye un rectángulo de área $num.$ Si un lado es $x_0$ el otro será $\frac{num}{x_0}.$ El siguinete valor es la media de los lados del anterior rectángulo. Es decir

\[ x_1 = \frac{1}{2}\left(x_0 + \frac{num}{x_0}\right) \]

La idea es que el rectágulo de lados $x_1$ y $num/x_1$ es más “cuadrado” que el que tiene lados $x_0$ y $\frac{num}{x_0}.$ Entonces el valor del término $n+1$ es

\[ x_{n+1} = \frac{1}{2}\left(x_n + \frac{num}{x_n}\right) \]

Es decir todos los rectángulos de lados $x_n$ y $\frac{num}{x_n}$ tienen area $num.$ Pero según $n$ aumenta estos rectángulos son, a cada paso, más “cuadrados”.

Este antiguo procedimiento para calcular raices cuadradas podría ser la idea que generaliza el algoritmo de Newton-Raphson. El algoritmo babolonio se puede ver como un caso particular del de Newton-Raphson cuando $f(x) = x^2 - num.$ Obsérvese que el algoritmo babilonio es muy anterior al de Newton-Raphson.