Resultados

De manera similar a la sección 5.3, consideramos una función de prueba

$$f(x)=\frac{1}{(2\pi)^2} \cos(2\pi x) ,$$

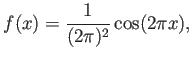
tanto en 1D como en 2D.

Igual que allí, calculamos el error relativo $L_2$ como medida de la convergencia de los métodos, Ec. (5.3). En la figura 7.2 se representa, en escala logarítmica, este error en función del número de nodos, distribuidos al azar en una dimensión. Como se ve, el método FME converge perfectamente. No se puede decir lo mismo del LME, que fracasa de manera bastante evidente. En cambio, el SME sí converge, a pesar de ser sensible, como el LME, al desorden de cada configuración (como queda plasmado en la dispersión de los datos).

Figura 7.2: Convergencia del laplaciano aproximado por los método FME, LME y SME para $N$ partículas al azar en una dimensión. Círculos azules: método FME; cuadrados negros: método SME; cruces verdes: LME.

No parece, por tanto, que en una dimensión compense el esfuerzo que supone la implementación de estos métodos. Por supuesto, la gran esperanza es que en dos dimensiones cambien los resultados, ya que hemos visto que el método FEM no converge. Afortunadamente, parece que esto es así: en la figura 7.3 se muestra cómo, mientras el método FEM no converge en absoluto, el método SME que hemos descrito sí lo hace. Se trata, de hecho, del primer resultado positivo en nuestra búsqueda de métodos de partículas. En esta gráfica se han excluido los resultados del método LME (que no converge) y, para completar la discusión, se han introducido resultados SPH. Estos no convergen, ya que el alcance del kernel se varía como $h=1/\sqrt{N}$ , de modo que el número de vecinos sea, en promedio, siempre el mismo.

Figura 7.3: Convergencia del laplaciano aproximado por los método FME, LME y SME para $N$ partículas al azar en dos dimensiones. Círculos azules: método FME; cuadrados negros: método SME; rombos rojos: SPH.