Operadores diferenciales

Los cálculos resultan ser bastante farragosos (ver apéndice de [1]), pero lo interesante es que este cambio viene dado por magnitudes geométricas bastante intuitivas:

$$\frac{\partial \mathcal{V}_a}{\partial r_b}= \mathcal{A}_{ab} \left( \frac{u_{ab}}{2}- \frac{c_{ab}}{r_{ab}} \right) .$$

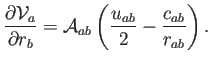
Las expresiones que aparecen en ella son (ver figura 5.1):

• El área (o longitud en 2d) de la cara de Voronoi común a $a$ y $b$ , $\mathcal{A}_{ab}$ .
• La distancia entre $a$ y $b$ , $r_{ab}$ .
• El vector unitario de $a$ hacia $b$ , $u_{ab}$ .
• El vector $c_{ab}$ tiene una definición más complicada: va del punto medio entre $a$ y $b$ hasta el centro de masas de la cara de Voronoi común a $a$ y $b$ . Si el vector $u_{ab}$ es ``radial'', éste sería ``transversal'' o ``de cizalla''.

Figura: Magnitudes geométricas que aparecen en el cambio del volumen de una celda de Voronoi.

Además, si $b=a$ ,

$$\frac{\partial \mathcal{V}_a}{\partial r_b}= - \sum_{b\ne a} \frac{\partial \mathcal{V}_b}{\partial r_a}.$$

Esta propiedad implica que la divergencia de un campo constante será nula; utilizándola, una manera concisa de expresar el operador de la divergencia (4.7) es:

$$\nabla_a \cdot v \doteq \frac{1}{\mathcal{V}_a} \sum_{b\ne a} \ma... ...}}{2} - \frac{\mathbf{c}_{ab}}{R_{ij}} \right] \cdot \left( v_b - v_a \right) .$$ (5.1)

Como se ve, la contribución de la partícula $b$ a $a$ es en todo caso proporcional al área (longitud en 2d) de la cara en contacto común. Luego, hay una parte central de la divergencia, proporcional a $u_{ab}\cdot (v_b-v_a)$ , y una parte transversal proporcional a $u_{ab}\cdot (v_b-v_a)$ .

También puede escribirse la ecuación para el gradiente (4.15) de este modo:

$$\nabla_a p \doteq \frac{1}{\mathcal{V}_a} \sum_{b\ne a} \mathcal{... ...thbf{u}_{ab}}{2} (p_a+p_b) - \frac{\mathbf{c}_{ab}}{R_{ij}} (p_a-p_b) \right] ,$$ (5.2)

donde se ha simetrizado la expresión utilizando el hecho

$$\sum_b \mathcal{A}_{ab} \mathbf{u}_{ab} = 0 ,$$

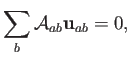
lo cual es fácil de demostrar como una consecuencia del teorema de la divergencia de Gauss aplicado a campos constantes.