Método de Galerkin

Los elementos finitos, definidos arriba, son funciones afines. Sus derivadas son, por tanto, algo patológicas: las primeras serán constantes a trozos (es decir, discontinuas) y las segundas similares a deltas de Dirac (nulas o infinitas, siendo poco rigurosos).

Una manera de regularizar estas derivadas es mediante un método de Galerkin; si bien este método es completamente general y puede emplearse con funciones de cualquier tipo. Nos centramos en las segundas derivadas, sobre todo el laplaciano por ser éste el término que suele ser más delicado en las ecuaciones.

Por ejemplo, tomemos la ecuación de Poisson:

$$\nabla^2 f = g .$$

En el ámbito de las ecuaciones en derivadas parciales, se suele conocer el término de fuente $g$ y el problema es determinar $f$ . En nuestro caso nos preocupamos más bien por una reconstrucción: conocemos $f$ y la tarea es calcular un laplaciano $g$ que cumpla una serie de requisitos. En todo caso, la idea de Galerkin es la misma: introduciendo funciones base $\{s_a\}$ , transferimos el problema de Poisson a lo que denomina una ``forma débil''

$$\int s_a \nabla^2 f = \int g s_a .$$

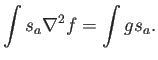
Lo interesante de la idea de Galerkin de reformular el problema en forma débil queda claro si se escribe:

$$\int s_a (\nabla^2 f -g) = 0.$$

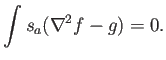
El integrando es el error: $e=\nabla^2 f -g$ , que sería nulo para la solución exacta del problema. Lo que se pretende es, si el error no puede hacerse cero en todo punto, al menos puede ``echarse'' fuera del espacio funcional que se considera, haciendo que sea ortogonal a todas las funciones base. Se encuentran ideas similares en otras áreas del cálculo numérico, por ejemplo en la aproximación mediante polinomios de Chebychev [10].

Si ahora las funciones anteriores se aproximan por

$$f(x)\doteq \sum_a s_a(x) f_a \qquad g(x)\doteq \sum_a s_a(x) g_a$$

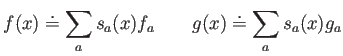
el problema acaba reduciéndose a

$$\sum_b f_b \int s_a \nabla^2 s_b = g_b \int s_a s_b .$$

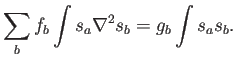
Si ahora aplicamos el teorema de Gauss, despreciando el término de borde (lo cual debe ser debidamente justificado y quizá modificado cerca de las fronteras del dominio):

$$\sum_b \Lambda_{ab} f_b = \sum_b m_{ab} g_b ,$$

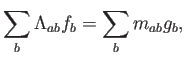
donde la matrix de rigidez es

$$\Lambda_{ab}=- \int (\nabla s_a)\cdot(\nabla s_b)$$

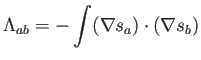
y la matrix de masas es

$$m_{ab}= \int s_a s_b .$$

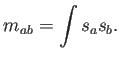
Esta es la formulación habitual del método de Galerkin donde, como se ha dicho, se debe resolver el problema de álgebra lineal

$$\Lambda \vec{f}= m \vec{g},$$

para obtener $f_a$ a partir de $g_a$ .

En nuestra implementación (sección 5.3) el problema es el inverso, más sencillo. Además, planteamos el problema de una manera algo distinta: si definimos el valor de cualquier función en un nodo como

$$g_a=\frac{1}{\int s_a}\int g s_a$$

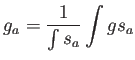
(la división es necesaria para normalizar las funciones peso, si es que no lo están, de tal modo que se cumpla consistencia de orden cero). En este caso, la forma débil pasa a ser

$$\int s_a \nabla^2 f = \int g s_a = g_a \int s_a .$$

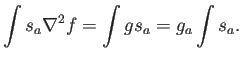
El argumento sigue el mismo cauce, pero la ecuación final es

$$\sum_b \Lambda_{ab} f_b = m'_a g_a ,$$

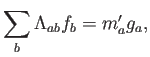
donde la ``matriz'' de masas sería simplemente diagonal, con elementos $m'_a= \int s_a$ . Como casi siempre se satisface consistencia de orden cero, $\sum_b s_b=1$ así que esta reducción de una matriz $m_{ab}$ a otra diagonal $m'_{ab}=m'_a\delta_{ab}$ se llama en este campo ``aproximación de masa acumulada'' (lumped mass approximation). Correspondería a sumar todos los elementos de cada línea de la matriz $m$ y colocar la suma en el elemento diagonal de una matriz diagonal $m'$ . En muchos casos esta aproximación es plausible; en nuestro caso particular es no es tan siquiera una aproximación, sino una consecuencia del planteamiento del problema (ver en todo caso la sección de trabajo futuro 8, donde tendremos algo que decir respecto a esta aproximación.)