Siguiente: Ecuaciones constitutivas Subir: Cambio del momento Anterior: Ecuación de Navier-Stokes Índice General
La energía de una partícula es la suma de energía interna, energía cinética y energía potencial:
Por otro lado, la conservación de la energía viene dada por la primera ley de la termodinámica, que reza:
donde el cambio de energía de una partícula
En cuanto al calor, si se define un flujo de calor por unidad de
área ![]() , de nuevo podemos plantear un problema similar al que relacionaba
fuerza y esfuerzos. Por ejemplo, en la cara
, de nuevo podemos plantear un problema similar al que relacionaba
fuerza y esfuerzos. Por ejemplo, en la cara ![]() izquierda tendremos un
aporte de calor igual a:
izquierda tendremos un
aporte de calor igual a:
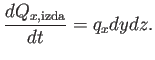
En la dirección
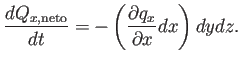
El resultado acaba siendo
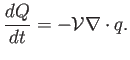
El flujo de calor suele considerarse bien aproximado por la ley de Fourier, que establece que estos flujos son proporcionales al gradiente de temperaturas (y de signo contrario, obviamente):
donde
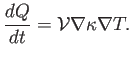
Para el trabajo, el argumento es similar: hay que evaluar la tasa de
trabajo en cada una de las caras. En la cara ![]() izquierda esta tasa
viene dada por la fórmula de la potencia mecánica:
izquierda esta tasa
viene dada por la fórmula de la potencia mecánica:
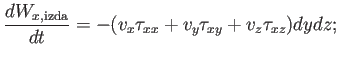
el signo menos se debe a que consideramos el trabajo sobre la partícula de las fuerzas de contacto que aparecían en la ec. (2.6) y siguientes; recordemos que los esfuerzos son positivos en la dirección hacia fuera de la partícula. Así pues, en la dirección
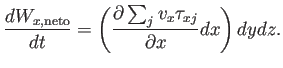
Teniendo en cuenta todas las caras,
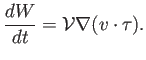
Apliquemos la regla de la cadena:
donde ``
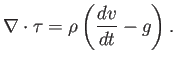
Así pues,
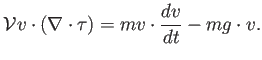
Llega ahora el momento de igualar las dos expresiones para el cambio de energía, y vemos que parte de la ecuación del trabajo cancela la parte de la expresión (2.11) correspondiente al cambio en energía cinética y gravitatoria. El resultado final es:
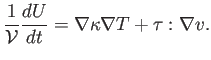
Definiendo la energía interna por unidad de masa
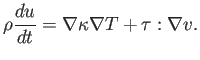
Otra expresión alternativa se puede obtener dividiendo el tensor de esfuerzos en una parte viscosa y otra de presión, diagonal
Entonces,
Pero de la ecuación de continuidad, podemos escribir:
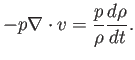
Desarrollando la expresión,
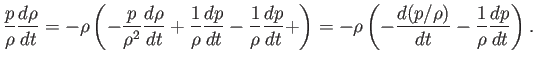
La ecuación de la energía puede reescribirse de este modo:
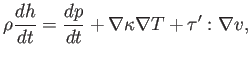
donde la entalpía por unidad de masa es
El término
![]() se denomina ``función de
disipación'', y puede comprobarse que es siempre positivo. Esta
es una expresión de la segunda ley: la viscosidad representa
siempre una pérdida de energía.
se denomina ``función de
disipación'', y puede comprobarse que es siempre positivo. Esta
es una expresión de la segunda ley: la viscosidad representa
siempre una pérdida de energía.
Daniel Duque 2011-11-10