sage: #Adjuntamos el codigo que define grafo_malabar y grafo_malabar_con_cabeza
sage: attach(DATA + 'malabares.sage')
Como vimos, podemos generar trucos de malabares moviéndonos libremente sobre el grafo, sin necesidad de seguir un patrones periódico de siteswap como 441 o 531. Creamos a continuación una animación que cada segundo muestra el estado en que nos encontramos dentro del grafo y el número asociado a la arista que seguimos para llegar al siguiente estado (que es la altura a la que tenemos que lanzar la bola). Cada vez que podemos elegir una arista entre varias posibilidades, escogemos una de las opciones con igual probabilidad.
sage: def camino_aleatorio(g, estado_inicial, longitud=10):
... vs = g.vertices()
... vs.remove(estado_inicial)
... ps = [g.plot(edge_labels=True, layout='circular',
... vertex_size = 400,
... vertex_colors={'blue':[estado_inicial],
... 'white':vs})+
... text('...', (0,0), fontsize=200)]
... v0 = estado_inicial
... for j in xrange(longitud):
... v0,v1,altura = choice(g.outgoing_edges(v0))
... if v1 != v0:
... vs.remove(v1)
... vs.append(v0)
... ps.append(g.plot(edge_labels=True, layout='circular',
... vertex_size = 400,
... vertex_colors={'blue':[v1],
... 'white':vs}) +
... text(altura, (0,0), fontsize=200))
... v0 = v1
... return animate(ps, axes = False, figsize = 8)
sage: g = grafo_malabar(3,5)
sage: #Partimos del estado fundamental
sage: a = camino_aleatorio(g, '***__', longitud = 10)
sage: a.show(delay = 200)
sage: g = grafo_malabar(3,4)
sage: #Partimos del estado fundamental
sage: a = camino_aleatorio(g, '***_', longitud = 10)
sage: a.show(delay = 200)
Si cada vez que lanzamos una bola escogemos la altura entre las posibilidades viables con igual probabilidad, ¿cuánto tiempo pasaremos en cada estado?
Para empezar a entender el problema, trabajamos con 3 bolas y altura 4, y nos planteamos qué pasaría si repetimos el experimento 1000 veces, partiendo por ejemplo del estado fundamental ‘***_’. En el primer lanzamiento, podemos elegir entre hacer un lanzamiento a altura 3 ó 4, de modo que 500 veces estaremos en el estado ‘***_’ y otras 500 en el estado ‘**_*’. Si hacemos dos lanzamientos, tenemos dos decisiones, lo que da lugar a 4 caminos, y seguiremos cada uno de los cuatro en 250 ocasiones. Sin embargo, dos de esos caminos llevan al estado fundamental, luego en 500 ocasiones nos encontramos en ‘***_’, en 250 en ‘**_*’ y en otras 250 en ‘*_**’.
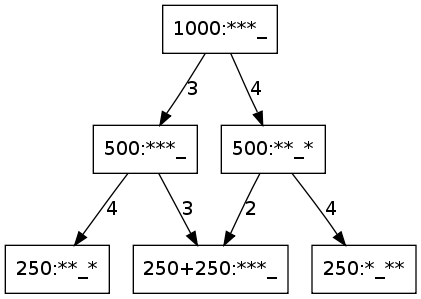
Por supuesto, lo importante no es el número absoluto de lanzamientos, sino la proporción sobre el número de lanzamientos (es decir, 1/2 de las veces nos encontramos en ‘***_’, 1/4 de las veces en ‘**_*’ y el otro 1/4 de las veces en ‘*_**’.). La manera habitual de registrar el experimento anterior en matemáticas es guardar estas proporciones, o probabilidades, en un vector donde guardamos las probabilidades en el orden correspodiente a [‘***_’, ‘**_*’, ‘*_**’, ‘_***’]. En el ejemplo anterior, decimos que estamos en el estado [1/2, 1/4, 1/4, 0]. El estado inicial era el estado determinista [1,0,0,0], y el estado en el primer instante después de empezar era [1/2, 1/2, 0, 0].
Para calcular las probabilidades en un estado a partir de las probabilidades en el anterior, construimos una matriz con las probabilidades de transición a partir de cada estado. Para obtener las probabilidades en un estado a partir de las probabilidades en el anterior, multiplicamos el vector de probabilidades por la matriz de probabilidades de transición.
Esta forma de calcular las transiciones se basa en el teorema de la probabilidad total. La probabilidad de estar en el estado I en tiempo k+1 es igual a la suma para cada estado J del producto de la probabilidad del estado J en tiempo k por la probabilidad de transición de J a I:
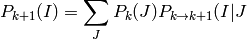
o lo que es lo mismo, juntando en un vector las probabilidades de estar en cada estado ( 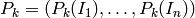 ):
):
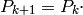
La matriz de probabilidades de transición se obtiene de forma sencilla a partir de la matriz de adyacencia del grafo, que tiene un 1 en la posición (i,j) si hay una flecha del vértice i-ésimo al j-ésimo, y 0 en otro caso.
sage: g = grafo_malabar(3,4)
sage: print g.vertices()
sage: show(g.adjacency_matrix())
sage: M = matrix([row/sum(row) for row in g.adjacency_matrix().rows()])
sage: show(M)
['***_', '**_*', '*_**', '_***']

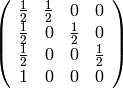
Calculamos el vector de probabilidades hasta después de 10 instantes.
sage: print g.vertices()
sage: M = matrix([row/sum(row*M) for row in g.adjacency_matrix().rows()])
sage: # Partiendo de un estado inicial [1,0,...0])
sage: estado = vector( [1]+[0]*(len(g.vertices())-1) )
sage: n3 = lambda x: x.n(digits = 3)
sage: for k in range(10):
... print k, ':', map(n3, estado)
... estado = estado*M
['***_', '**_*', '*_**', '_***']
0 : [1.00, 0.000, 0.000, 0.000]
1 : [0.500, 0.500, 0.000, 0.000]
2 : [0.500, 0.250, 0.250, 0.000]
3 : [0.500, 0.250, 0.125, 0.125]
4 : [0.562, 0.250, 0.125, 0.0625]
5 : [0.531, 0.281, 0.125, 0.0625]
6 : [0.531, 0.266, 0.141, 0.0625]
7 : [0.531, 0.266, 0.133, 0.0703]
8 : [0.535, 0.266, 0.133, 0.0664]
9 : [0.533, 0.268, 0.133, 0.0664]
Mostramos la información de modo gráfico: en la siguiente animación mostramos la probabilidad como tonalidad de azul: mayor tonalidad de azul corresponde a mayor probabilidad. Comenzamos con el estado fundamental completamente azul y todos los demás blancos, lo que corresponde a que estamos en el estado fundamental con total seguridad (con probabilidad 1), pero en cada instante de tiempo cada nodo bifurca la mitad de su probabilidad (su “cantidad de azul”) a todos los estados a los que se puede acceder desde este en un solo paso.
sage: def cadena_de_Markov(g, prob_inicial, longitud=10):
... vs = g.vertices()
... probs = vector(prob_inicial[v] for v in vs)
... ps = [g.plot(edge_labels=True, layout='circular',
... vertex_size = 400,
... vertex_colors=dict(((1-p,1-p,1-0.001*random()),[v])
... for v,p in zip(vs,probs)))+
... text(map(n3,probs), (0,-1.2), fontsize=20)]*2
... M = matrix([row/sum(row) for row in g.adjacency_matrix().rows()])
...
... for j in xrange(longitud):
... probs = probs*M
... ps.append(g.plot(edge_labels=True, layout='circular',
... vertex_size = 400,
... vertex_colors=dict(((1-p,1-p,1-0.001*random()),[v])
... for v,p in zip(vs,probs)))+
... text(map(n3,probs), (0,-1.2), fontsize=20))
... return animate(ps, axes = False, figsize = 8)
sage: g = grafo_malabar(3,4)
sage: probs = {'***_':1, '**_*':0, '_***':0, '*_**':0, }
sage: a = cadena_de_Markov(g, probs)
sage: a.show(delay = 200)
Repetimos el experimento pero partiendo de un estado inicial distinto.
sage: g = grafo_malabar(3,4)
sage: probs = {'***_':0, '**_*':0, '_***':0, '*_**':1, }
sage: a = cadena_de_Markov(g, probs)
sage: a.show(delay = 200)
Observamos que las probabilidades de transición parecen acercarse al vector [0.533, 0.267, 0.133, 0.0667], y que una vez se llega a ese vector las probabilidades ya no cambian. Para más inri, comprobamos que se llega al mismo vector independientemente del estado inicial.
sage: print g.vertices()
sage: M = matrix([row/sum(row) for row in g.adjacency_matrix().rows()])
sage: # Partiendo de un estado inicial [1,0,...0])
sage: estado = vector( [0,0,1,0])
sage: n3 = lambda x: x.n(digits = 3)
sage: for k in range(10):
... print k, ':', map(n3, estado)
... estado = estado*M
['***_', '**_*', '*_**', '_***']
0 : [0.000, 0.000, 1.00, 0.000]
1 : [0.500, 0.000, 0.000, 0.500]
2 : [0.750, 0.250, 0.000, 0.000]
3 : [0.500, 0.375, 0.125, 0.000]
4 : [0.500, 0.250, 0.188, 0.0625]
5 : [0.531, 0.250, 0.125, 0.0938]
6 : [0.547, 0.266, 0.125, 0.0625]
7 : [0.531, 0.273, 0.133, 0.0625]
8 : [0.531, 0.266, 0.137, 0.0664]
9 : [0.533, 0.266, 0.133, 0.0684]
Pero también podemos observar que para hacer evolucionar un estado k pasos, multiplicamos la distribución de probabilidad por la matriz de transición *k*veces, y esto es equivalente a multiplicar por la matriz 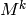 .
.
Observamos que las potencias de la matriz M convergen a una matriz de rango 1, que envía cualquier vector cuyas entradas sumen 1 al mismo vector.
sage: n3 = lambda x: x.n(digits = 3)
sage: show((M).apply_map(n3))
sage: show((M^2).apply_map(n3))
sage: show((M^5).apply_map(n3))
sage: show((M^10).apply_map(n3))
sage: show((M^30).apply_map(n3))
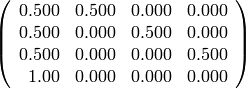
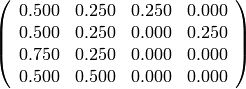



La teoría de cadenas de Markov nos dice que, bajo ciertas hipótesis que verifican todos los grafos que hemos visto, el vector de probabilidades converge siempre a una misma distribución de probabilidad estable, independiente del punto de partida. En los ejercicios exploraremos estas condiciones.
La distribución de probabilidad estable es un autovector por la izquierda de autovalor 1 de la matriz M. Este autovector es único salvo escala. Escogemos el vector tal que la suma de sus componentes es uno.
sage: #el autoespacio asociado a 1 es el nucleo de (M-1)
sage: distribucion_estable = (M - 1).left_kernel().basis()[0]
sage: distribucion_estable /= sum(distribucion_estable)
sage: print g.vertices()
sage: print distribucion_estable
sage: print [n3(p) for p in distribucion_estable]
['***_', '**_*', '*_**', '_***']
(8/15, 4/15, 2/15, 1/15)
[0.533, 0.267, 0.133, 0.0667]
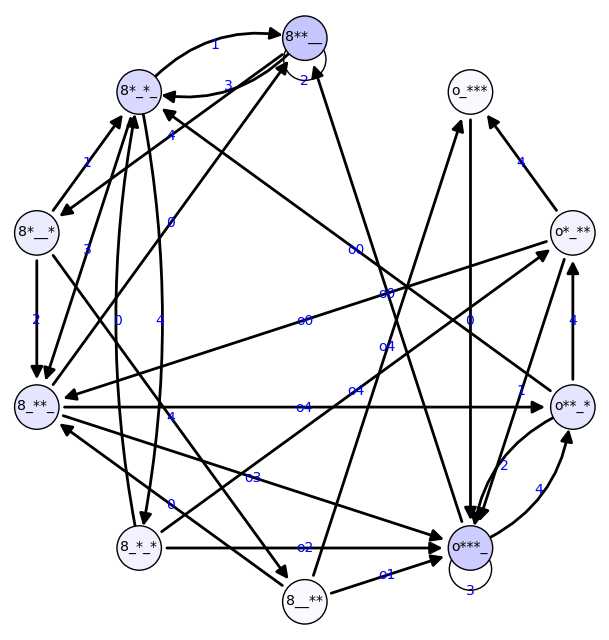
Aplicamos lo anterior al grafo de malabares usando la cabeza. Mostramos sólo la distribución de probabilidad estable.
sage: g = grafo_malabar_con_cabeza(3,4)
sage: vs = g.vertices()
sage: #probs = vector([1/len(g)]*len(g))
sage: M = matrix([row/sum(row) for row in g.adjacency_matrix().rows()])
sage: probs = (M - 1).left_kernel().basis()[0]
sage: probs /= sum(probs)
sage: p = g.plot(edge_labels=True, layout='circular',
... vertex_size = 400,
... vertex_colors=dict(((1-p,1-p,1-0.001*random()),[v])
... for v,p in zip(vs,probs)))
sage: print dict(zip(g.vertices(), map(n3,probs)))
sage: p.show(axes = False, figsize = 8)
{'8__**': 0.0250, 'o**_*': 0.100, '8**__': 0.225, '8_**_': 0.100, '8*__*': 0.0750, 'o_***': 0.0250, '8_*_*': 0.0500, 'o*_**': 0.0500, '8*_*_': 0.150, 'o***_': 0.200}
En general, una cadena de Markov es un sistema en un tiempo discreto, que en cada instante se encuentra en un estado distinto. La cantidad total de estados es finita, y en cada instante se pasa de un estado a otro con unas probabilidades fijas que dependen sólo del estado actual, y no del resto de la historia del sistema.
Es habitual disponer los posibles estados del sistema en un grafo, y poner una arista entre dos vértices i y j cuando el sistema puede evolucionar del estado i al estado j en un sólo instante de tiempo, con probabilidad positiva.
En el caso de los malabares, nos movíamos siempre de un vértice a uno cualquiera de sus vecinos, con igual probabilidad, pero en general no es necesariamente así.
La pregunta que nos hemos hecho (¿cuánto tiempo pasa el sistema en cada estado, a largo plazo?) es la pregunta más típica al estudiar cadenas de Markov.
Como vemos, la probabilidad de estar en cada nodo al cabo de un número grande de iteraciones no depende del estado inicial. Esta probabilidad se puede usar por tanto para medir la importancia de cada nodo (es decir, cómo de bien está conectado). No hay nada en esta idea que sea específico de las malabares, y de hecho esta idea se aplica a grafos de todo tipo.
Por ejemplo, Google afirma que su algoritmo original (el PageRank) para asignar una importancia a cada página web estaba basado en esta idea [1], y antes de eso ya lo habían usado otros, al menos en 1950 [2].
Para poder usarlo en páginas web, tenemos que modificar el algoritmo si de una página no salen links, porque entonces un camino aleatorio que llegue a esa página ya no se mueve. La solución adoptada en google fue que el camino aleatorio, en cualquier momento, puede terminar con probabilidad p, y pasar a otro vértice elegido al azar. Desde sus inicios el algoritmo de google ha sufrido muchas modificaciones, por ejemplo para evitar manipulaciones de páginas web que modificaban sus links para aumentar su ranking.
Los grafos se usan mucho en informática, y a menudo no es necesario añadir etiquetas para obtener información interesante. Por ejemplo, usando un grafo compuesto de usuarios, con aristas que se corresponden a los emails que se envían unos a otros, se puede agrupar a los usuarios por grupos de afinidad.
En 2009, por ejemplo, unos investigadores demostraron que la topología de la red puede ser suficiente para identificar a los usuarios [3]. Es decir, a partir de una red con los nombres de los usuarios y la información de quién era amigo de quien, pudieron poner nombres a los vértices de otra red, en la que sólo tenían los vértices sin nombre, y las aristas correspondientes a esta relación de amistad.
Este es el campo de estudio de la ciencia de las redes [4], que también tiene importantes aplicaciones en ecología, por ejemplo para determinar qué especies son más importantes para la preservación de un cierto ecosistema.
[1] El secreto de Google de Pablo Fernández Gallardo.
[2] http://en.wikipedia.org/wiki/Pagerank#History
[3] http://www.cs.utexas.edu/~shmat/socialnetworks-faq.html
[4] http://en.wikipedia.org/wiki/Complex_network , http://en.wikipedia.org/wiki/Network_science