Estudiaremos finalmente un modelo de la evolución usando cadenas de Markov. Consideramos una única especie, en un entorno estable (incluyendo las otras especies de las que depende). En la población hay una cantidad de genotipos posibles, cada uno de los cuales tiene un fitness 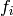 . Si la tasa de mutación no es muy alta, podemos asumir que cuando una mutación aparece, la población evoluciona hasta que esa mutación desaparece, o bien se convierte en el genotipo base, un ancestro común a toda la población. A éste último fenómeno lo llamamos la fijación del nuevo genotipo.
. Si la tasa de mutación no es muy alta, podemos asumir que cuando una mutación aparece, la población evoluciona hasta que esa mutación desaparece, o bien se convierte en el genotipo base, un ancestro común a toda la población. A éste último fenómeno lo llamamos la fijación del nuevo genotipo.
El que ocurra una cosa u otra dependerá del fitness de la mutación y del fitness de la población predominante, amén de otras variables como el tamaño de la población.
Por ejemplo, en un modelo de Moran, tenemos que, si partimos de una población con genotipo predominante i, y aparece un individuo con una mutación, de genotipo j, la probabilidad de fijación del nuevo genotipo j es:
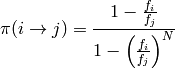
donde 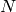 es el tamaño de la población.
es el tamaño de la población.
En el modelo de Wright-Fisher, la probabilidad de fijación del nuevo genotipo es aproximadamente:
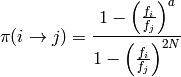
con 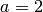 en una población haploidea y
en una población haploidea y 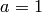 en población diploidea.
en población diploidea.
Vamos a modelizar la evolución de la población con un grafo: a cada genotipo base le asignamos un vértice, y ponemos una arista desde el nodo i al nodo j cuando se puede pasar del genotipo i al j con una sóla mutación. El tiempo es discreto, y la unidad de tiempo incluye varias generaciones, en general un tiempo suficiente como para que el nuevo genotipo se fije con una probabilidad que no sea insignificante. Aunque este parámetro de tiempo es arbitrario, veremos que podemos extraer conclusiones que no dependen de esta elección.
La probabilidad de que el último ancestro común a toda la población pase de ser i a ser j es:
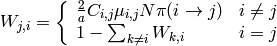
donde 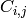 es
es 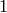 si la distancia de
si la distancia de 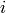 a
a 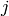 es de 1 mutación, y
es de 1 mutación, y 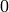 en otro caso,
en otro caso, 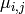 es la tasa de mutación del genotipo
es la tasa de mutación del genotipo 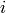 al
al 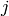 , y el resto ya lo definimos arriba. Si duplicamos la unidad de tiempo, tenemos que duplicar la tasa de mutación. La unidad de tiempo debe ser lo bastante pequeña como para que
, y el resto ya lo definimos arriba. Si duplicamos la unidad de tiempo, tenemos que duplicar la tasa de mutación. La unidad de tiempo debe ser lo bastante pequeña como para que 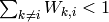 .
.
Sin más información, parece difícil decir mucho más, pero sólo con lo que sabemos, ya podemos responder a alguna pregunta de teoría de evolución.
Uno de los ejercicios consiste en verificar que para este problema existe una única distribución de probabilidad estacionaria.
La distribución de probabilidad estacionaria está dada por la ecuación:
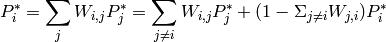
o:
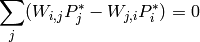
Si la tasa de mutación es simétrica: 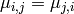 , entonces:
, entonces:
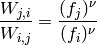
y es fácil verificar que la siguiente distribución de probabilidad es estacionaria:
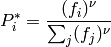
Hemos encontrado la fórmula de la distribución de probabilidad estacionaria. Observa que está dada por una fórmula que no depende de la tasa de mutación, luego el resultado no depende de la elección arbitraria de la unidad de tiempo. De esta fórmula se sigue por ejemplo que:
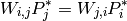
Esto implica que en la historia de la población, se producen tantas mutaciones ventajosas (pasando del genotipo con menor fitness al genotipo con mayor fitness), como al revés, una pregunta de interés para algunas teorías de la evolución. Es decir, aunque es la probabilidad de pasar de un estado a otro más ventojoso es mayor que al revés, como la población pasa una proporción mayor del tiempo en estados más ventajosos, la fijación del fenotipo j partiendo del i se da la misma cantidad de veces que la fijación del fenotipo i partiendo del j.