En este apéndice vamos a aprender el efecto que tienen los ” link farms ” o “mutual admiration societies” en el índice de google. Por supuesto hay otros métodos de link spam más clásicos, pero estudiamos éste método en concreto aprovechando lo que aprendimos sobre cadenas de Markov al hablar de grafos.
El PageRank es un algoritmo abstracto que permite dar un valor numérico ( ranking ) a cada nodo de un grafo que mide de alguna forma su conectividad . Cuantos más links tiene una página web, mayor es su ranking.
Podemos interpretar este ranking de la siguiente forma: cada página web es un nodo de un grafo dirigido, que tiene una arista desde la página A hasta la página B sii en A hay un link que apunta a B. Comenzamos un camino aleatorio en un nodo aleatorio del grafo, escogido con igual probabilidad. Con probabilidad d (el damping factor ), saltamos a uno de sus enlaces, con igual probabilidad. Con probabilidad 1-d, comenzamos desde cero. Hemos construido una cadena de Markov , que a largo plazo tiene una distribución de probabilidad estable que tomamos como ranking de cada nodo: el ranking es la proporción del tiempo que pasamos en ese nodo en el camino aleatorio descrito arriba.
Para más información podéis leer:
http://www.uam.es/personal_pdi/ciencias/gallardo/google.htm
sage: def ranking(g, damping = 0.85):
... #M es la matriz estocastica asociada al grafo
... M = matrix(RDF, [row/sum(row) for row in g.adjacency_matrix().rows()])
... r = M.nrows()
... #T tiene en cuenta el factor de "damping"
... #o la probabilidad de abandonar el camino actual
... #y volver a comenzar desde un nodo aleatorio
... T = damping*M + matrix(RDF, r, [(1 - damping)/r]*(r^2))
...
... #Una aproximacion practica al ranking: tomamos una fila
... #cualquiera de una potencia grande de la matriz
... distribucion_estable = (T^64).rows()[0]
... return dict(zip(g.vertices(),distribucion_estable))
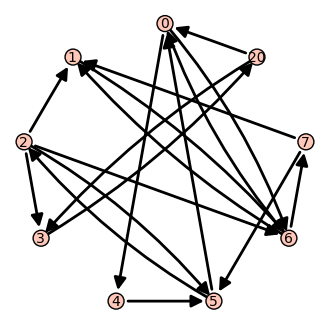
Partimos de un grafo dirigido bastante arbitrario, calculamos el ranking de google de cada nodo, usando el damping por defecto de 0.15.
sage: edges = [(0, 4), (0, 6), (1, 6), (2, 1), (2, 3), (2, 5),
... (2, 6), (3, 1), (3, 2), (3, 5), (3, 6), (4, 5),
... (5, 0), (5, 2), (6, 0), (6, 1), (6, 7), (7, 1),
... (7, 5)]
sage: g=DiGraph(edges)
sage: show(g, layout='circular')
sage: d = ranking(g)
sage: print [(p, v.n(digits = 3)) for p,v in d.items()]
[(0, 0.152), (1, 0.152), (2, 0.0926), (3, 0.0384), (4, 0.0835), (5, 0.154), (6, 0.240), (7, 0.0868)]
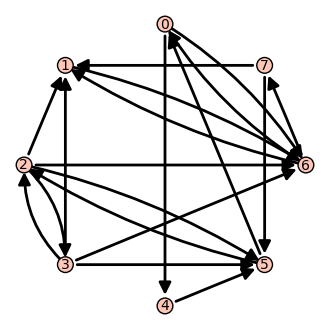
En un primer intento de inflar el ranking del nodo 0, creamos dos nodos, 20 y 21 que apuntan a 0. La táctica apenas es efectiva.
sage: g=DiGraph(edges)
sage: g.add_vertices([20, 21])
sage: g.add_edges([(20,0), (21,0)])
sage: g.show(layout='circular')
sage: d = ranking(g)
sage: print [(p, v.n(digits = 3)) for p,v in d.items()]
[(0, 0.168), (1, 0.139), (2, 0.0848), (3, 0.0330), (4, 0.0866), (5, 0.148), (6, 0.230), (7, 0.0802), (20, 0.0150), (21, 0.0150)]
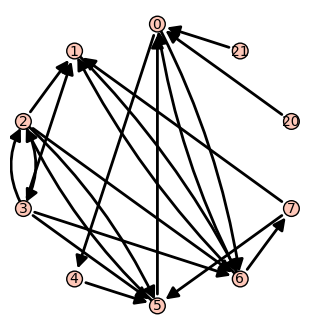
Sin embargo, si desde el vértice 0 tb apuntamos a 20 y 21, la cosa cambia. Ahora los caminos aleatorios que alcanzan 0 se quedan más tiempo orbitando no muy lejos de este nodo.
sage: g=DiGraph(edges)
sage: g.add_vertices([20, 21])
sage: g.add_edges([(0,20), (20,0), (0,21), (21,0)])
sage: g.show(layout='circular')
sage: d = ranking(g)
sage: print [(p, v.n(digits = 3)) for p,v in d.items()]
[(0, 0.224), (1, 0.117), (2, 0.0717), (3, 0.0302), (4, 0.0625), (5, 0.118), (6, 0.184), (7, 0.0671), (20, 0.0625), (21, 0.0625)]
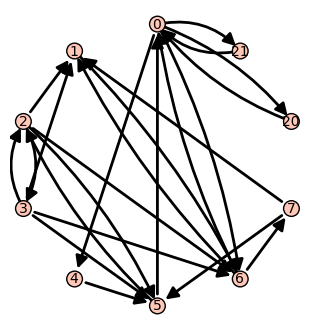
Siguiendo esta misma idea, eliminamos los links “legítimos” del nodo 0. Ahora todos los caminos aleatorios que llegan a 0 pasan su tiempo en circuitos muy cortos que contienen a 0. Los links del nodo 0 a los nodos 4 y 6 permitían que los caminos aleatorios escapasen de la órbita del 0, pero ahora la única manera de salir es que intervenga el factor de damping .
sage: g=DiGraph(edges)
sage: g.add_vertices([20, 21])
sage: g.add_edges([(0,20), (20,0), (0,21), (21,0)])
sage: g.delete_edges([(0,4), (0,6)])
sage: g.show(layout='circular')
sage: d = ranking(g)
sage: print [(p, v.n(digits = 3)) for p,v in d.items()]
[(0, 0.333), (1, 0.0738), (2, 0.0459), (3, 0.0248), (4, 0.0150), (5, 0.0603), (6, 0.0928), (7, 0.0413), (20, 0.157), (21, 0.157)]
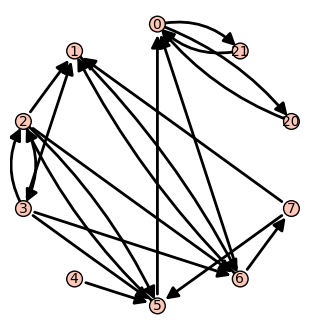
Esta táctica aumenta el ranking de cualquier nodo, pero si era un nodo muy poco conectado tampoco hace milagros. En este caso usamos sólo un nodo extra, el 20, que es más efectivo, y el ranking pasa de 0.04 a 0.16.
sage: g=DiGraph(edges)
sage: g.add_vertices([20])
sage: g.add_edges([(3,20), (20,3)])
sage: g.delete_edges([(3,2), (3,1), (3,5), (3,6)])
sage: g.show(layout='circular')
sage: d = ranking(g)
sage: print [(p, v.n(digits = 3)) for p,v in d.items()]
[(0, 0.111), (1, 0.105), (2, 0.0642), (3, 0.160), (4, 0.0640), (5, 0.112), (6, 0.167), (7, 0.0639), (20, 0.153)]
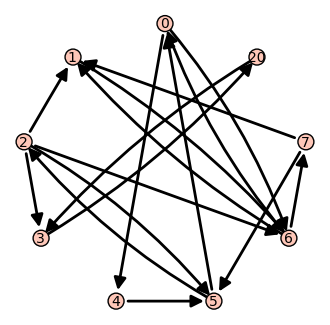
Si la página falsa tiene un link auténtico que aleja el camino aleatorio de nuestro nodo, la técnica se vuelve mucho menos efectiva.
sage: g=DiGraph(edges)
sage: g.add_vertices([20])
sage: g.add_edges([(3,20), (20,3), (20,0)])
sage: g.delete_edges([(3,2), (3,1), (3,5), (3,6)])
sage: g.show(layout='circular')
sage: d = ranking(g)
sage: print [(p, v.n(digits = 3)) for p,v in d.items()]
[(0, 0.163), (1, 0.123), (2, 0.0753), (3, 0.0622), (4, 0.0861), (5, 0.138), (6, 0.207), (7, 0.0753), (20, 0.0696)]