Un autómata celular consiste de:
- un conjunto de celdas, cada una de las cuales puede estar activada, o no. Las celdas se pueden disponer en una línea, una cuadrícula, un grafo.
- una regla de transformación que dice cuál será el estado de una celda en el instante k+1 en función de los estados de las celdas vecinas en el instante k .
Los autómatas celulares se cuentan entre los programas de ordenador más sencillos posibles. La idea de Steven Wolfram es tomar todos los posibles autómatas celulares, sin pensar en qué representan, y estudiar su comportamiento. Algunos de estos autómatas celulares evolucionarán de formas totalmente previsibles, pero otros producen patrones muy intrincados.
sage: %cython
sage: from numpy import zeros
sage: def cellular(rule, int N):
... '''Returns a matrix showing the evolution of a Wolfram's cellular automaton
...
... rule: determines how a cell's value is updated, depending on its neighbors
... N: number of iterations
... '''
... cdef int j,k,numi
... M=zeros( (N,2*N+1), dtype=int)
... M[0,N]=1
...
... for j in range(1,N):
... for k in range(N-j,N+j+1):
... numi = 4*M[j-1,k-1] + 2*M[j-1,k] + M[j-1,k+1]
... M[j,k]=rule[ numi ]
... return M
sage: def plot_rule(rule):
... '''Plots the rule
... '''
... plots = []
... for j in srange(8):
... regla = matrix(2,3)
... digs = j.digits(base=2)
... digs += [0]*(3-len(digs))
... regla[0,0] = digs[2]
... regla[0,1] = digs[1]
... regla[0,2] = digs[0]
... regla[1,1] = rule[j]
... plots.append(matrix_plot(regla, frame=False, figsize=1)+
... line2d([(0,0),(0,2.05),(3,2.05),(3,0),(0,0)],
... thickness=1.5, rgbcolor=(0,0,0), axes=False)+
... line2d([(0,0),(0,2.05),(3,2.05),(3,0),(0,0)],
... thickness=1.5, rgbcolor=(0,0,0), axes=False))
... return html.table([plots])
sage: plot_rule([0,0,0,1,1,0,0,1])

Un número que identifica una regla en la notación de Wolfram, se convierte mediante num2rule en una regla que pueda entender cellular .
El dibujo que realizamos es un matrix_plot , que pone el píxel (i,j) en blanco si la entrada (i,j) de la matriz es 1, y lo pone en negro si la entrada de la matriz es un 0.
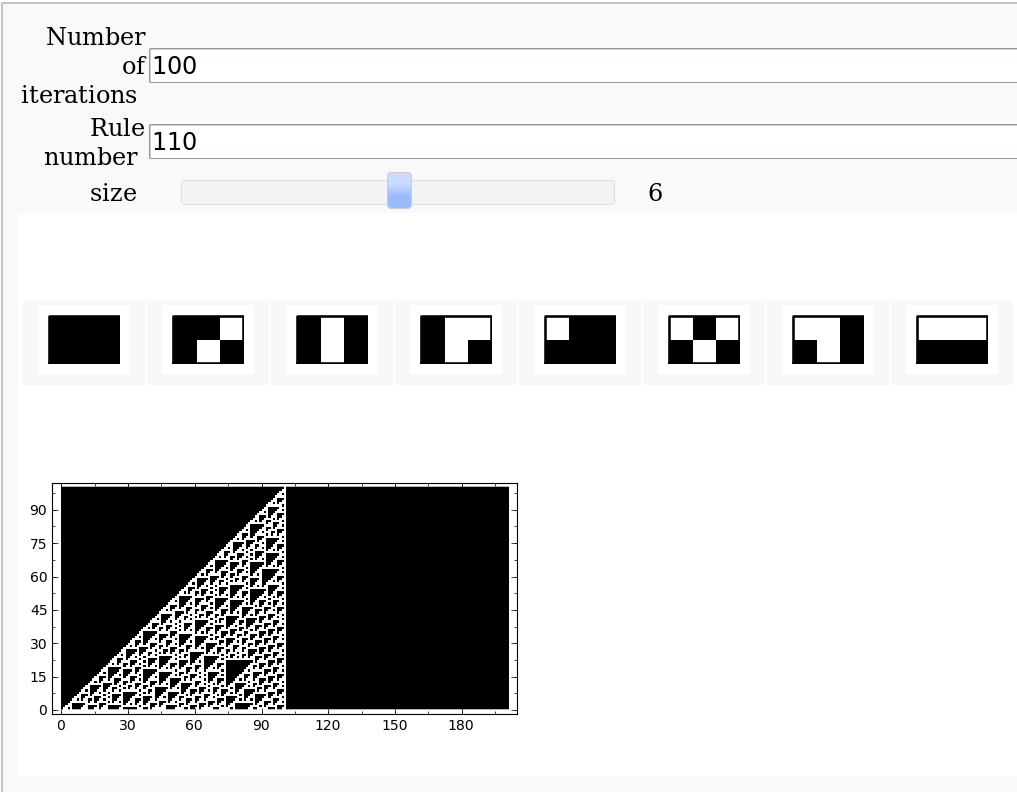
La regla por defecto es la Regla 110 , uno de los automátas celulares más famosos.
sage: def num2rule(number):
... if not (0 <= number <= 255):
... raise Exception('Invalid rule number')
... binary_digits = number.digits(base=2)
... return binary_digits + [0]*(8-len(binary_digits))
sage: @interact
sage: def _( N=input_box(label='Number of iterations',default=100),
... rule_number=input_box(label='Rule number',default=110),
... size = slider(1, 11, step_size=1, default=6 ) ):
... rule = num2rule(rule_number)
... M = cellular(rule, N)
... regla_plot = plot_rule(rule)
... plot_M = matrix_plot(M, axes=False)
... plot_M.show( figsize=[size,size])
http://en.wikipedia.org/wiki/Rule_184
Algunas reglas son modelos de fenómenos del mundo real. En concreto, la regla 184 puede servir como modelo del tráfico en una línea de celdas por donde se mueven los vehículos. Una celda está activa si y sólo si contiene un vehículo. Cada vehículo avanza a la derecha si no hay otro vehículo que se lo impida.
sage: rule184 = num2rule(184)
sage: plot_rule(rule184)

En el ejemplo de debajo, modelizamos dos carreteras que confluyen en una tercera, pasando por un semáforo que se abre alternativamente a una u otra carretera.
sage: l1=30
sage: l2=30
sage: l3=30
sage: turnos=150
sage: #Las tres carreteras
sage: c1 = zero_matrix(ZZ,turnos,l1)
sage: c2 = zero_matrix(ZZ,turnos,l2)
sage: c3 = zero_matrix(ZZ,turnos,l3)
sage: densidad1=0.8
sage: densidad2=0.3
sage: semaforo={1:10,2:10}
sage: abierto=1 #semaforo abierto para c1 0 c2
sage: resto=5
sage: for j in range(turnos):
... #actualizamos el semaforo: restamos un turno y cambiamos al llegar a cero
... resto -= 1
... if resto<=0:
... #cambiamos el semaforo
... abierto=2 if abierto==1 else 1
... #reiniciamos el numero de turnos
... resto = semaforo[abierto]
...
... #actualizamos la carretera 1
... #el primer punto es un 1 o un 0 con probabilidad = densidad1
... c1[j, 0] = 1 if random()<densidad1 else 0
... #el resto, excepto el último, se actualizan con la regla 184
... for k in range(1,l1-1):
... numi = 4*c1[j-1,k-1] + 2*c1[j-1,k] + c1[j-1,k+1]
... c1[j,k] = rule184[numi]
... #actualizamos la carretera 2
... #el primer punto es un 1 o un 0 con probabilidad = densidad2
... c2[j, 0] = 1 if random()<densidad2 else 0
... #el resto, excepto el último, se actualizan con la regla 184
... for k in range(1,l2-1):
... numi = 4*c2[j-1,k-1] + 2*c2[j-1,k] + c2[j-1,k+1]
... c2[j,k] = rule184[numi]
... #actualizamos cerca del semaforo
... if abierto==1:
... numi = 4*c1[j-1,l1-2] + 2*c1[j-1,l1-1] + c3[j-1,0]
... c1[j, l1-1] = rule184[numi]
... numi = 4*c2[j-1,l1-2] + 2*c2[j-1,l1-1] + 1
... c2[j, l1-1] = rule184[numi]
...
... numi = 4*c1[j-1,l1-1] + 2*c3[j-1,0] + c3[j-1,1]
... c3[j, 0] = rule184[numi]
... else:
... numi = 4*c1[j-1,l1-2] + 2*c1[j-1,l1-1] + 1
... c1[j, l1-1] = rule184[numi]
... numi = 4*c2[j-1,l1-2] + 2*c2[j-1,l1-1] + c3[j-1,0]
... c2[j, l1-1] = rule184[numi]
...
... numi = 4*c2[j-1,l1-1] + 2*c3[j-1,0] + c3[j-1,1]
... c3[j, 0] = rule184[numi]
... #actualizamos la carretera 3
... #el resto, excepto el último, se actualizan con la regla 184
... for k in range(1,l3-1):
... numi = 4*c3[j-1,k-1] + 2*c3[j-1,k] + c3[j-1,k+1]
... c3[j,k] = rule184[numi]
... #el ultimo se queda a cero, queriendo decir que sale del sistema
sage: plots=[]
sage: for j in range(turnos):
... c=max(l1,l2)
... M=matrix(ZZ,3,c+l3)
... M[0,(c-l1):c]=c1[j,:]
... M[2,(c-l2):c]=c2[j,:]
... M[1,c:]=c3[j,:]
...
... plots.append(matrix_plot(M, axes=False))
sage: a=animate(plots, axes=False)
sage: a.show()

Exploramos ahora las reglas con tres colores (negro: 0, gris: 1 y blanco: 2) que tienen la siguiente propiedad adicional: el estado de la celda depende sólo de la suma de los colores de las celdas vecinas.
sage: %cython
sage: from numpy import zeros
sage: def cellular2(rule, int N):
... '''Returns a matrix showing the evolution of the totalistic 3-color automaton
...
... rule: determines how a cell's value is updated, depending on its neighbors
... N: number of iterations
... '''
... cdef int j,k,numi
... M=zeros( (N,2*N+1), dtype=int)
... M[0,N]=1
...
... for j in range(1,N):
... for k in range(N-j,N+j+1):
... #color contiene la suma de los tonos de las celdas vecinas
... color = M[j-1,k-1] + M[j-1,k] + M[j-1,k+1]
... M[j,k]=rule[ color ]
... return M
sage: def num2rule2(number):
... if not (0 <= number <= 2186):
... raise Exception('Invalid rule number')
... ternary_digits = number.digits(base=3)
... return ternary_digits + [0]*(7-len(ternary_digits))
sage: @interact
sage: def _cell2( N=input_box(label='Number of iterations',default=100),
... rule_number=input_box(label='Rule number',default=1038),
... size = slider(1, 11, step_size=1, default=6 ) ):
... rule = num2rule2(rule_number)
... M = cellular2(rule, N)
... plot_M = matrix_plot(M)
... plot_M.show( figsize=[size,size])
