En esta sesión vamos a intentar representar distribuciones de probabilidad discretas y continuas y realizar con ellas varias operaciones comunes, como calcular medias y varianzas, hacer extracciones aleatorias según una distribución dada o dibujar las funciones de masa, densidad y distribución. Al final, trabajaremos un poco con variables aleatorias bidimensionales.
Representamos la función de masa mediante un diccionario en el que las claves son los puntos del espacio muestral y el valor asociado a cada clave es la probabilidad de ese punto. Un diccionario representa una distribución de probabilidad si sus valores son números (reales, racionales, incluso expresiones simbólicas) que suman 1.
sage: #Ejemplos:
...
sage: #Bernouilli de prob p=1/3
sage: p = 1/3
sage: f_bernouilli = {0:p, 1:1-p}
sage: #Binomial con prob p=1/3 y k=10 ensayos independientes
sage: k = 10
sage: p = 1/3
sage: f_binomial = dict((j, p^j*(1-p)^(k-j)*binomial(k,j)) for j in range(k+1))
Asumiendo que el espacio muestral está contenido en 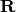 , podemos dibujar la distribución por ejemplo así:
, podemos dibujar la distribución por ejemplo así:
sage: #dibujar una distribucion discreta con soporte finito
sage: def dibuja_f(f, *args, **kargs):
... '''Dibuja una funcion de masa con soporte finito, dada como diccionario
...
... Acepta los argumentos adicionales tipicos de graficas en Sage,
... como color, etc
... '''
... p = (sum([line2d([(x, 0), (x, f[x])], *args, **kargs) for x in f])
... + point2d(f.items(), pointsize=30, *args, **kargs))
...
... #Imponemos rango [0,1] para el eje que muestra las probabilidades
... p.ymin(0)
... p.ymax(1)
... p.axes_labels(['$x$','$p$'])
... return p
sage: show(dibuja_f(f_bernouilli))
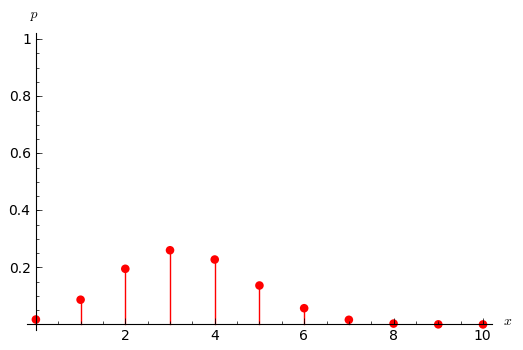
sage: show(dibuja_f(f_binomial, color = (1,0,0)))
De nuevo asumiendo que el espacio muestral está contenido en 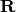 , calculamos la esperanza y la varianza de una variable aleatoria con función de masa f usando las fórmulas habituales:
, calculamos la esperanza y la varianza de una variable aleatoria con función de masa f usando las fórmulas habituales:
![\mu = E[X] = \sum_{i=1}^{N}x_i\:f(x_i)](_images/math/62702c97ff612cdf0c012d4b986800867fe6b9c7.png)
![\sigma^2 = Var[X] = \sum_{i=1}^{N}(x_i - \mu)^2\:f(x_i)](_images/math/1765fc030bb3797378d52219664b550ef51329e7.png)
sage: #media y varianza
sage: def media_f(f):
... return sum(x*f[x] for x in f)
...
sage: def varianza_f(f):
... m = media_f(f)
... return sum((x-m)^2*f[x] for x in f)
sage: print media_f(f_bernouilli), varianza_f(f_bernouilli)
sage: print media_f(f_binomial), varianza_f(f_binomial)
2/3 2/9
10/3 20/9
Como el código anterior es genérico, nada nos impide usar variables simbólicas, y hacer cálculos con parámetros libres.
sage: var('p')
sage: #Bernouilli
sage: #funcion de masa
sage: f = {0:1-p, 1:p}
sage: media_f(f), varianza_f(f)
(p, (p - 1)^2*p - (p - 1)*p^2)
sage: varianza_f(f).factor()
-(p - 1)*p
Para trabajar con la función de distribución, necesitamos ordenar los puntos del espacio muestral. Guardamos en una lista los puntos que tienen probabilidad positiva y en otra lista (del mismo tamaño) la prob de cada punto.
sage: pares = f_binomial.items()
sage: pares.sort()
sage: valores = [x for x,p in pares]
sage: probs = [p for x,p in pares]
sage: cum_probs = []
sage: suma = 0
sage: for p in probs:
... suma += p
... cum_probs.append(suma)
sage: print valores
sage: print probs
sage: print cum_probs
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1024/59049, 5120/59049, 1280/6561, 5120/19683, 4480/19683, 896/6561, 1120/19683, 320/19683, 20/6561, 20/59049, 1/59049]
[1024/59049, 2048/19683, 5888/19683, 11008/19683, 15488/19683, 18176/19683, 2144/2187, 19616/19683, 19676/19683, 59048/59049, 1]
sage: #dibuja la Funcion de distribucion
sage: (point(zip(valores, cum_probs), pointsize=30) +
... sum(line([(valores[j], cum_probs[j]), (valores[j+1], cum_probs[j])])
... for j in range(len(valores)-1)))
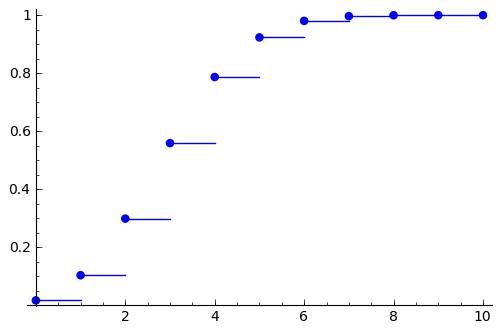
Ejercicio - debate : ¿Cómo podemos extraer un número en el soporte de nuestra función de masa respetando las probabilidades requeridas? Es decir, si tenemos:
f = {0:1/2, 1:1/3, 2:1/6}
valores : [0, 1, 2]
cum_probs : [1/2, 5/6, 1]
queremos una función que devuelva 0 con probabilidad 1/2, 1 con probabilidad 1/3, y 2 con probabilidad 1/6.
Un diccionario no puede contener una cantidad infinita de valores. Para trabajar con distribuciones con soporte infinito podemos usar funciones de python, o expresiones simbólicas. Optamos por la segunda opción para tener al menos la posibilidad de hacer algunos cálculos de forma exacta, aunque no siempre sea posible.
sage: #Geometrica
sage: var('k')
sage: p = 0.1
sage: f_geometrica = (1-p)^k*p
sage: #Probabilidad de que X<=5
sage: print sum(f_geometrica, k, 0, 5).n()
sage: #Poisson de parametro landa = 2
sage: landa = 2
sage: f_poisson = e^(-landa)*landa^k/factorial(k)
sage: #Probabilidad de que X>=3
sage: print sum(f_poisson, k, 3, oo).n()
0.468559000000000
0.323323583816937
sage: #media y varianza
sage: def media_d(f):
... k = f.variables()[0]
... return sum(f*k, k, 0, oo)
...
sage: def varianza_d(f):
... m = media_d(f)
... k = f.variables()[0]
... return sum(f*(k-m)^2, k, 0, oo)
sage: media_d(f_geometrica), varianza_d(f_geometrica)
(9.0, 90.0)
sage: #Alerta BUG: maxima calcula mal la varianza de f_poisson:
sage: #Update 28-04-11: Este bug ha sido corregido en maxima,
sage: #pero la corrección aún tardará un tiempo en llegar a Sage
sage: media_d(f_poisson), varianza_d(f_poisson).n()
(2, 0.812011699419676)
sage: #Sumando unos cuantos terminos tenemos el resultado correcto
sage: sum([f_poisson(k=j)*(j-landa)^2 for j in range(20)]).n()
1.99999999997887
sage: #Sumando por separado tb tenemos el resultado correcto
sage: (sum((e^(-landa)*landa^k/factorial(k))*k^2, k, 0, oo) -
... sum((e^(-landa)*landa^k/factorial(k))*k, k, 0, oo)^2 )
2
sage: #Incluso es capaz de hacerlo con una variable simbolica
sage: #un bug como la copa de un pino!
sage: var('landa')
sage: ( e^(-landa)*sum((landa^k/factorial(k))*(k-landa)^2, k, 0, oo) )
landa
Para dibujar una distribucion discreta con soporte finito, nos conformamos con mostrar unos cuantos puntos que concentran la mayoría de la masa:
sage: def aproxima_df(f, porcentaje_masa = 0.95):
... '''Aproxima una distribucion de probabilidad discreta dada por una
... expresion simbolica por una funcion de masa con soporte finito
... '''
... d = {}
... masa_total = 0
... j = 0
... while masa_total < porcentaje_masa:
... d[j] = f(k = j)
... masa_total += f(k = j)
... j += 1
... return d
sage: def dibuja_d(f, porcentaje_masa = 0.95, *args, **kargs):
... d = aproxima_df(f, porcentaje_masa)
... return dibuja_f(d, *args, **kargs)
sage: dibuja_d(f_geometrica)
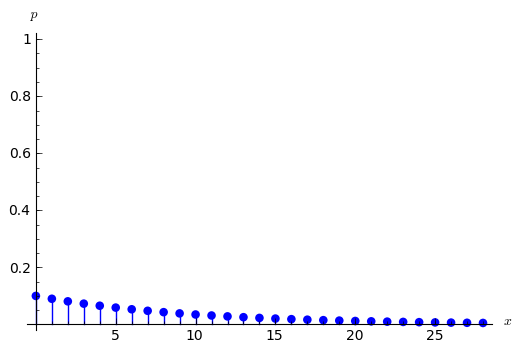
sage: dibuja_d(f_poisson)
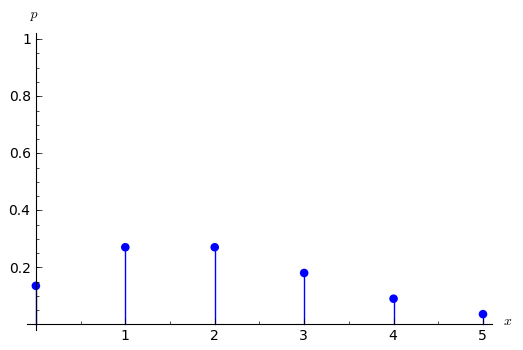
Para extraer un entero con una distribución de probabilidad prescrita, generamos un número aleatorio t entre 0 y 1, y tomamos el menor k tal que la probabilidad acumulada P(X<=k) es mayor que t.
sage: #extraccion aleatoria
sage: def extraccion_aleatoria_d(f):
... t = random()
... j = 0
... prob = f(k=j)
... while prob < t:
... j += 1
... prob += f(k=j)
... return j
sage: extraccion_aleatoria_d(f_geometrica)
1
sage: from collections import defaultdict
sage: T = 1000
sage: frecuencias = defaultdict(int)
sage: for j in range(T):
... k = extraccion_aleatoria_d(f_geometrica)
... frecuencias[k] += 1/T
sage: dibuja_f(frecuencias) + dibuja_d(f_geometrica, 0.99, color=(1,0,0))
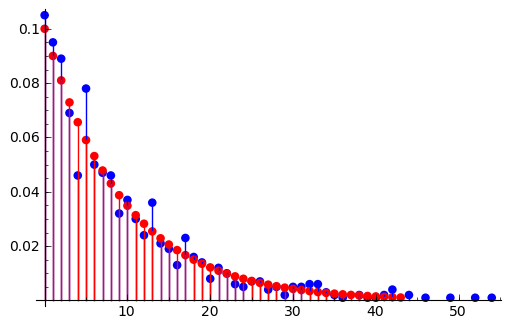
Las distribuciones continuas se pueden manejar de forma similar a las discretas con soporte infinito, pero cambiando sumas por integrales. Por ejemplo, la normal en una variable:
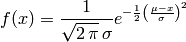
sage: #Distribucion continua
sage: #Normal
sage: #funcion de densidad
sage: var('x')
sage: m = 0.7
sage: s = 1.4
sage: f_normal = (1/sqrt(2*pi*s^2))*e^(-(x - m)^2/(2*s^2))
sage: #Un tipico dibujo de la normal, centrado en la media y con 3
sage: #desviaciones tipicas de rango
sage: show(plot(f_normal, x, m - 3*s, m + 3*s))
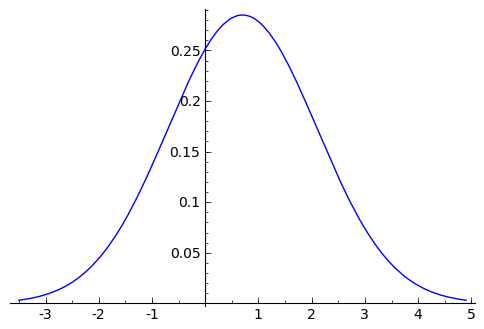
sage: #Probabilidad de que X<1, cuando X~N(0.7, 1.4)
sage: prob, error = numerical_integral(f_normal, -oo, 1)
sage: print prob
sage: #Marcamos en el dibujo la prob pedida
sage: show(plot(f_normal, x, m - 3*s, m + 3*s) +
... plot(f_normal, x, m - 3*s, 1, fill = True))
0.584837871172
sage: #media y varianza
sage: def media_c(f):
... return integral(x*f,x,-oo,oo)
...
sage: def varianza_c(f):
... m = media_c(f)
... return integral((x-m)^2*f,x,-oo,oo)
sage: media_c(f_normal), varianza_c(f_normal)
(0.7, 1.96)
De nuevo, podemos usar variables simbólicas como parámetros.
sage: var('x mu sigma')
sage: assume(sigma > 0)
sage: f_normal = (1/sqrt(2*pi*sigma^2))*e^(-(x - mu)^2/(2*sigma^2))
sage: media_c(f_normal), varianza_c(f_normal)
(mu, sigma^2)
Para hacer extracciones aleatorias de una distribución continua no podemos seguir un procedimiento tan naive como hasta ahora. Tenemos que transformar nuestro número aleatorio, elegido de forma uniforme entre 0 y 1, en un número real (potencialmente entre 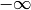 e
e 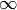 ) que siga una distribución dada X. Por si no lo habéis visto en clase de probabilidad, repasamos el procedimiento habitual brevemente:
) que siga una distribución dada X. Por si no lo habéis visto en clase de probabilidad, repasamos el procedimiento habitual brevemente:
- Queremos generar números x de tal modo que, para cualquier conjunto
, la probabilidad de devolver un número
es exactamente
.
- Comenzamos por elegir un número aleatorio
(es decir, según una distribución uniforme), pero devolvemos el número G(t), para una cierta función G que tenemos que determinar.
- Para cualquier conjunto
, queremos que
tenga medida
. De este modo, la probabilidad de devolver un número
es exactamente
.
- La inversa de la función de distribución
cumple exactamente esta propiedad. Lo comprobamos sólo para intervalos. Si A=[x,y]:
![P(X\in [x,y])=F(y)-F(x)=P(U\in [F(x),F(y)])=P(U\in F([x,y]))=P(U\in G^{-1}([x,y]))](_images/math/1ede6ec5ff630d858f293cdd51372ab69b0f7f0f.png)
sage: #Extraccion aleatoria
sage: m = 0.7
sage: s = 1.4
sage: f_normal = (1/sqrt(2*pi*s^2))*e^(-(x - m)^2/(2*s^2))
sage: #1: extraemos un numero aleatorio entre 0 y 1
sage: t = random()
sage: #2: funcion de distribucion
sage: var('x1')
sage: F_normal = integral(f_normal(x=x1), x1, -oo, x)
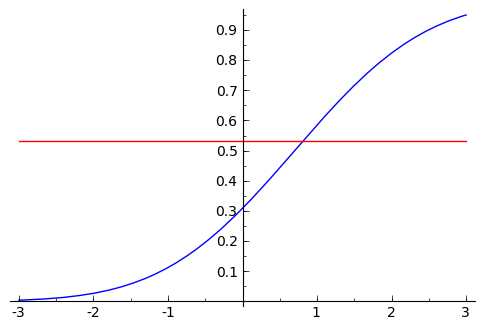
sage: show(plot(F_normal,x,-3,3) +
... plot(0*x+t, x, -3, 3, color=(1,0,0)))
sage: #3: "invertimos" la funcion de distribucion (de forma numerica)
sage: print t, find_root(F_normal - t, m-10*s, m+10*s)
0.531001627926 0.808903109475
sage: #Intentar invertir la funcion de forma simbolica no funciona
sage: #con una normal (puede funcionar en otros casos)
sage: var('p')
sage: solve(F_normal==p, x)
[erf(5/14*sqrt(2)*x - 1/4*sqrt(2)) == 1/4853*(7777*sqrt(2)*p - 4853*e^(1/8))*e^(-1/8)]
sage: #extraccion aleatoria
sage: #el argumento es la funcion de distribucion, no la de densidad
sage: def extraccion_aleatoria_c(F):
... t = random()
... return find_root(F - t, -100, 100)
sage: extraccion_aleatoria_c(F_normal)
0.6299529113987602
Para comparar una muestra aleatoria (una cantidad finita de puntos) con una distribución continua, tenemos que agrupar los datos extraídos en intervalos:
sage: from collections import defaultdict
sage: T = 400
sage: #Dividimos [-K,K] en N partes iguales
sage: K = 3
sage: N = 20
sage: frecuencias = defaultdict(int)
sage: for j in range(T):
... a = extraccion_aleatoria_c(F_normal)
... #TODO: explica las dos lineas siguientes
... k = floor(a*N/(2*K))*(2*K/N)
... frecuencias[k] += 1/(T*2*K/N)
sage: dibuja_f(frecuencias) + plot(f_normal, x, m-3*s, m+3*s, color=(1,0,0))
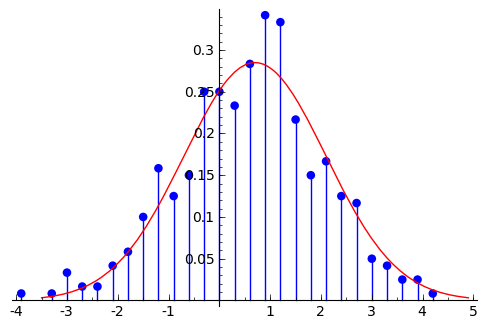
Por supuesto, mucha de esta funcionalidad está incluida en Sage
sage: #extracciones aleatorias de una normal
sage: normalvariate(0,1)
-1.2476798578721822
Las distribuciones en más de una dimensión se manejan de forma similar, pero con más variables simbólicas. Por ejemplo, estudiamos la distribución normal en k dimensiones:
sage: #Normal bidimensional
sage: var('x1 x2')
sage: m1 = 1
sage: m2 = 0
sage: v1 = 3
sage: v12 = -2
sage: v2 = 4
sage: S = matrix(RDF, [[v1,v12],[v12,v2]])
sage: vs = vector([x1,x2])
sage: ms = vector([m1,m2])
sage: f = (1/(2*pi))*(1/sqrt(det(S)))*exp(-(1/2)*(vs-ms)*(~S)*(vs-ms))
sage: #plot3d(f,(x1,-3,3),(x2,-3,3)).show(viewer='tachyon')
sage: p = contour_plot(f, (x1, m1-3*sqrt(v1), m1+3*sqrt(v1)), (x2, m2-3*sqrt(v2), m2+3*sqrt(v2)))
sage: p.show(aspect_ratio=1)
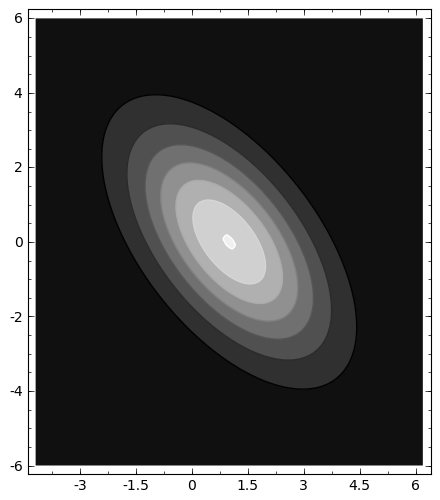
Resolvemos un típico ejercicio de probabilidad condicionada con dos variables normales: X=N(m=0.2,s=0.3) e Y=N(0.5, 0.6) son dos variables aleatorias que siguen una distribución normal, con cov(X,Y)=0.3.
Si sabemos que para un individuo (aka elemento del espacio muestral), Y=1.3, ¿cual es la prob de que X sea mayor que 0.10?
sage: var('x1 x2')
sage: m1 = 0.2
sage: m2 = 0.5
sage: v1 = 0.3
sage: v12 = 0.3
sage: v2 = 0.6
sage: S = matrix(RDF, [[v1,v12],[v12,v2]])
sage: vs = vector([x1,x2])
sage: ms = vector([m1,m2])
sage: f(x1,x2) = (1/(2*pi))*(1/sqrt(det(S)))*exp(-(1/2)*(vs-ms)*(~S)*(vs-ms))
sage: f_marginal_2(x2) = integral(f,x1,-oo,oo)
sage: f_condicionada_1_dado_2(x1,x2) = f(x1,x2)/f_marginal_2(x2)
sage: plot(f_marginal_2,x2, -3, 3)
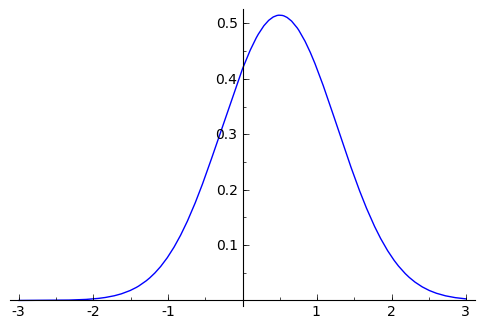
sage: (plot(f_condicionada_1_dado_2(x2=1.3),x1, -3, 3) +
... plot(f_condicionada_1_dado_2(x2=1.3),x1, -3, .1, fill=True))
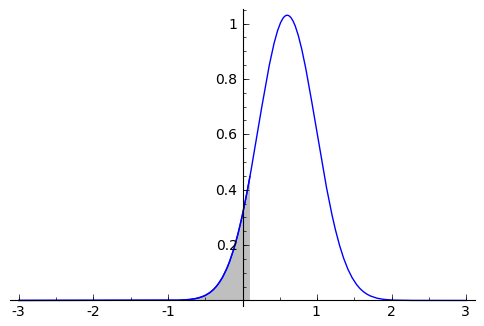
sage: numerical_integral(f_condicionada_1_dado_2(x2=1.3), -oo, 0.1)
(0.098352801229473263, 1.0996705400110192e-08)
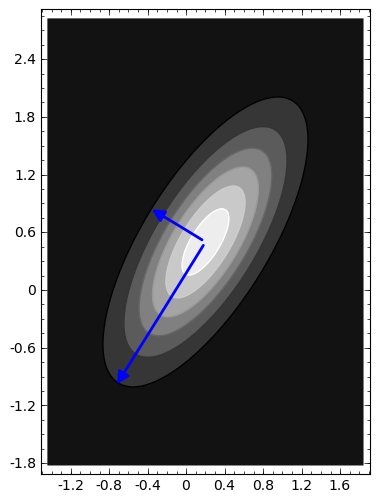
Si diagonalizamos la matriz de varianzas-covarianzas obtenemos variables aleatorias normales e independientes.
sage: S.eigenvectors_left()
[(0.114589803375, [(-0.850650808352, 0.525731112119)], 1), (0.785410196625, [(-0.525731112119, -0.850650808352)], 1)]
sage: [(eval1, [evec1], _ ), (eval2, [evec2], _ )] = S.eigenvectors_left()
sage: p = (contour_plot(f, (x1, m1-3*sqrt(v1), m1+3*sqrt(v1)), (x2, m2-3*sqrt(v2), m2+3*sqrt(v2)))
... + arrow(ms, ms + 2*sqrt(abs(eval1))*evec1)
... + arrow(ms, ms + 2*sqrt(abs(eval2))*evec2))
sage: p.show(aspect_ratio=1)