TeX es el sistema de composición de textos creado por Donald Knuth. TeX, y su extensión LaTeX, desarrollada principalmente por Leslie Lamport, son el sistema más común de escribir textos matemáticos, pues permite incluir fórmulas matemáticas de calidad profesional. El sistema es libre y multiplataforma, y es usado por muchísimos científicos de diversas disciplinas. Existen extensiones que permiten incluir gráficas, notación músical, código de SAGE, y muchas otras cosas.
Al ser un sistema tan extendido, muchos programas utilizan TeX para escribir las matemáticas, como Sage. Cuando editas un bloque de texto, puedes incluir códigos de TeX. Al guardar los cambios, los códigos de TeX se convierten en fórmulas matemáticas. Por mantener la compatibilidad con los tutoriales de TeX, diremos que el texto original, con sus códigos especiales, es el código fuente , y que el resultado final, con las fórmulas matemáticas, es el texto compilado .
Aunque aprender el sistema lleva mucho tiempo, las ideas fundamentales de TeX son sencillas
- Cuando queremos incluir una fórmula matemática dentro de en una línea de texto, la rodeamos con carácteres de $, como por ejemplo: $\sin(\pi)=1$, que se convierte en
al compilar el código. Esta forma de incluir fórmulas se llama en inglés modo inline .
- Cuando queremos incluir una fórmula en su propia línea, la rodeamos con dos caracteres de $. Por ejemplo:
$$e^{\pi i}=-1$$
que se convierte al compilar en:
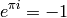
Esta forma de incluir fórmulas se llama en inglés modo display .
Aparte de estas dos formas de incluir fórmulas matemáticas, TeX pone mucho enfásis en la estructura del documento, separándolo en capítulos, secciones, subsecciones... y dentro de ellas teoremas, corolarios, comentarios... Esta parte de TeX no se usa en SAGE, que usa el html para dar estructura al documento. Ambos sistemas, TeX y html, dan mucha importancia a la estructura del documento, y ofrecen al autor la posibilidad de indicar el tipo de contenido en vez de limitarse a colocarlo en la posición correcta con el tamaño de letra deseado.
Lo mejor de SAGE es que podemos obtener fácilmente el código latex que muestra una expresión cualquiera usando el comando latex , que acepta como único argumento un objeto de SAGE, y devuelve su expresión en LaTeX.
sage: var('x')
sage: f=sqrt(x)
sage: print f
sage: show(f)
sage: print latex(f)
sqrt(x)
\sqrt{x}
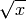
Podemos usar el código latex de arriba en nuestros cuadros de texto: 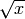 .
.
Veamos más ejemplos:
sage: print latex(pi)
sage: print latex(1/2)
\pi
\frac{1}{2}
El primer ejemplo muestra la forma de introducir las letras griegas: $\alpha$, $\beta$, $\gamma$ se convierten en: 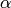 ,
, 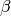 ,
, 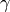 .
.
El segundo ejemplo muestra la forma de escribir fracciones \frac{ numerador }{ denominador }.
Por supuesto, todas los códigos se pueden combinar de cualquier forma:
sage: a=1/sqrt(2*pi)
sage: print a
sage: show(a)
sage: print latex(a)
1/2*sqrt(2)/sqrt(pi)
\frac{1}{2} \, \frac{\sqrt{2}}{\sqrt{\pi}}
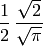
La lista completa de símbolos es enorme, por supuesto, e incluye flechas (\rightarrow: 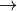 ), operadores (\div:
), operadores (\div: 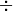 ), desigualdades (\neq:
), desigualdades (\neq: 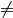 ) ...
) ...
Búsquedas en google arrojan listas bastante completas:
http://omega.albany.edu:8008/Symbols.html
http://stdout.org/~winston/latex/
El siguiente ejemplo usa polinomios.
sage: R1.<t>=PolynomialRing(QQ)
sage: p=t^3-1
sage: print latex(p)
sage: print latex(p/(p+2))
t^{3} - 1
\frac{t^{3} - 1}{t^{3} + 1}
El único comando nuevo es el ^{ superíndice }, para exponentes. El comando equivalente para subíndices es _{ subíndice }. Por ejemplo:
$$x_{1}^{2}+x_{2}^{2}+\dots+x_{n}^{2} $$
se convierte en:
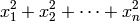
En modo display, y para algunos operadores como el sumatorio (sum) o el límite (limit), los subíndices se muestran debajo del operador:
$$\sum_{j=1}^{N}x_i$$
se convierte en :
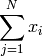
Probamos una función compuesta:
sage: f = sin(x^2)
sage: show(f)
sage: print latex(f)
\sin\left(x^{2}\right)
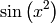
El código de esta función incluye dos nuevos comandos: \left y \right. Estos comandos sirven para cuadrar el paréntesis izquierdo con el derecho, y asegurarse de que son lo bastante grandes para delimitar el contenido.
Siempre que aparece un comando left, debe aparecer después un comando right.
En este caso, después de cada uno hemos usado parétensis, pero podemos poner corchetes o barras verticales:
$$\left[(a+b)^{2}+(a-b)^{2}\right]$$
que se convierte en:
![\left[(a+b)^{2}+(a-b)^{2}\right]](_images/math/794b26e7fcdefd48d0cf41bcb189c3c82ce8e13c.png)
sage: f = sin(1/x)
sage: show(f)
sage: print latex(f)
\sin\left(\frac{1}{x}\right)
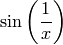
Veamos ahora cómo se muestran matrices:
sage: A=matrix(QQ,[[1,2,3],[4,5,6]])
sage: print A
[1 2 3]
[4 5 6]
sage: show(A)
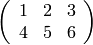
sage: print latex(A)
\left(\begin{array}{rrr}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right)
El contenido entre paréntesis es:
\begin{array}{rrr}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}
El código {rrr} indica que la matriz tiene tres columnas, todas alineadas a la derecha (r:right, l:left, c:center). Los caracteres & delimitan las columnas, y los caracteres \\ delimitan las filas.
copia, pega y modifica el código anterior, para escribir una matriz 2x4 y otra 4x2.
Las fórmulas de la Wikipedia también están escritas en LaTeX. Puedes obtener el código LaTeX que genera una fórmula haciendo click derecho sobre la fórmula y eligiendo “propiedades”, y copiando el “texto alternativo”.
- Copia en esta hoja la fórmula del determinante 3x3 y n x n de la página:
A veces necesitamos sólo uno de los dos paréntesis, corchetes o llaves. Incluso en este caso, escribimos un operador \left y otro \right para delimitar la región, sólo que donde no queremos que ponga un paréntesis, escribimos un punto. Ejemplo:
$$\alpha\left| \frac{1}{2}\right. + \omega\left| \frac{1}{2}\right.$$
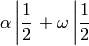
Intenta escribir el código que genera la definición de abajo (no vale mirar):