- Escribe código para recorrer todos los posibles valores de un conjunto de variables x1,x2,...,xK, donde x1 toma los valores 0,1,...,B1-1; x2 toma los valores 0,1,...,B2-1;... y xK toma los valores 0,1,...,BK-1. Los valores B1,..., BK están almacenados en una lista.
- Utiliza el código anterior para contar el número de posibilidades para las que la suma de los valores de las variables es mayor o igual que un número M.
Consideramos matrices 3x3 cuyas entradas son 0 ó 1. El total de matrices de este tipo es 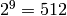 . Cuenta el número de estas matrices cuyo determinante es 1 módulo 2 (es decir, el determinante es impar).
. Cuenta el número de estas matrices cuyo determinante es 1 módulo 2 (es decir, el determinante es impar).
Equivalentemente, cuenta el número de matrices 3x3 con coeficientes en 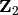 cuyo determinante es no nulo.
cuyo determinante es no nulo.
Encuentra todas las formas de colocar 8 reinas en un tablero de ajedrez de forma que ninguna reina amenace a otra. Plantea el problema como un árbol de soluciones parciales partiendo de un tablero vacío y agregando una sóla reina cada vez. Usa SearchForest para recorrer el grafo.
Nota: el enfoque anterior, tomado de forma literal, da lugar a un algoritmo muy ineficiente. Es buena idea asumir de partida que cada reina tiene que ir en una columna distinta y anotar sólo la fila que ocupa la reina i-ésima.
- Escribe una función genérica que recibe una lista de nodos raices y una función que construye los hijos y devuelva todos los nodos del árbol engendrado (al igual que hicimos con SearchForest), pero realizando una búsqueda en anchura .
- Modifica el código anterior para que devuelva sólo las hojas (nodos que no tienen hijos).
- Aplica esta función a algún ejemplo de la hoja.
Escribe código para recorrer todas las posibles listas que constan de 3 elementos extraídos de una lista dada, en todas las ordenaciones posibles . Usa tres estrategias:
- Usa la función de Sage que extrae listas de tres elementos, y después usa la función de Sage que recorre las permutaciones de las listas de 3 elementos.
- Usa primero la función de Sage que recorre las permutaciones de la lista dada, y después extrae listas de tres elementos que respetan el orden dado.
- Escribe todas las elecciones de sublistas como un árbol cuyo nodo raíz es una sublista vacía, y tal que en cada elección eliges un nuevo elemento de la lista. Nota: recuerda lo que significa un elemento mutable en python!
Nota. Los siguientes problemas de probabilidad se pueden resolver a mano, pero ahora puedes escribir código que utiliza la fórmula:
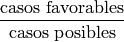
para calcular la probabilidad contando uno por uno los casos favorables.
- Calcula la probabilidad de que, al lanzar 10 monedas (equilibradas), obtengas al menos 4 caras.
- Calcula la probabilidad de que, al lanzar 10 monedas (equilibradas), obtengas el mismo número de caras con las 5 primeras monedas que con las 5 siguientes.
- Calcula la probabilidad de que, al lanzar 15 monedas (equilibradas), las primeras 10 monedas contengan al menos el doble de caras que las 5 monedas siguientes.
Indicación: Usa k variables 0/1 para representar un posible lanzamiento de monedas (1:cara, 0:cruz). Para cada apartado, escribe una función que acepte como argumento una lista con los valores de las variables y devuelva True si es un caso favorable y False si no lo es.
Nos planteamos ahora resolver problemas de cartas. El primer paso es representar las cartas de la baraja. Usaremos la baraja española de 40 cartas para agilizar los cálculos.
Por ejemplo, podemos representar cada carta por una tupla que contiene su número (de 1 a 10, donde 8, 9 y 10 son las figuras) y su palo (por ejemplo, usando la baraja española: ‘o’ (oros), ‘c’ (copas), ‘e’ (espadas), ‘b’ (bastos) ).
- Crea una lista con las 40 cartas de la baraja española, representadas de la forma descrita arriba. Ejemplos: (4,’c’) 4 de copas; (10,’b’) 10 de bastos (rey de bastos).
Para calcular una probabilidad con la fórmula
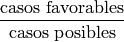
necesitamos, por un lado, recorrer todas las posibles extracciones de cinco cartas de una baraja y, por otro lado, discriminar si una mano de cinco cartas es un caso favorable o no.
- Escribe una función que acepte como argumento una lista con 5 cartas y devuelva True si esa mano es una escalera y False si no lo es.
- Lo mismo de antes, para un póker.
- Calcula la probabilidad de obtener un póker, o una escalera, en la primera mano.
Indicación : si tu código tarda más de unos pocos segundos, será mejor que uses una baraja más pequeña hasta estar seguro de que todo funciona. Ten en cuenta que las posibles extracciones de cinco cartas de una baraja española son 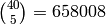 . Usa una baraja con menos palos y menos números, y haz que tu código imprima todos los casos favorables.
. Usa una baraja con menos palos y menos números, y haz que tu código imprima todos los casos favorables.
- Si lo prefieres, calcula la probabilidad de algunas jugadas de mus. Como las manos sólo tienen 4 cartas, hay muchas menos posibilidades.