Algunos problemas de combinatoria requieren gran cantidad de cálculos y se impone una solución con el ordenador. Muchos otros problemas se pueden resolver con papel y lápiz, pero requieren tiempo e ingenio. Sin embargo, escribir programas de ordenador que resuelven los problemas por fuerza bruta suele ser bastante fácil. El problema estriba en que la cantidad de casos a examinar a menudo se dispara, y un programa poco fino sólo podrá resolver los casos más sencillos. A veces, éso es suficiente para darnos una idea, pero en general es más recomendable aprender a hacer programas más eficientes.
En este bloque escribiremos programas que exploran conjuntos de posibilidades muy amplios. Es muy importante comenzar siempre por aplicar nuestros programas con valores muy pequeños, medir bien los tiempos, y sólo lanzar los programas con los valores que nos interesan cuando pensemos que el programa podrá manejarlo.
Comenzamos un truco muy práctico que puede servir como alternativa a anidar muchos bucles for. Supón que tenemos K variables que pueden tomar el valor 0 ó 1, y queremos recorrer todas las posibles combinaciones de valores para cada variable.
Si por ejemplo, K=10, la cantidad total de posibilidades es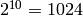 
, algo perfectamente asumible. Anidar 10 bucles es muy poco práctico, y obliga a hacer cambios sustanciales si aumentamos el número de variables:
for k1 in [0,1]:
for k2 in [0,1]:
for k3 in [0,1]:
for k4 in [0,1]:
for k5 in [0,1]:
...
En su lugar, podemos usar el siguiente truco: cuando un número k recorre los números desde 0 hasta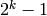 
, sus bits recorren todas las posibles combinaciones de 0 y 1 para K variables. Podemos usar, por ejemplo, el método digits() pasando los argumento base=2 y padto=K , para que extraiga los dígitos binarios (bits) y devuelva siempre listas de longitud K.
Este método lo tienen todos los enteros de SAGE (cuidado: esto nos obliga a usar srange en vez de range , para tener enteros de SAGE en vez de enteros de la máquina).
Con este truco, no necesitamos saber el número de variables al escribir el código.
sage: #Truco para iterar K variables que pueden tomar el valor 0 o 1
sage: #K no es conocido a priori
sage: K=4
sage: for k in srange(2^K):
... vars = k.digits(base=2,padto=K)
... print vars
[0, 0, 0, 0]
[1, 0, 0, 0]
[0, 1, 0, 0]
[1, 1, 0, 0]
[0, 0, 1, 0]
[1, 0, 1, 0]
[0, 1, 1, 0]
[1, 1, 1, 0]
[0, 0, 0, 1]
[1, 0, 0, 1]
[0, 1, 0, 1]
[1, 1, 0, 1]
[0, 0, 1, 1]
[1, 0, 1, 1]
[0, 1, 1, 1]
[1, 1, 1, 1]
La técnica anterior permite iterar sobre todas las sublistas de una lista dada. Dada una lista con k elementos, usamos k variables que pueden tomar los valores 0 y 1. Si la variable xj vale 1, incluimos el elemento j-ésimo en la sublista y, si vale 0, no lo incluimos.
Ejercicio: usa la técnica anterior para mostrar todas las sublistas de una lista dada.
sage: lista = ['a','b','c','d']
También podemos usar la función powerset , definida en SAGE que hace la misma tarea.
sage: for sublista in powerset(lista):
... print sublista
[]
['a']
['b']
['a', 'b']
['c']
['a', 'c']
['b', 'c']
['a', 'b', 'c']
['d']
['a', 'd']
['b', 'd']
['a', 'b', 'd']
['c', 'd']
['a', 'c', 'd']
['b', 'c', 'd']
['a', 'b', 'c', 'd']
¿Cuántos conjuntos de números enteros entre 2 y K tienen máximo común divisor igual a 1?
sage: K = 7
sage: numeros = range(2,K+1)
sage: mcd_es_1 = 0
sage: for subconjunto in powerset(numeros):
... if gcd(subconjunto)==1:
... mcd_es_1 += 1
sage: print mcd_es_1
52
Consideramos el ratio entre el número de conjuntos de números enteros entre 2 y K cuyo máximo común divisor es igual a 1 frente al total de subconjuntos de enteros entre 2 y K: ¿existe el límite de esta sucesión?
sage: probs = []
sage: for K in range(3,15):
... numeros = range(2,K+1)
... mcd_es_1 = 0
... for subconjunto in Subsets(numeros):
... if gcd(subconjunto)==1:
... mcd_es_1 += 1
... total = 2^(K-1)
... probs.append((K,mcd_es_1/total))
sage: point(probs).show(ymin=0,ymax=1)
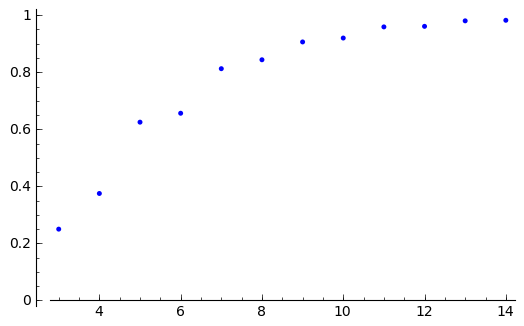
Observación : la función powerset devuelve un objeto similar a un generador. Recordamos que al construir un generador el código no se ejecuta, y no se almacenan en memoria los resultados, sino que sólo se van construyendo según son necesarios, por ejemplo al iterar powerset en un bucle for. Sin embargo, difiere de un generador en que no se agota al iterarlo. Cada vez que recorremos el objeto, se crea un generador nuevo.
sage: ps = powerset([1, 2, 3])
sage: all(1 in s for s in ps)
sage: for k in ps:
... print k
[1]
[2]
[1, 2]
[3]
[1, 3]
[2, 3]
[1, 2, 3]
Los objetos combinatorios suelen admitir una definición recursiva que permite construir unos a partir de otros. Si representamos los objetos primordiales (una lista vacía, un árbol con un sólo nodo ...) como las raíces de un árbol, y utilizamos la definición recursiva para construir las sucesivas generaciones de nodos, podemos generar los objetos de forma bastante limpia, recorriendo el árbol que comienza en cada nodo base (sea en recorrido o en profundidad).
Lo importante de este enfoque es concretar la definición recursiva en una función que acepta un nodo como argumento y devuelve la lista con sus hijos, y separar esta parte de la definición del recorrido del grafo. Para esta segunda parte podemos usar por ejemplo la función SearchForest definida en Sage, que hace un recorrido en profundidad de un bosque, que no es otra cosa que una unión disjunta de árboles. También podemos escribir nuestro propio código genérico para esta tarea.
Como ejemplo, usamos esta idea para construir las particiones de un número k: todas las formas de sumar k con enteros positivos menores que k. Escribimos cada partición de k como una lista de enteros que suma k, y para evitar repeticiones las listamos sólo una vez en orden decreciente. Podemos construir todas las particiones parciales de k, que son listas decrecientes cuya suma es a lo sumo k. Los hijos de una partición parcial L son las particiones parciales que comienzan por L y tienen un elemento más que L. Lo dibujamos como un grafo:
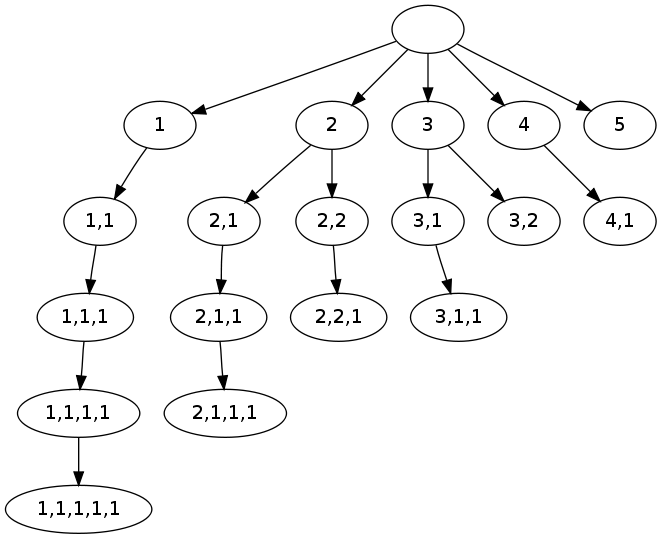
sage: total = 5
sage: def hijos(ls):
... '''Los hijos de una lista ls son las listas que comienzan por ls
... y tienen un elemento más que ls
... '''
... suma = sum(ls)
... minimo = min(ls) if ls else total
... return [ls + [j] for j in range(1, min(total - suma, minimo) + 1)]
sage: hijos([2])
[[2, 1], [2, 2]]
sage: #SearchForest necesita una lista de nodos raices y la funcion que
sage: #genera los hijos
sage: S = SearchForest([[]], hijos)
sage: #Si pasamos el resultado a lista recorremos todas las particiones parciales
sage: [ls for ls in S]
sage: #Si queremos sólo las particiones completas, basta con filtrarlas
sage: [ls for ls in S if sum(ls)==total]
[[1, 1, 1, 1, 1], [2, 1, 1, 1], [2, 2, 1], [3, 1, 1], [3, 2], [4, 1], [5]]
Antes de poder reusar este código, observamos que la función hijos usa la variable total definida en el ámbito principal. Para pasar este código a función, podemos simplemente anidar la función hijos dentro de la nueva función para que pueda acceder al argumento de la función principal:
sage: def particiones(total):
... def hijos(ls):
... suma = sum(ls)
... minimo = min(ls) if ls else total
... return [ls + [j] for j in range(1, min(total - suma, minimo) + 1)]
...
... return [ls for ls in SearchForest([[]], hijos) if sum(ls)==total]
sage: list(particiones(5))
[[1, 1, 1, 1, 1], [2, 1, 1, 1], [2, 2, 1], [3, 1, 1], [3, 2], [4, 1], [5]]
Ya hemos encontrado otros ejemplos de este patrón, como por ejemplo generar todos los polinomios de cierto grado con coeficientes en un cierto rango. Repetimos el ejercicio con esta visión, declarando que los hijos del polinomio p son los polinomios px+j, para j en el rango de coeficientes en el que trabajamos.
sage: m = 3
sage: R.<x> = PolynomialRing(Integers(m))
sage: pols1 = [R(j) for j in srange(m)]
sage: grado_max = 3
sage: def children(p):
... if p.degree()>=grado_max or p == 0:
... return []
... else:
... return [p*x+j for j in srange(m)]
sage: S = SearchForest(pols1, children)
sage: [ls for ls in S]
[0, 1, x, x^2, x^3, x^3 + 1, x^3 + 2, x^2 + 1, x^3 + x, x^3 + x + 1, x^3 + x + 2, x^2 + 2, x^3 + 2*x, x^3 + 2*x + 1, x^3 + 2*x + 2, x + 1, x^2 + x, x^3 + x^2, x^3 + x^2 + 1, x^3 + x^2 + 2, x^2 + x + 1, x^3 + x^2 + x, x^3 + x^2 + x + 1, x^3 + x^2 + x + 2, x^2 + x + 2, x^3 + x^2 + 2*x, x^3 + x^2 + 2*x + 1, x^3 + x^2 + 2*x + 2, x + 2, x^2 + 2*x, x^3 + 2*x^2, x^3 + 2*x^2 + 1, x^3 + 2*x^2 + 2, x^2 + 2*x + 1, x^3 + 2*x^2 + x, x^3 + 2*x^2 + x + 1, x^3 + 2*x^2 + x + 2, x^2 + 2*x + 2, x^3 + 2*x^2 + 2*x, x^3 + 2*x^2 + 2*x + 1, x^3 + 2*x^2 + 2*x + 2, 2, 2*x, 2*x^2, 2*x^3, 2*x^3 + 1, 2*x^3 + 2, 2*x^2 + 1, 2*x^3 + x, 2*x^3 + x + 1, 2*x^3 + x + 2, 2*x^2 + 2, 2*x^3 + 2*x, 2*x^3 + 2*x + 1, 2*x^3 + 2*x + 2, 2*x + 1, 2*x^2 + x, 2*x^3 + x^2, 2*x^3 + x^2 + 1, 2*x^3 + x^2 + 2, 2*x^2 + x + 1, 2*x^3 + x^2 + x, 2*x^3 + x^2 + x + 1, 2*x^3 + x^2 + x + 2, 2*x^2 + x + 2, 2*x^3 + x^2 + 2*x, 2*x^3 + x^2 + 2*x + 1, 2*x^3 + x^2 + 2*x + 2, 2*x + 2, 2*x^2 + 2*x, 2*x^3 + 2*x^2, 2*x^3 + 2*x^2 + 1, 2*x^3 + 2*x^2 + 2, 2*x^2 + 2*x + 1, 2*x^3 + 2*x^2 + x, 2*x^3 + 2*x^2 + x + 1, 2*x^3 + 2*x^2 + x + 2, 2*x^2 + 2*x + 2, 2*x^3 + 2*x^2 + 2*x, 2*x^3 + 2*x^2 + 2*x + 1, 2*x^3 + 2*x^2 + 2*x + 2]
En Sage están definidos muchos objetos combinatorios útiles, que podemos usar y combinar de varias formas. Todos tienen una estructura uniforme que permite usarlos de varias formas. Todas estos objetos combinatorios son perezosos, e incluso podemos definir objetos infinitos. En general usan un método para enumerar todos los objetos y otro distinto para contarlos , que es importante porque en muchos casos se puede contar el número de objetos en muy poco tiempo aplicando fórmulas, mientras que enumerarlos todos podría llevar mucho tiempo. En general, usaremos los siguientes métodos:
- cardinality() para obtener el número de elementos
- list() para obtener la lista de todos los elementos
- random_element() para obtener un elemento aleatorio
- Iteraciones del tipo for objeto in Clase para recorrer los objetos sin necesidad de cargarlos todos en memoria.
Probemos todo ésto con los conjuntos ( Set ) y subconjuntos ( Subsets ) :
sage: S = Set([1,2,3,4])
sage: S1 = Subsets(S)
sage: S1.list()
[{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}]
sage: S2 = Subsets(Subsets(S))
sage: S2.random_element()
{{3}, {4}, {1, 2, 3}, {1, 4}, {}, {2, 3, 4}, {1, 2, 4}, {3, 4}, {1, 3, 4}, {2, 3}, {1, 3}, {2}}
sage: #Por si acaso no te creias que para calcular el cardinal no hace falta
sage: #calcular todos los elementos
sage: S3 = Subsets(Subsets(Subsets(S)))
sage: S3.cardinality()
2003529930406846464979072351560255750447825475569751419265016973710894059556311453089506130880933348101038234342907263181822949382118812668869506364761547029165041871916351587966347219442930927982084309104855990570159318959639524863372367203002916969592156108764948889254090805911457037675208500206671563702366126359747144807111774815880914135742720967190151836282560618091458852699826141425030123391108273603843767876449043205960379124490905707560314035076162562476031863793126484703743782954975613770981604614413308692118102485959152380195331030292162800160568670105651646750568038741529463842244845292537361442533614373729088303794601274724958414864915930647252015155693922628180691650796381064132275307267143998158508811292628901134237782705567421080070065283963322155077831214288551675554073345107213112427399562982719769150054883905223804357045848197956393157853510018992000024141963706813559840464039472194016069517690156119726982337890017641517190051133466306898140219383481435426387306539552969691388024158161859561100640362119796101859534802787167200122604642492385111393400464351623867567078745259464670903886547743483217897012764455529409092021959585751622973333576159552394885297579954028471943529913543763705986928913757153740001986394332464890052543106629669165243419174691389632476560289415199775477703138064781342309596190960654591300890188887588084733625956065444888501447335706058817090162108499714529568344061979690565469813631162053579369791403236328496233046421066136200220175787851857409162050489711781820400187282939943446186224328009837323764931814789848119452713007440220765680910376203999203492023906626264491909167985461515778839060397720759279378852241294301017458086862263369284725851403039615558564330385450688652213114813638408384778263790459607186876728509763471271988890680478243230394718650525660978150729861141430305816927924971409161059417185352275887504477592218301158780701975535722241400019548102005661773589781499532325208589753463547007786690406429016763808161740550405117670093673202804549339027992491867306539931640720492238474815280619166900933805732120816350707634351669869625020969023162859350071874190579161241536897514808261904847946571736601005892476655445840838334790544144817684255327207315586349347605137419779525190365032198020108764738368682531025183377533908861426184800374008082238104076468878471647552945326947661700424461063311238021134588694532200116564076327023074292426051582811070387018345324567635625951430032037432740780879056283663406965030844225855967039271869461158513793386475699748568670079823960604393478850861649260304945061743412365828352144806726676841807083754862211408236579802961200027441324438432402331257403545019352428776430880232850855886089962774458164680857875115807014743763867976955049991643998284357290415378143438847303484261903388841494031366139854257635577105335580206622185577060082551288893332226436281984838613239570676191409638533832374343758830859233722284644287996245605476932428998432652677378373173288063210753211238680604674708428051166488709084770291208161104912555598322366244868556651402684641209694982590565519216188104341226838996283071654868525536914850299539675503954938371853405900096187489473992880432496373165753803673586710175783994818471798498246948060532081996066183434012476096639519778021441199752546704080608499344178256285092726523709898651539462193004607364507926212975917698293892367015170992091531567814439791248475706237804600009918293321306880570046591458387208088016887445835557926258465124763087148566313528934166117490617526671492672176128330845273936469244582892571388877839056300482483799839692029222215486145902373478222682521639957440801727144146179559226175083889020074169926238300282286249284182671243405751424188569994272331606998712986882771820617214453142574944015066139463169197629181506579745526236191224848063890033669074365989226349564114665503062965960199720636202603521917776740668777463549375318899587866282125469797102065747232721372918144666659421872003474508942830911535189271114287108376159222380276605327823351661555149369375778466670145717971901227117812780450240026384758788339396817962950690798817121690686929538248529830023476068454114178139110648560236549754227497231007615131870024053910510913817843721791422528587432098524957878034683703337818421444017138688124249984418618129271198533315382567321870421530631197748535214670955334626336610864667332292409879849256691109516143618601548909740241913509623043612196128165950518666022030715613684732364660868905014263913906515063908199378852318365059897299125404479443425166774299659811849233151555272883274028352688442408752811283289980625912673699546247341543333500147231430612750390307397135252069338173843322950701049061867539433130784798015655130384758155685236218010419650255596181934986315913233036096461905990236112681196023441843363334594927631946101716652913823717182394299216272538461776065694542297877071383198817036964588689811863210976900355735884624464835706291453052757101278872027965364479724025405448132748391794128826423835171949197209797145936887537198729130831738033911016128547415377377715951728084111627597186384924222802373441925469991983672192131287035585307966942713416391033882754318613643490100943197409047331014476299861725424423355612237435715825933382804986243892498222780715951762757847109475119033482241412025182688713728193104253478196128440176479531505057110722974314569915223451643121848657575786528197564843508958384722923534559464521215831657751471298708225909292655638836651120681943836904116252668710044560243704200663709001941185557160472044643696932850060046928140507119069261393993902735534545567470314903886022024639948260501762431969305640666366626090207048887438898907498152865444381862917382901051820869936382661868303915273264581286782806601337500096593364625146091723180312930347877421234679118454791311109897794648216922505629399956793483801699157439700537542134485874586856047286751065423341893839099110586465595113646061055156838541217459801807133163612573079611168343863767667307354583494789788316330129240800836356825939157113130978030516441716682518346573675934198084958947940983292500086389778563494693212473426103062713745077286156922596628573857905533240641849018451328284632709269753830867308409142247659474439973348130810986399417379789657010687026734161967196591599588537834822988270125605842365589539690306474965584147981310997157542043256395776070485100881578291408250777738559790129129407309462785944505859412273194812753225152324801503466519048228961406646890305102510916237770448486230229488966711380555607956620732449373374027836767300203011615227008921843515652121379215748206859356920790214502277133099987729459596952817044582181956080965811702798062669891205061560742325686842271306295009864421853470810407128917646906550836129916694778023822502789667843489199409657361704586786242554006942516693979292624714524945408858422726153755260071904336329196375777502176005195800693847635789586878489536872122898557806826518192703632099480155874455575175312736471421295536494084385586615208012115079075068553344489258693283859653013272046970694571546959353658571788894862333292465202735853188533370948455403336565356988172582528918056635488363743793348411845580168331827676834646291995605513470039147876808640322629616641560667508153710646723108461964247537490553744805318226002710216400980584497526023035640038083472053149941172965736785066421400842696497103241919182121213206939769143923368374709228267738708132236680086924703491586840991153098315412063566123187504305467536983230827966457417620806593177265685841681837966106144963432544111706941700222657817358351259821080769101961052229263879745049019254311900620561906577452416191913187533984049343976823310298465893318373015809592522829206820862230332585280119266496314441316442773003237792274712330696417149945532261035475145631290668854345426869788447742981777493710117614651624183616680254815296335308490849943006763654806102940094693750609845588558043970485914449584445079978497045583550685408745163316464118083123079704389849190506587586425810738422420591191941674182490452700288263983057950057341711487031187142834184499153456702915280104485145176055306971441761368582384102787659324662689978418319620312262421177391477208004883578333569204533935953254564897028558589735505751235129536540502842081022785248776603574246366673148680279486052445782673626230852978265057114624846595914210278122788941448163994973881884622768244851622051817076722169863265701654316919742651230041757329904473537672536845792754365412826553581858046840069367718605020070547247548400805530424951854495267247261347318174742180078574693465447136036975884118029408039616746946288540679172138601225419503819704538417268006398820656328792839582708510919958839448297775647152026132871089526163417707151642899487953564854553553148754978134009964854498635824847690590033116961303766127923464323129706628411307427046202032013368350385425360313636763575212604707425311209233402837482949453104727418969287275572027615272268283376741393425652653283068469997597097750005560889932685025049212884068274139881631540456490350775871680074055685724021758685439053228133770707415830756269628316955687424060527726485853050611356384851965918968649596335568216975437621430778665934730450164822432964891270709898076676625671517269062058815549666382573829274182082278960684488222983394816670984039024283514306813767253460126007269262969468672750794346190439996618979611928750519442356402644303271737341591281496056168353988188569484045342311424613559925272330064881627466723523751234311893442118885085079358163848994487544756331689213869675574302737953785262542329024881047181939037220666894702204258836895840939998453560948869946833852579675161882159410981624918741813364726965123980677561947912557957446471427868624053750576104204267149366084980238274680575982591331006919941904651906531171908926077949119217946407355129633864523035673345588033313197080365457184791550432654899559705862888286866606618021882248602144999973122164138170653480175510438406624412822803616648904257377640956326482825258407669045608439490325290526337532316509087681336614242398309530806549661879381949120033919489494065132398816642080088395554942237096734840072642705701165089075196155370186264797456381187856175457113400473810762763014953309735174180655479112660938034311378532532883533352024934365979129341284854970946826329075830193072665337782559314331110963848053940859283988907796210479847919686876539987477095912788727475874439806779824968278272200926449944559380414608770641941810440758269805688038949654616587983904660587645341810289907194293021774519976104495043196841503455514044820928933378657363052830619990077748726922998608279053171691876578860908941817057993404890218441559791092676862796597583952483926734883634745651687016166240642424241228961118010615682342539392180052483454723779219911228595914191877491793823340010078128326506710281781396029120914720100947878752551263372884222353869490067927664511634758101193875319657242121476038284774774571704578610417385747911301908583877890152334343013005282797038580359815182929600305682612091950943737325454171056383887047528950563961029843641360935641632589408137981511693338619797339821670761004607980096016024823096943043806956620123213650140549586250615282588033022908385812478469315720323233601899469437647726721879376826431828382603564520699468630216048874528424363593558622333506235945002890558581611275341783750455936126130852640828051213873177490200249552738734585956405160830583053770732533971552620444705429573538361113677523169972740292941674204423248113875075631319078272188864053374694213842169928862940479635305150560788126366206497231257579019598873041195626227343728900516561111094111745277965482790471250581999077498063821559376885546498822938985408291325129076478386322494781016753491693489288104203015610283386143827378160946341335383578340765314321417150655877547820252454780657301342277470616744241968952613164274104695474621483756288299771804186785084546965619150908695874251184435837306590951460980451247409411373899927822492983367796011015387096129749705566301637307202750734759922943792393824427421186158236161317886392553095117188421298508307238259729144142251579403883011359083331651858234967221259621812507058113759495525022747274674369887131926670769299199084467161228738858457584622726573330753735572823951616964175198675012681745429323738294143824814377139861906716657572945807804820559511881687188075212971832636442155336787751274766940790117057509819575084563565217389544179875074523854455200133572033332379895074393905312918212255259833790909463630202185353848854825062897715616963860712382771725621313460549401770413581731931763370136332252819127547191443450920711848838366818174263342949611870091503049165339464763717766439120798347494627397822171502090670190302469762151278521956142070806461631373236517853976292092025500288962012970141379640038055734949269073535145961208674796547733692958773628635660143767964038430796864138563447801328261284589184898528048048844180821639423974014362903481665458114454366460032490618763039502356402044530748210241366895196644221339200757479128683805175150634662569391937740283512075666260829890491877287833852178522792045771846965855278790447562192663992008409302075673925363735628390829817577902153202106409617373283598494066652141198183810884515459772895164572131897797907491941013148368544639616904607030107596818933741217575988165127000761262789169510406315857637534787420070222051070891257612361658026806815858499852631465878086616800733264676830206391697203064894405628195406190685242003053463156621891327309069687353181641094514288036605995220248248886711554429104721929134248346438705368508648749099178812670565665387191049721820042371492740164460943459845392536706132210616533085662021188968234005752675486101476993688738209584552211571923479686888160853631615862880150395949418529489227074410828207169303387818084936204018255222271010985653444817207470756019245915599431072949578197878590578940052540122867517142511184356437184053563024181225473266093302710397968091064939272722683035410467632591355279683837705019855234621222858410557119921731717969804339317707750755627056047831779844447637560254637033369247114220815519973691371975163241302748712199863404548248524570118553342675264715978310731245663429805221455494156252724028915333354349341217862037007260315279870771872491234494477147909520734761385425485311552773301030342476835865496093722324007154518129732692081058424090557725645803681462234493189708138897143299831347617799679712453782310703739151473878692119187566700319321281896803322696594459286210607438827416919465162267632540665070881071030394178860564893769816734159025925194611823642945652669372203155504700213598846292758012527715422016629954863130324912311029627923723899766416803497141226527931907636326136814145516376656559839788489381733082668779901962886932296597379951931621187215455287394170243669885593888793316744533363119541518404088283815193421234122820030950313341050704760159987985472529190665222479319715440331794836837373220821885773341623856441380700541913530245943913502554531886454796252260251762928374330465102361057583514550739443339610216229675461415781127197001738611494279501411253280621254775810512972088465263158094806633687670147310733540717710876615935856814098212967730759197382973441445256688770855324570888958320993823432102718224114763732791357568615421252849657903335093152776925505845644010552192644505312073756287744998163646332835816140330175813967359427327690448920361880386754955751806890058532927201493923500525845146706982628548257883267398735220457228239290207144822219885587102896991935873074277815159757620764023951243860202032596596250212578349957710085626386118233813318509014686577064010676278617583772772895892746039403930337271873850536912957126715066896688493880885142943609962012966759079225082275313812849851526902931700263136328942095797577959327635531162066753488651317323872438748063513314512644889967589828812925480076425186586490241111127301357197181381602583178506932244007998656635371544088454866393181708395735780799059730839094881804060935959190907473960904410150516321749681412100765719177483767355751000733616922386537429079457803200042337452807566153042929014495780629634138383551783599764708851349004856973697965238695845994595592090709058956891451141412684505462117945026611750166928260250950770778211950432617383223562437601776799362796099368975191394965033358507155418436456852616674243688920371037495328425927131610537834980740739158633817967658425258036737206469351248652238481341663808061505704829059890696451936440018597120425723007316410009916987524260377362177763430621616744884930810929901009517974541564251204822086714586849255132444266777127863728211331536224301091824391243380214046242223349153559516890816288487989988273630445372432174280215755777967021666317047969728172483392841015642274507271779269399929740308072770395013581545142494049026536105825409373114653104943382484379718606937214444600826798002471229489405761853892203425608302697052876621377373594394224114707074072902725461307358541745691419446487624357682397065703184168467540733466346293673983620004041400714054277632480132742202685393698869787607009590048684650626771363070979821006557285101306601010780633743344773073478653881742681230743766066643312775356466578603715192922768440458273283243808212841218776132042460464900801054731426749260826922155637405486241717031027919996942645620955619816454547662045022411449404749349832206807191352767986747813458203859570413466177937228534940031631599544093684089572533438702986717829770373332806801764639502090023941931499115009105276821119510999063166150311585582835582607179410052528583611369961303442790173811787412061288182062023263849861515656451230047792967563618345768105043341769543067538041113928553792529241347339481050532025708728186307291158911335942014761872664291564036371927602306283840650425441742335464549987055318726887926424102147363698625463747159744354943443899730051742525110877357886390946812096673428152585919924857640488055071329814299359911463239919113959926752576359007446572810191805841807342227734721397723218231771716916400108826112549093361186780575722391018186168549108500885272274374212086524852372456248697662245384819298671129452945515497030585919307198497105414181636968976131126744027009648667545934567059936995464500558921628047976365686133316563907395703272034389175415267500915011198856872708848195531676931681272892143031376818016445477367518353497857924276463354162433601125960252109501612264110346083465648235597934274056868849224458745493776752120324703803035491157544831295275891939893680876327685438769557694881422844311998595700727521393176837831770339130423060958999137314684569010422095161967070506420256733873446115655276175992727151877660010238944760539789516945708802728736225121076224091810066700883474737605156285533943565843756271241244457651663064085939507947550920463932245202535463634444791755661725962187199279186575490857852950012840229035061514937310107009446151011613712423761426722541732055959202782129325725947146417224977321316381845326555279604270541871496236585252458648933254145062642337885651464670604298564781968461593663288954299780722542264790400616019751975007460545150060291806638271497016110987951336633771378434416194053121445291855180136575558667615019373029691932076120009255065081583275508499340768797252369987023567931026804136745718956641431852679054717169962990363015545645090044802789055701968328313630718997699153166679208958768572290600915472919636381673596673959975710326015571920237348580521128117458610065152598883843114511894880552129145775699146577530041384717124577965048175856395072895337539755822087777506072339445587895905719156736L
Dada una lista de tamaño k, las combinaciones de j elementos de la lista son todas las posibles sublistas con j elementos extraídos de la lista. En SAGE, podemos recorrer las combinaciones con un generador, de forma similar a la que usamos para powerset:
for c in Combinations(lista,j):
...haz algo con c...
sage: K=5
sage: for c in Combinations(range(2,K+1),2):
... print c
[2, 3]
[2, 4]
[2, 5]
[3, 4]
[3, 5]
[4, 5]
Ejemplo: ¿Cuál es la probabilidad de que dos números elegidos al azar entre 2 y K sean primos entre sí?
Usando la fórmula:
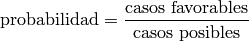
sólo tenemos que extraer todos los posibles pares de números entre 2 y K, y contar cuántas parejas están formadas por dos números primos entre sí.
sage: K=5
sage: primos_relativos = 0
sage: for c in Combinations(range(2,K+1),2):
... if gcd(c)==1:
... primos_relativos += 1
sage: print primos_relativos
5
sage: binomial(10,2)
45
¿Existe el límite cuando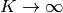 
?
sage: probs = []
sage: for K in range(3,40):
... primos_relativos = 0
... for c in Combinations(range(2,K+1),2):
... if gcd(c)==1:
... primos_relativos += 1
... total = binomial(K-1,2)
... probs.append((K,primos_relativos/total))
sage: print probs
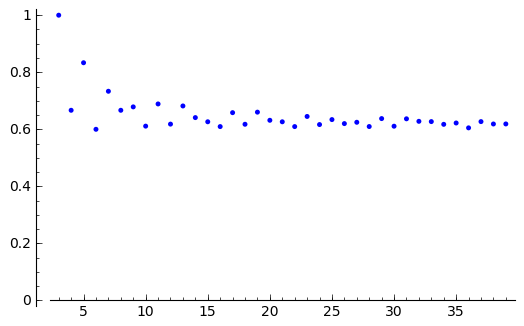
[(3, 1), (4, 2/3), (5, 5/6), (6, 3/5), (7, 11/15), (8, 2/3), (9, 19/28), (10, 11/18), (11, 31/45), (12, 34/55), (13, 15/22), (14, 25/39), (15, 57/91), (16, 64/105), (17, 79/120), (18, 21/34), (19, 101/153), (20, 12/19), (21, 119/190), (22, 64/105), (23, 149/231), (24, 156/253), (25, 175/276), (26, 31/50), (27, 203/325), (28, 214/351), (29, 241/378), (30, 124/203), (31, 277/435), (32, 292/465), (33, 311/496), (34, 163/264), (35, 349/561), (36, 72/119), (37, 79/126), (38, 206/333), (39, 435/703)]
sage: point(probs).show(ymin=0,ymax=1)
- Permutaciones: Permutations(lista) recorre todas las ordenaciones de lista .
- Particiones: Partitions (k) recorre las formas de sumar k con enteros positivos. Además admite argumentos extra para limitar más las particiones (aunque atención: lee bien la documentación porque en algunos casos el resultado no es claro).
- Vectores de enteros: IntegerVectors recorre las formas de sumar un entero con enteros no negativos. También admite argumentos extra.
- WeightedIntegerVectors recorre las formas de sumar un entero usando los enteros de una lista dada (¿de cuántas formas puedo pagar 33 euros usando billetes de 5 y monedas de 2?)
- CartesianProduct calcula el producto cartesiano de dos conjuntos.
sage: Permutations(srange(4)).list()
[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1, 2], [0, 3, 2, 1], [1, 0, 2, 3], [1, 0, 3, 2], [1, 2, 0, 3], [1, 2, 3, 0], [1, 3, 0, 2], [1, 3, 2, 0], [2, 0, 1, 3], [2, 0, 3, 1], [2, 1, 0, 3], [2, 1, 3, 0], [2, 3, 0, 1], [2, 3, 1, 0], [3, 0, 1, 2], [3, 0, 2, 1], [3, 1, 0, 2], [3, 1, 2, 0], [3, 2, 0, 1], [3, 2, 1, 0]]
sage: Partitions(5).list()
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1], [1, 1, 1, 1, 1]]
sage: IntegerVectors(4, max_length=3).list()
[[4], [3, 1], [3, 0, 1], [2, 2], [2, 1, 1], [2, 0, 2], [1, 3], [1, 2, 1], [1, 1, 2], [1, 0, 3], [0, 4], [0, 3, 1], [0, 2, 2], [0, 1, 3], [0, 0, 4]]
sage: #Todas las formas de sumar 8 usando monedas de 1, 2 y 5
sage: WeightedIntegerVectors(8, [1,2,5]).list()
[[1, 1, 1], [3, 0, 1], [0, 4, 0], [2, 3, 0], [4, 2, 0], [6, 1, 0], [8, 0, 0]]
sage: WeightedIntegerVectors(33,[2,5]).list()
[[4, 5], [9, 3], [14, 1]]