Eficiencia en cálculo científico¶

En cálculo ciéntifico, no es raro que ejecutemos un código una sóla vez. Obtenido el resultado, guardamos el código en el archivo y la salida del programa nos responde a una pregunta y nos ayuda a plantear la siguiente. Claramente, no tiene sentido dedicar tiempo a optimizar al máximo un código que probablemente nadie vuelva a usar.

Tenemos que encontrar un equilibrio entre el tiempo que dedicamos a optimizar el programa y el tiempo que podemos esperar a que el código sin optimizar termine. Claramente, nuestro tiempo vale más que el tiempo del ordenador.

La optimización, frecuentemente, también va reñida con otro aspecto muy importante del código científico, la claridad , necesaria para poder compartir nuestro código con la comunidad internacional. Optimizaciones marginales que hacen el código más difícil de seguir (y por tanto, más propenso a esconder errores), no compensan.

PD: Lo anterior se aplica al código exploratorio , que es el más cotidiano en ciencia: un análisis estadístico, una conversión de formato, la solución de una ecuación concreta... pero no al código que forma las librerías en las que se basa el trabajo de mucha gente, porque ese código se va a ejecutar muchas veces en muchos contextos distintos.

Optimiza sólo si es necesario, sólo dónde es necesario¶

Hoy vamos a practicar una metodología típica de lenguajes dinámicos como python:

Escribe código correcto, y claro.

Pruébalo en suficientes casos.

Comprueba si es lo bastante rápido para el tamaño de tus datos. Si lo es, dedícate a otra cosa.

Si el código no es lo bastante rápido, identifica las partes del programa que más influyen en la velocidad (una conocida heurística dice que el 90% del tiempo se pasa ejecutando el 10% del código).

Piensa si tu algoritmo es mejorable y, si puedes, usa otro mejor.

Si tu código no es lo bastante rápido y no conoces mejores algoritmos, reescribe las partes críticas del código en un lenguaje compilado como C, FORTRAN, o cython .

Caso práctico: la constante de Brun¶

Dos números primos p y p+2 se llaman primos gemelos .

La constante de Brun es por definición la suma de los inversos de todos los primos gemelos (y curiosamente se sabe que converge, aunque no se sabe ni siquiera si existen infinitos primos gemelos).

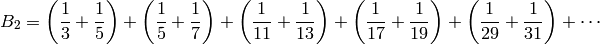
$B_2 = \left(\frac{1}{3} + \frac{1}{5}\right) + \left(\frac{1}{5} + \frac{1}{7}\right) + \left(\frac{1}{11} + \frac{1}{13}\right) + \left(\frac{1}{17} + \frac{1}{19}\right) + \left(\frac{1}{29} + \frac{1}{31}\right) + \cdots$

sage: #Suma de los inversos de los primos gemelos
sage: #1: Encuentra primos
sage: def criba(ls):
...       '''Se queda con los elementos irreducibles de una lista de enteros'''
...       primos = []
...       while ls:
...           p = ls[0]
...           primos.append(p)
...           ls = [k for k in ls if k%p]
...       return primos
sage: def lista_primos(K):
...       'genera los numeros primos menores que K'
...       return criba(range(2,K))
sage: #2: Selecciona los gemelos
sage: #Nos quedamos con el menor de cada par
sage: def criba_gemelos(ls):
...       '''recibe una lista de primos, y devuelve los numeros p tales que
...       p+2 tambien esta en la lista'''
...       return [p for p in ls if p+2 in ls]
sage: #3: Sumamos los inversos
sage: #para aproximar la constante de Brun
sage: def brun(K):
...       '''Devuelve la suma de los inversos de los primos gemelos menores que K'''
...       primos = lista_primos(K)
...       gemelos = criba_gemelos(primos)
...       return sum( (1.0/p + 1.0/(p+2)) for p in gemelos)

sage: %time
sage: print brun(1e4)
1.61689355743220
CPU time: 1.40 s,  Wall time: 1.41 s

La serie converge muy despacio, y si queremos verificar el primer dígito decimal, tenemos que alcanzar al menos 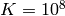$K=10^8$ , lo que claramente nos obliga a optimizar el código.

Aunque con este código tan breve puede ser obvio, vamos a usar una herramienta de profile como ayuda a la metodología de la optimización progresiva. La herramienta nos ayuda a identificar las partes del programa más lentas con menos trabajo que si sólo usamos timeit o similares.

sage: #importamos los modulos cProfile y pstats para ver las estadisticas
sage: #de cuanto tiempo se pasa en cada parte del codigo
sage: import cProfile, pstats
sage: #No necesitamos entender la siguiente linea:
sage: #tomalo como una version avanzada de timeit
sage: cProfile.runctx("brun(10000)", globals(), locals(), DATA + "Profile.prof")
sage: s = pstats.Stats(DATA + "Profile.prof")
sage: #Imprimimos las estadisticas, ordenadas por el tiempo total
sage: s.strip_dirs().sort_stats("time").print_stats()
Tue Feb 22 11:18:44 2011    /home/sageadm/nbfiles.sagenb/home/pang/214/data/Profile.prof

         1446 function calls in 1.371 CPU seconds

   Ordered by: internal time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    1.274    1.274    1.274    1.274 ___code___.py:19(criba_gemelos)
        1    0.095    0.095    0.096    0.096 ___code___.py:4(criba)
      206    0.001    0.000    0.001    0.000 ___code___.py:30(<genexpr>)
        1    0.000    0.000    0.000    0.000 {range}
     1229    0.000    0.000    0.000    0.000 {method 'append' of 'list' objects}
        1    0.000    0.000    0.001    0.001 {sum}
        1    0.000    0.000    0.096    0.096 ___code___.py:13(lista_primos)
        1    0.000    0.000    1.371    1.371 <string>:1(<module>)
        1    0.000    0.000    1.371    1.371 ___code___.py:26(brun)
        1    0.000    0.000    0.001    0.001 functional.py:547(symbolic_sum)
        1    0.000    0.000    0.000    0.000 {hasattr}
        1    0.000    0.000    0.000    0.000 {len}
        1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}


<pstats.Stats instance at 0x433d5f0>

Vemos que la llamada a criba_gemelos es la que ocupa la mayor parte del tiempo. El algoritmo es mejorable: es un algoritmo cuadrático (para cada p de la lista recorremos la lista entera para buscar p+2), cuando para esta tarea podemos usar un algoritmo lineal. Observamos que el primo p+2, si está en la lista, sólo puede estar en un sitio: inmediatamente a continuación del primo p.

sage: #2: Selecciona los gemelos
sage: #Nos quedamos con el menor de cada par
sage: def criba_gemelos(ls):
...       return [ls[j] for j in xrange(len(ls)-1) if ls[j+1]==ls[j]+2]

sage: %time
sage: print brun(1e4)
1.61689355743220
CPU time: 0.12 s,  Wall time: 0.11 s

Pregunta : ¿qué otra forma se te ocurre para reducir la complejidad de criba_gemelos a O(len(ls))?

La mejora es sustancial, y nos planteamos avanzar un orden de magnitud

sage: %time
sage: print brun(1e5)
1.67279958482774
CPU time: 5.69 s,  Wall time: 5.69 s

Como desgraciadamente el resultado sigue siendo insuficiente, volvemos a aplicar el profile para buscar el siguiente fragmento de código que necesita mejoras...

sage: import cProfile, pstats
sage: cProfile.runctx("brun(50000)", globals(), locals(), DATA + "Profile.prof")
sage: s = pstats.Stats(DATA + "Profile.prof")
sage: s.strip_dirs().sort_stats("time").print_stats()
Tue Feb 22 11:18:53 2011    /home/sageadm/nbfiles.sagenb/home/pang/214/data/Profile.prof

         5851 function calls in 1.554 CPU seconds

   Ordered by: internal time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    1.540    1.540    1.541    1.541 ___code___.py:4(criba)
        1    0.008    0.008    0.008    0.008 ___code___.py:4(criba_gemelos)
      706    0.003    0.000    0.003    0.000 ___code___.py:30(<genexpr>)
        1    0.001    0.001    0.001    0.001 {range}
     5133    0.001    0.000    0.001    0.000 {method 'append' of 'list' objects}
        1    0.001    0.001    1.543    1.543 ___code___.py:13(lista_primos)
        1    0.000    0.000    0.003    0.003 {sum}
        1    0.000    0.000    1.554    1.554 <string>:1(<module>)
        1    0.000    0.000    1.554    1.554 ___code___.py:26(brun)
        1    0.000    0.000    0.000    0.000 {hasattr}
        1    0.000    0.000    0.003    0.003 functional.py:547(symbolic_sum)
        2    0.000    0.000    0.000    0.000 {len}
        1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}


<pstats.Stats instance at 0x433df38>

Vemos que ahora sólo compensa dedicarle tiempo a la criba. Comenzamos por estudiar el algoritmo. Algunos de vosotros presentasteis esta otra variante en la práctica, en la que para hallar los primos menores que N mantenemos un array que comienza con todos los números de 1 a N, y cuando descubrimos un número compuesto, lo tachamos poniendo un cero en la posición del array que ocupa.

sage: ##Variante
sage: def lista_primos2(n):
...       aux = [True]*int(n)
...       aux[0] = False
...       aux[1] = False
...
...       for i in xrange(2,floor(sqrt(n))+1):
...           if aux[i]:
...               for j in xrange(i*i,n,i):
...                   aux[j] = False
...
...       ##Devolvemos los que no están tachados
...       return [k for k in xrange(n) if aux[k]]

sage: time b=lista_primos2(1000000)
Time: CPU 0.25 s, Wall: 0.24 s

Aunque podría parecer que ambos algoritmos hacen las mismas operaciones, observamos que:

Con el primer método, intentamos dividir un número por todos los números primos que son menores que su menor factor primo.

Con el segundo método, cada número se tacha varias veces, una por cada factor primo del número.

No necesitamos conocer más detalles, por ahora es suficiente con entender que hacen dos cosas distintas. El segundo método resulta ser mucho más eficiente: (detalles en la wikipedia )

sage: time a=lista_primos(50000)
sage: time b=lista_primos2(50000)
sage: a==b
Time: CPU 1.54 s, Wall: 1.54 s
Time: CPU 0.01 s, Wall: 0.01 s
True

sage: def brun(K):
...       primos = lista_primos2(K)
...       gemelos = criba_gemelos(primos)
...       return sum( (1.0/p + 1.0/(p+2)) for p in gemelos)

sage: %time
sage: print brun(1e5)
1.67279958482774
CPU time: 0.05 s,  Wall time: 0.05 s

sage: %time
sage: print brun(1e6)
1.71077693080422
CPU time: 0.39 s,  Wall time: 0.39 s

El crecimiento aparenta ser casi lineal, y estimamos que podemos tener nuestra respuesta en un tiempo asumible, y pasamos al siguiente problema.

Cython¶

Si estamos usando el mejor algoritmo, o no conocemos otro mejor, y aun así nuestro programa no es lo bastante rápido, podemos compilar las partes críticas del programa.

El lenguaje cython se adapta perfectamente a esta tarea, ya que combina tipos de datos de C con sintaxis de python, de modo que podemos alcanzar mayor velocidad sin tener que reescribir nuestros programas.

Comenzamos con un típico ejemplo numérico, en el que calculamos una integral mediante una suma de Riemann.

sage: def f(x):
...       return sin(x**2)
sage: def integral(a, b, N):
...       dx = (b-a)/N
...       s = 0
...       for i in range(N):
...           s += f(a+dx*i)
...       return s * dx

sage: time integral(0.0, 1.0, 500000)
0.310267460252752
Time: CPU 6.24 s, Wall: 6.26 s

Para compilar una función en cython, comenzamos el bloque de código con %cython .

sage: %cython
sage: #Tenemos que importar la funcion seno
sage: from math import sin
sage: def f(x):
...       return sin(x**2)
sage: def integral_cy1(a, b, N):
...       dx = (b-a)/N
...       s = 0
...       for i in range(N):
...           s += f(a+dx*i)
...       return s * dx

Al ejecutar un bloque de código que comienza por %cython , Sage compila el código , y lo deja listo para llamarlo más adelante como una función normal definida en python.

sage: time integral_cy1(0.0, 1.0, 500000)
0.310267460252752
Time: CPU 2.79 s, Wall: 2.83 s

Como vemos, el código apenas es un poco más rápido que antes: no hemos indicado los tipos de los datos, y en esta situación es imposible hacerlo significativamente mejor que el intérprete de python.

En la siguiente versión le indicamos los tipos de los datos usando la palabra clave cdef : int o float .

sage: %cython
sage: from math import sin
sage: def f(double x):
...       return sin(x**2)
...
sage: def integral_cy2(double a, double b, int N):
...       cdef double dx = (b-a)/N
...       cdef int i
...       cdef double s = 0
...       for i in range(N):
...           s += f(a+dx*i)
...       return s * dx

sage: time integral_cy2(0.0, 1.0, 500000)
0.31026746025275187
Time: CPU 0.10 s, Wall: 0.10 s

La estrategia anterior (compilar en cython indicando los tipos de los datos) se suele poder aplicar de forma bastante mecánica y da resultados interesantes. En general, es posible optimizar el código todavía más, pero hace falta conocimiento más específico y por tanto más difícil de aplicar en cada caso concreto. A modo de referencia, veamos el siguiente código:

sage: %cython
sage: #Usamos la funcion seno directamente de la libreria
sage: #"math.h" de C
sage: cdef extern from "math.h": # external library
...       double sin(double)
sage: #Las funciones definidas con cdef solo son accesibles
sage: #desde codigo cython, pero son mas rapidas
sage: cdef double f(double x):
...       return sin(x**2)
sage: def integral_cy3(double a, double b, int N):
...       cdef double dx = (b-a)/N
...       cdef int i
...       cdef double s = 0
...       for i in range(N):
...           s += f(a+dx*i)
...       return s * dx

sage: time integral_cy3(0.0, 1.0, 500000)
0.31026746025275187
Time: CPU 0.02 s, Wall: 0.02 s

El conjunto de Mandelbrot¶

El conjunto de Mandelbrot es el subconjunto de los números complejos formados por aquellos números c tales que las iteraciones de la regla 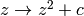$z\rightarrow z^2+c$ comenzando en 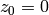$z_0=0$ permanecen acotadas.

Como aproximación, es habitual tomar un punto c del plano complejo e iterar la regla anterior hasta que se abandona una bola de un cierto radio, o se alcanza un cierto número de iteraciones.

Comenzamos con un programa en python puro.

Dividimos el cuadrado del plano complejo con vértices $(x_0,y_0)$ , $(x_0+l,y_0)$ , $(x_0+l,y_0+l)$ y $(x_0,y_0+l)$ en una malla NxN.

En la posición (j,k) de un array NxN almacenamos el número de iteraciones h necesarias para que $z_h$ abandone una bola de radio R cuando comenzamos a iterar $z\rightarrow z^2+c$ partiendo del punto $c=(x_0+j\:l/N) + i(y_0+k\:l/N)$ .

sage: def mandelbrot(x0, y0, side, N=200, L=50, R=float(3)):
...       m=matrix(N,N)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = complex(x0+j*delta,y0+k*delta)
...               z=0
...               h=0
...               while (h<L) and (abs(z)<R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m

sage: time m=mandelbrot(-2,-1.5,3,100,20)
sage: matrix_plot(m)
Time: CPU 0.65 s, Wall: 0.67 s

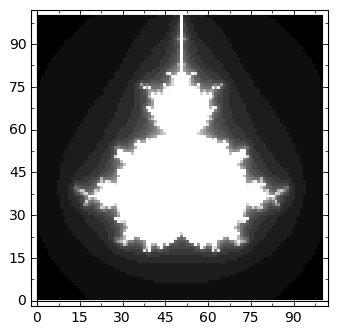
Nuestro código es una traslación bastante literal de la definición, y sin saber ninguna propiedad especial del conjunto no parece haber forma de sustituir el algoritmo. Usamos el lenguaje cython.

sage: %cython
sage: def mandelbrot_cy_1(x0, y0, side, N=200, L=50, R=float(3)):
...       m=matrix(N,N)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = complex(x0+j*delta,y0+k*delta)
...               z=0
...               h=0
...               while (h<L) and (abs(z)<R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m


Error converting Pyrex file to C:
------------------------------------------------------------
...
include "interrupt.pxi"  # ctrl-c interrupt block support
include "stdsage.pxi"  # ctrl-c interrupt block support

include "cdefs.pxi"
def mandelbrot_cy_1(x0, y0, side, N=200, L=50, R=float(3)):
    m=matrix(N,N)
           ^
------------------------------------------------------------

/home/sageadm/.sage/temp/sageserver/23963/spyx/_home_sageadm_nbfiles_sagenb_home_pang_214_code_sage35_spyx/_home_sageadm_nbfiles_sagenb_home_pang_214_code_sage35_spyx_0.pyx:7:12: undeclared name not builtin: matrix
Traceback (most recent call last):
...
RuntimeError: Error converting /home/sageadm/nbfiles.sagenb/home/pang/214/code/sage35.spyx to C:

Al tratar de compilar el código, obtenemos un error:

undeclared name not builtin: matrix

que nos indica que tenemos que importar el constructor de matrices ( matrix ) de la librería correspondiente. Encontramos la ruta requerida para importar en la ayuda de matrix, más concretamente en la primera línea, que indica el fichero en que se define matrix .

sage: matrix?
<html>...</html>

sage: %cython
sage: from sage.matrix.constructor import matrix
sage: def mandelbrot_cy_1(x0, y0, side, N=200, L=50, R=float(3)):
...       m=matrix(N,N)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = complex(x0+j*delta,y0+k*delta)
...               z=0
...               h=0
...               while (h<L) and (abs(z)<R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m

sage: time m=mandelbrot_cy_1(-2,-1.5,3,200,50)
Time: CPU 1.88 s, Wall: 1.89 s

Al ejecutar un bloque de código que comienza por %cython , Sage compila el código , y lo deja listo para llamarlo más adelante como una función normal definida en python. También genera un informe en html que nos permite entender cómo de eficiente es el código generado. Las líneas en amarillo son código que no se ha podido optimizar, y se ejecuta como si fuera código dinámico en python, mientras que las líneas en blanco corresponden a las líneas que se han podido optimizar, y se ejecutan como si fuera código de C. En este primer informe, vemos que casi todas las líneas están en amarillo, porque no hemos indicado los tipos de los datos, y en esta situación es imposible hacerlo significativamente mejor que el intérprete de python.

En la siguiente versión le indicamos los tipos de los datos: int , float o double complex .

sage: %cython
sage: from sage.matrix.constructor import matrix
sage: def mandelbrot_cy2(float x0,float  y0,float side,
...                      int N=200, int L=50, float R=3):
...       '''returns an array NxN to be plotted with matrix_plot
...       '''
...       cdef double complex c, z
...       cdef float delta
...       cdef int h, j, k
...       m=matrix(N,N)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = complex(x0+j*delta,y0+k*delta)
...               z=0
...               h=0
...               while (h<L) and (abs(z)<R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m

sage: time m=mandelbrot_cy2(-2,-1.5,3,200,50)
Time: CPU 0.10 s, Wall: 0.10 s

Indicando los tipos de las variables hemos conseguido una mejora sustancial. Este es un buen momento para detenernos (de hecho, el resto de la sección no entra en el examen).

Optimización en cython más allá de indicar los tipos de datos (opcional)¶

Observando el informe html sobre el código generado, vemos que la condición dentro del bucle while no se está optimizando, y está dentro del bucle más interior, luego es la parte del código que más se repite. El problema es que estamos usando una función abs genérica. Podemos acelerar el cálculo sustituyendo la llamada por operaciones generales sobre números reales (y eliminando la raíz cuadrada implícita al calcular el valor absoluto):

sage: %cython
sage: from sage.matrix.constructor import matrix
sage: def mandelbrot_cy3(float x0,float  y0,float side,
...                      int N=200, int L=50, float R=3):
...       '''returns an array NxN to be plotted with matrix_plot
...       '''
...       cdef double complex c, z
...       cdef float delta
...       cdef int h, j, k
...       m=matrix(N,N)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = complex(x0+j*delta,y0+k*delta)
...               z=0
...               h=0
...               while (h<L and
...                      z.real**2 + z.imag**2 < R*R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m

sage: time m=mandelbrot_cy3(-2,-1.5,3,200,50)
Time: CPU 0.05 s, Wall: 0.06 s

Siguiendo la regla de optimizar sólo la parte que más repite, ponemos el ojo en la línea:

c = complex(x0+j*delta,y0+k*delta)

que aparece en amarillo en el informe, y es interior a dos bucles for. Aunque a veces requeire un poco de ensayo y error, una estrategia que suele funcionar es que las operaciones aritméticas se optimizan cuando declaramos los tipos. Llamadas a funciones como complex no nos dan esas garantías, porque pueden implicar conversiones entre tipos de datos.

sage: %cython
sage: from sage.matrix.constructor import matrix
sage: def mandelbrot_cy4(float x0,float  y0,float side,
...                      int N=200, int L=50, float R=3):
...       '''returns an array NxN to be plotted with matrix_plot
...       '''
...       cdef double complex c, z, I
...       cdef float delta
...       cdef int h, j, k
...       m=matrix(N,N)
...       I = complex(0,1)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = (x0+j*delta)+ I*(y0+k*delta)
...               z=0
...               h=0
...               while (h<L and
...                      z.real**2 + z.imag**2 < R*R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m

sage: time m=mandelbrot_cy4(-2,-1.5,3,200,50)
Time: CPU 0.02 s, Wall: 0.03 s

La única parte interior a los bucles que queda por optimizar es la asignación:

m[j,k]=h

Para poder declarar arrays con tipos de datos tenemos dos opciones:

Usar punteros como en C:

...
cdef int\* m = <int\*> sage_malloc((sizeof int)\*N^2)
...

lo que conlleva peligros potenciales si calculamos mal los tamaños, y no es muy conveniente para arrays bidimensionales.

Sustituir la matriz de Sage (matrix) por un array de la librería numpy , bien integrada en cython.

Al definir el tipo de la matriz m, usamos un tipo de datos terminado en “_t”, mientras que al llamar a una de las funciones que construyen arrays (como zeros , ones o array ), pasamos el parámetro dtype, y no escribimos esa terminación. En este ejemplo usamos enteros positivos de 16 bits para los valores de m, asumiendo que no trabajaremos con un L de más de 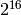$2^{16}$ .

cdef numpy.ndarray[numpy.uint16_t, ndim=2] m
m = numpy.zeros((N,N), dtype=numpy.uint16)

m[j,k]=h

sage: %cython
sage: import numpy
sage: cimport numpy   #para declarar los tipos de los arrays
...                   #tb tenemos que usar cimport
sage: def mandelbrot_cy5(float x0,float  y0,float side,
...                      int N=200, int L=50, float R=3):
...       '''returns an array NxN to be plotted with matrix_plot
...       '''
...       cdef double complex c, z, I
...       cdef float delta
...       cdef int h, j, k
...       cdef numpy.ndarray[numpy.uint16_t, ndim=2] m
...       m = numpy.zeros((N,N), dtype=numpy.uint16)
...       I = complex(0,1)
...       delta = side/N
...       for j in range(N):
...           for k in range(N):
...               c = (x0+j*delta)+ I*(y0+k*delta)
...               z=0
...               h=0
...               while (h<L and
...                      z.real**2 + z.imag**2 < R*R):
...                   z=z*z+c
...                   h+=1
...               m[j,k]=h
...       return m

sage: time m=mandelbrot_cy5(-2,-1.5,3,200,50)
Time: CPU 0.01 s, Wall: 0.01 s

No tiene sentido continuar: hemos optimizado la parte interior a los bucles, y aunque aún se puede hacer el código más rápido, el precio a pagar no nos compensa.

Más información en el manual de cython:

http://docs.cython.org/

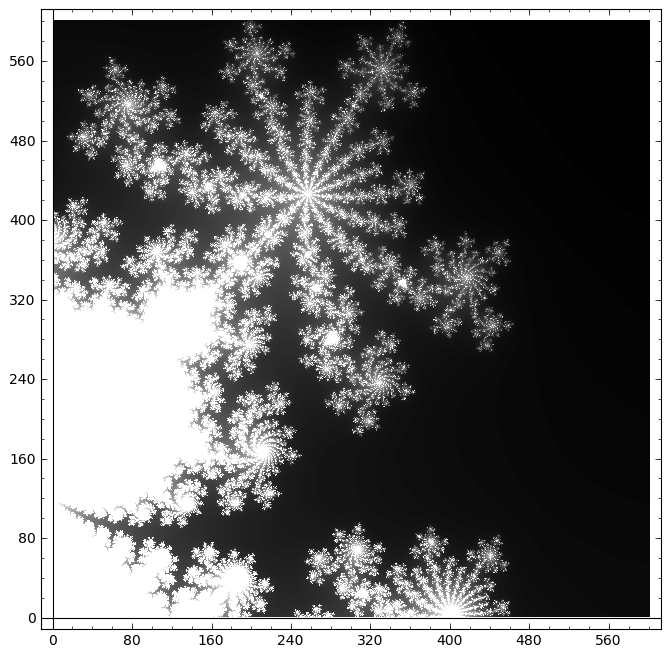
sage: time m=mandelbrot_cy5(-0.59375, 0.46875, 0.046875,600,160)
sage: matrix_plot(m).show(figsize=(8,8))
Time: CPU 0.10 s, Wall: 0.11 s

Eficiencia en cálculo científico¶

Optimiza sólo si es necesario, sólo dónde es necesario¶

Caso práctico: la constante de Brun¶

Cython¶

El conjunto de Mandelbrot¶

Optimización en cython más allá de indicar los tipos de datos (opcional)¶

Contenidos

Tema anterior

Próximo tema

Esta página

Navegación

Eficiencia en cálculo científico¶

Optimiza sólo si es necesario, sólo dónde es necesario¶

Caso práctico: la constante de Brun¶

Cython¶

El conjunto de Mandelbrot¶

Optimización en cython más allá de indicar los tipos de datos (opcional)¶

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Navegación