Ejercicios

1.

El resultado de las mediciones de %time, cputime y los demás es algo inestable. Al medir tiempos, es buena idea tomar promedios. Escribe código que almacene en una lista el tiempo promedio de ejecutar una cierta función N veces.

2.

Haz graficas que midan el tiempo de ejecución en función de su único argumento de la función es_primo definida más abajo. Asegúrate de probar la función con todos los números k en un rango [2,N]: ¿puedes explicar la forma de la gráfica?

sage: def es_primo(k):
...       return k>1 and all(k%j!=0 for j in range(2,k))

3.

Escribe código que crea una lista añadiendo elementos uno por uno, primero añadiendo los elementos al final de la lista y después añadiéndolos al final de la lista. ¿Cuaĺ debería ser la complejidad con cada enfoque?

Haz gráficas del tiempo de ejecución en función del tamaño de la lista que construyes. ¿Es consistente con la complejidad predicha?

4.

Escribe código que, partiendo de una lista de tamaño N, elimina sus elementos uno por uno hasta que la lista quede vacía. Resuelve el problema de dos formas: primero añadiendo los elementos al final de la lista y después añadiéndolos al final de la lista. ¿Cuaĺ debería ser la complejidad con cada enfoque?

Haz gráficas del tiempo de ejecución en función del tamaño de la lista. ¿Es consistente con la complejidad predicha?

5.

Compara dos formas de calcular las formas de expresar un par como suma de dos primos. La única diferencia está en el uso de una lista o de un conjunto para almacenar los números primos. Realiza gráficas de tiempo de ejecución en función de n: ¿es sensato pensar que el tiempo necesario para comprobar si un elemento pertenece a un conjunto no depende del tamaño del conjunto?

sage: def sumas1(n):
...       if n%2!=0:
...           #Si n es impar, no devolvemos nada
...           return
...       else:
...           lista = []
...           primos = prime_range(n)
...           for k in primos:
...               if n-k in primos:
...                   lista.append((k,n-k))
...           return lista

sage: def sumas2(n):
...       if n%2!=0:
...           #Si n es impar, no devolvemos nada
...           return
...       else:
...           lista = []
...           primos = set(prime_range(n))
...           for k in primos:
...               if n-k in primos:
...                   lista.append((k,n-k))
...           return lista

6.

Encuentra todos los números primos menores que un millón que son de la forma 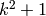, con 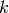un número triangular.

7.

Encuentra el menor número primo con k dígitos decimales distintos, para k=5,6,7. Resuelve el problema de las dos formas siguientes:

• Crea una lista de primos candidatos con prime_range, y busca entre ellos el primero con la propiedad pedida. Este enfoque obliga a fijar una cota máxima y buscar primos menores que esa cota.
• Genera los números primos de uno en uno usando next_prime. En este enfoque no hay que fijar una cota a priori.

8.

Observa que ningún primo menor que 10000 puede tener menos de 5 cifras. Podemos por tanto comenzar la búsqueda por este número. Apurando un poco más, podemos comenzar a buscar primos por el menor número con cinco cifras distintas, el 10234. Incorpora esta información y mide la mejora en tiempo de ejecución.