Elementos finitos

Acabamos de discutir, en la sección anterior, el fracaso de este enfoque. Este hecho, que hemos constatado de manera independiente, parece ser conocido en la comunidad de optimización geométrica, donde se define el operador de Laplace-Beltrami sobre superficies[27].

Para completar la discusión, señalamos que es también posible formular expresiones para la divergencia y el gradiente mediante el método de elementos finitos. Es fácil ver que la matriz de masas es la misma, pero que en vez de la matriz de rigidez hay que considerar la matriz de vectores con componentes

$$\mathbf{G}_{ab}=\int s_a \nabla s_b .$$

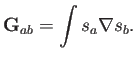
De este modo se pueden obtener aproximaciones para la divergencia y el gradiente que, curiosamente, convergen para disposiciones sobre mallas regulares (su error $L_2$ , como $N^{-1}$ ) y también para posiciones aleatorias (como $N^{-1/2}$ ). Sin embargo, la combinación de ambas para formar el laplaciano sigue sin converger para disposiciones aleatorias (para regulares sí lo hace, como $N^{-1/4}$ ).