Fuerzas viscosas

Si, por el contrario, existen fuerzas viscosas, estas contribuirán al tensor de esfuerzos. El caso más sencillo es el de los fluidos newtonianos, para los cuales el tensor de esfuerzos es proporcional al de deformaciones.

Expresando esta linealidad, y teniendo en cuenta la isotropía de los fluidos, se puede escribir en la base que diagonaliza los dos tensores (la diagonalización es simultánea al ser ambos proporcionales):

$$\tau_1=-p+K\epsilon_1 + \lambda (\epsilon_1+\epsilon_2+\epsilon_3),$$

siendo ésta la expresión más genérica permitida. Al rotar los ejes para pasar a otro sistema de referencia, la conclusión es:

$$\tau_{ii}=-p+K\epsilon_{ii}+ \lambda \nabla\cdot v,$$

y para los elementos de fuera de la diagonal, con $j\ne i$ :

$$\tau_{ik}= K\epsilon_{ij} .$$

Una aplicación de estas ecuaciones a un fluido newtoniano entre dos placas planas paralelas revela que el esfuerzo en el fluido es

$$\tau_{xy}= \frac{K}{2} \frac{V}{h} ,$$

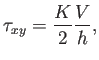
donde $V$ es la velocidad relativa de las placas y $h$ su separación. Históricamente, esta relación se utiliza para definir (y medir) el coeficiente de viscosidad (dinámica) $\mu$ :

$$\tau_{xy}=\mu \frac{V}{h} ,$$

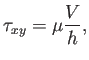
así pues $K=2\mu$ .

En cuanto a $\lambda$ , esta cantidad sería un segundo coeficiente de viscosidad, denominado coeficiente de Lamé en elasticidad. Fijémonos que la traza del tensor de esfuerzos satisfará

$$-\frac{\mathrm{Tr}}{3}= p-(\lambda+\frac{2}{3}\mu)\nabla\cdot v.$$

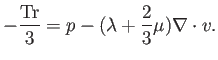
El papel de la ``presión extra'' $-(\lambda+2\mu/3)\nabla\cdot v$ suele por lo general ignorarse, alegando una de estas dos condiciones:

• La combinación $\lambda+2\mu/3$ es nula. Esto define un fluido ``stokesiano''.
• El flujo es prácticamente incompresible, así que $\nabla\cdot v$ es despreciable.

La primera condición, totalmente ad hoc parece no sostenerse en la práctica; de hecho, $\lambda$ parece ser positivo en las (escasas) medidas que se han realizado, así que a duras penas puede satisfacerse. La segunda, en cambio, sí puede sostenerse en muchas ocasiones. Al final, sólo hay algunos problemas de interés en los cuales el término no puede (o debe) ignorarse, como ondas de choque o atenuación de ondas de sonido.