Varias dimensiones

En la discusión anterior, se han desarrollado expresiones que valen sólo para una dimensión espacial. En varias dimensiones, las expresiones son muy similares. La energía es:

$$E=\beta_{ij} \left[\sum_a s_{a i}(x_i- x_{a i})(x_j- x_{a j}) \right] ,$$

es decir, $\beta$ es ahora un tensor de dimensión $2$ y tamaño $d \times d$ . Los subíndices $a$ y $b$ se reservan para enumerar los nodos, y los $i$ , $j$ ...para las coordenadas cartesianas. Se supone la regla de suma de Einstein para estas últimas: cuando hay índices repetidos se debe sumar para todas las dimensiones espaciales. Como es obvio, el tensor debe ser simétrico, ya que $x_i x_j=x_j x_i$ .

El término de ligadura para la consistencia de primer orden pasa a ser

$$L_1=\lambda_i \left(\sum_a s_{a i} (x_{a i} - x_i) \right) ,$$

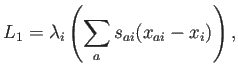
así que $\lambda$ es ahora un vector de longitud $d$ .

Al extremizar la función, la solución tiene la misma forma, ecuación (6.1), pero el exponente es:

$$f_a=\lambda_i (x_i - x_{ai}) - \beta_{ij} (x_i - x_{ai})(x_j - x_{aj}).$$ (6.5)

Por supuesto, la minimización no es ahora con respecto a un sólo parámetro, sino con respecto a cada una de las componentes de $\lambda$ : $d$ componentes independientes en $d$ dimensiones.