Triangulaciones

Sin entrar en muchos detalles matemáticos, la idea intuitiva de una triangulación es que indica la figura 3.1: una colección de triángulos que no se intersecan, cuyos vértices son los nodos^3.1. La triangulación llena el espacio dentro de la envolvente conexa del conjunto de nodos. Todos los nodos están rodeados por triángulos, salvo los los que queden más ``expuestos'', que forman parte justamente de la envolvente conexa. Para tratar estos nodos igual que los otros se puede introducir un vértice infinito, que está conectado a éstos y situado en el infinito (una idea similar a la de Riemann, que asigna el polo norte de una esfera al punto del infinito del plano proyectivo). Este es el método implementado en CGAL. La triangulación define además una relación de vecindad entre nodos que estén conectados por un lado de un triángulo.

Figura: Ejemplo de una triangulación. La envolvente convexa es el polígono azul. Los nodos pertenecientes a ella se consideran veciones del vértice infinito en ciertas implementaciones.

De todas las posibles triangulaciones (cuyo número puede ser enorme, ya que crece como 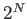$2^N$ ), existe una única (salvo casos degenerados, como se discutirá) llamada de Delaunay, introducida por Delone en 1924^3.2. Una de sus posibles definiciones es la siguiente propiedad:

Propiedad 1   Círculos vacíos: La triangulación de Delaunay verifica que las circunferencias circunscritas de uno de los triángulos no contienen ningún nodo en su interior.

La figura 3.2 muestra dos posibilidades de triangulación de cuatro nodos. De las dos posibles, la dibujada en azul es la de Delaunay, al cumplir la condición.

Figura 3.2: Dos posibles triangulaciones de cuatro nodos. La azul es la de Delaunay (el círculo circunscrito no engloba al cuarto nodo), la roja no lo es.

Esta condición indica claramente qué casos pueden ser problemáticos: en configuraciones llamadas ``degeneradas'' puede que haya dos posibilidades de triangulación; en este caso, habrá un nodo sobre circunferencia circuscrita. Este caso se muestra en la figura 3.3.

Figura 3.3: Caso degenerado: tanto la conexión roja como la azul corresponden a triangulaciones de Delaunay.

Otra propiedad muy importante de estas triangulaciones queda patente en la figura 3.2:

Propiedad 2   Triángulos más equiláteros: la triangulación de Delaunay es la que produce los ángulos internos más abiertos.

Es decir, los triángulos resultantes son siempre ``más equilateros'' que los de otras triangulaciones. Esto puede demostrarse rigurosamente y tiene importantes consecuencias en el método de elementos finitos, como se discutirá más adelante, en el cual los triángulos ``poco equiláteros'' no son deseables.

Existen otras propiedades importantes, por ejemplo:

Propiedad 3   Distancia mínima: los vértices más próximos entre sí están necesariamente unidos por la triangulación de Delaunay.