Conservación de la masa

La manera más elegante de obtener las ecuaciones de movimiento es a partir de ecuaciones de conservación. Para empezar, supongamos que una partícula tiene masa $m$ . Desde el punto de vista lagrangiano, la conservación de la masa es simplemente

$$m = m_0 ,$$ (2.2)

donde $m_0$ es la masa inicial. Si el volumen de la partícula es $\mathcal{V}$ y su densidad, por tanto $\rho=m/\mathcal{V}$ , la expresión anterior significa

$$\rho\mathcal{V}= \rho_0\mathcal{V}_0 ,$$

donde $\rho_0$ es la distribución inicial de densidad. (ver [3], p. y [4] p. 61). Matemáticamente, esta expresión puede entenderse como un cambio de variables que sólo sería válido dentro de una integración; el jacobiano del cambio de $\mathcal{V}_0$ a $\mathcal{V}$ sería $\rho/\rho_0$ .

Desde el punto de vista euleriano, en cambio, la conservación se escribiría

$$\frac{d m}{d t}= 0 .$$

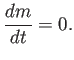
Poniendo $m=\rho\mathcal{V}$ ,

$$\mathcal{V}\frac{d \rho}{d t} + \rho \frac{\mathcal{V}}{dt} = 0 .$$

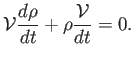
Como vimos en la sección anterior, el cambio relativo de $\mathcal{V}$ es la parte de dilatación (la diagonal) del tensor de deformaciones, que a su vez es la divergencia de la velocidad:

$$\frac{1}{\mathcal{V}}\frac{\mathcal{V}}{dt} = \nabla\cdot v .$$ (2.3)

Es decir,

$$\frac{d \rho}{d t} = - \rho \nabla v ,$$ (2.4)

una expresión que Monaghan denomina, jocosamente, ``de la convergencia'', ya que $-\nabla v$ sería ``la convergencia'' de $v$ [5].

Esta expresión, recordando que la derivada temporal es la derivada material, puede escribirse también

$$\frac{\partial \rho}{\partial t} + \nabla \rho v =0 ,$$ (2.5)

ecuación que se conoce como ``de continuidad''.

Una maneral más habitual de llegar a esta ley es la siguiente: si la masa en una regíon del espacio es $\int_V \rho$ , su cambio vendrá dado por el flujo de materia a través de la superficie que rodea esta masa, $- \int_S (\rho v) \cdot n$ (el signo menos se introduce porque el vector normal a la superficie, $n$ , apunta por convención hacia afuera, así que un integrando positivo representa una pérdida). Introduciendo la derivada temporal en la integral y aplicando el teorema de la divergencia de Gauss se llega a la misma conclusión.