Puntos de vista de Euler y de Lagrange

A la hora de expresar las distintas ecuaciones, se ha venido distinguiendo dos puntos de vista complementarios. El primero, llamado ``lagrangiano''^2.1 es el más similar a un enfoque mecánico habitual: el énfasis se pone en la trayectoria de las partículas del fluido.

Estas partículas se entienden hoy como se entendían hace 200 años: desde el punto de vista matemático son puntos, pero se entiende que desde el punto de vista físico son porciones materiales dotadas de magnitudes macroscópicas. Hoy sabemos que la materia es discreta, pero el tamaño atómico y molecular es tan pequeño que esta definición sigue siendo válida en casi todos los casos.

La trayectoria de estas partículas estará descrita por un vector de posición $r$ que cambia con el tiempo. Si la partícula estaba en el punto $r_0$ en el instante inicial, la colección de todas las trayectorias del fluido con el tiempo es

$$r=r(r_0,t) ,$$

lo que matemáticamente sería un mapeo del espacio $r_0\rightarrow r$ con un parámetro $t$ .

Por definición, las partículas siguen una velocidad, que es un campo que satisfará

$$v=\frac{\partial r}{\partial t} .$$ (2.1)

En la Ref. [3], p. xxx incluso se escribe $(\partial r/\partial t)_{r_0}$ para enfatizar que se trata de una derivada sólo temporal.

En el punto de vista ``euleriano'', en cambio, se supone un marco fijo de referencia sobre el cual cambian los campos hidrodinámicos. La trayectoria de las partículas pasa a jugar un papel menor y el campo principal es más bien el de velocidades. Esto es también natural para un fluido, ya que las partículas en muchos casos siguen trayectorias que vienen de lejos, y van a sitios también lejanos, mientras que su velocidad en cada punto puede ser más constante (como ilustra la cita de Heráclito al comienzo de este capítulo).

En este sentido, la variación temporal de cualquier magnitud física referente al fluido, $A$ , no vendrá dada simplemente por su derivada con respecto a su dependencia explícita del tiempo. Como también la posición de la partícula puede variar con el tiempo, la variación vendrá dada por la regla de la cadena:

$$\frac{d A}{d t} = \frac{\partial A}{\partial t} + \frac{\partial ... ...y}{\partial t} + \frac{\partial A}{\partial z} \frac{\partial z}{\partial t} .$$

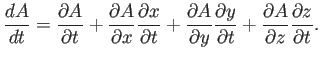
Como se ha discutido, la derivada de la posición de la partícula con respecto al tiempo es la velocidad, así que podemos escribir

$$\frac{d A}{d t} = \frac{\partial A}{\partial t} + (v \cdot \nabla) A ,$$

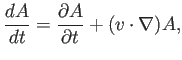
donde hay que entender el operador $v \cdot \nabla$ como

$$v \cdot \nabla= \frac{\partial x}{\partial t} \frac{\partial }{\p... ...l }{\partial y} + \frac{\partial z}{\partial t} \frac{\partial }{\partial z} .$$

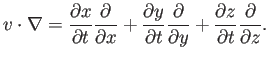
Esta derivada se denomina justamente derivada particular (``de las partículas''), o material^2.2.