Malabares, matemáticas, Sage
 |
 |
Grafos con Sage para resolver un problema lúdico
En esta charla vamos a usar:
- Algunas nociones básicas de "Teoría de Grafos"

- ...y...
...un malabarista.

...suelo trabajar con Daniel Sánchez, ¡¡pero no hemos podido traerle!!
Solución: un malabarista virtual
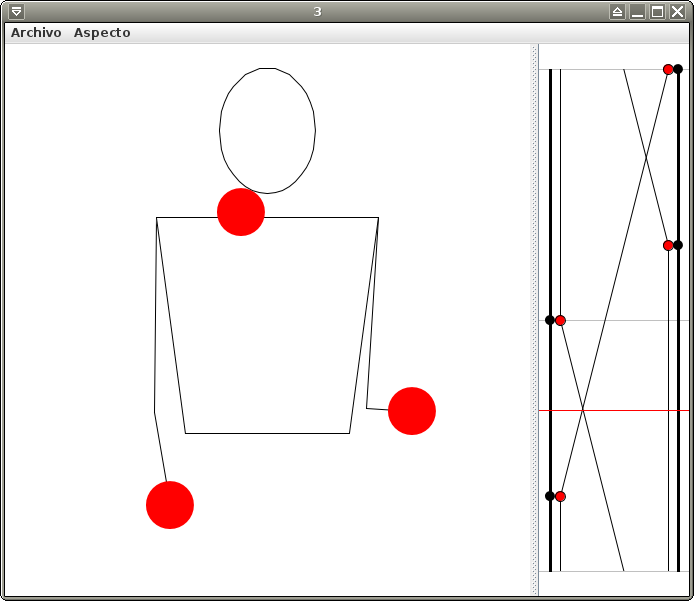
...vamos a usar Jugglinglab, pero hay muchos otros.
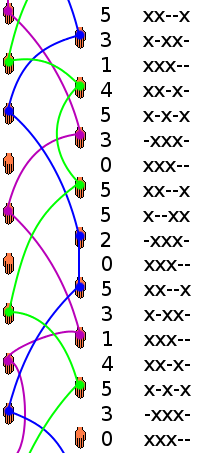
Siteswap
|
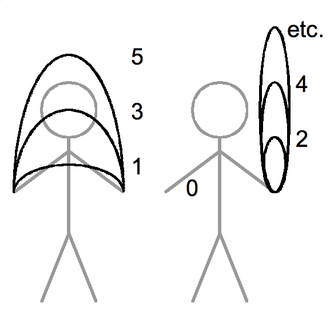 Si el malabarista tiene dos manos, usa la mano izquierda en los pulsos impares, y la derecha en los pulsos pares.
Si el malabarista tiene dos manos, usa la mano izquierda en los pulsos impares, y la derecha en los pulsos pares.
|
Siteswap
|
 |
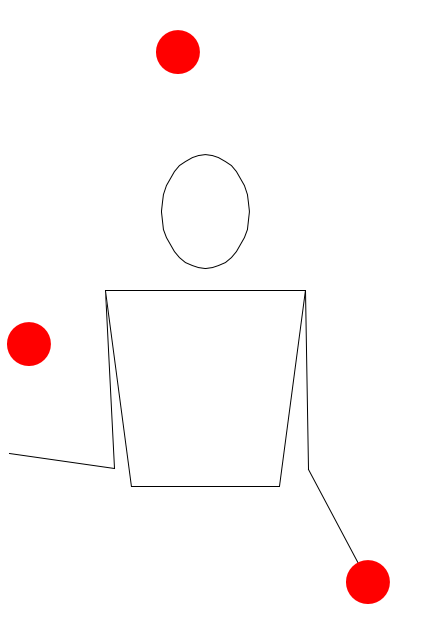
...vamos a verlo con Juggling Lab
¿Podéis decirme qué trucos hace el malabarista virtual?
SageMath
Es fácil comprobar si una secuencia finita es un patrón de siteswap periódico.
def validate(lanza):
N = len(lanza)
recoge = [0]*len(lanza)
for j,k in enumerate(lanza):
if recoge[(j+k)%N]>0:
return False
recoge[(j+k)%N] = 1
return True
def validate_bis(seq):
return len(set((j+k)%N for j,k in enumerate(seq) )) == len(seq)
Pero: ¿podemos listar todos los patrones de siteswap posibles?
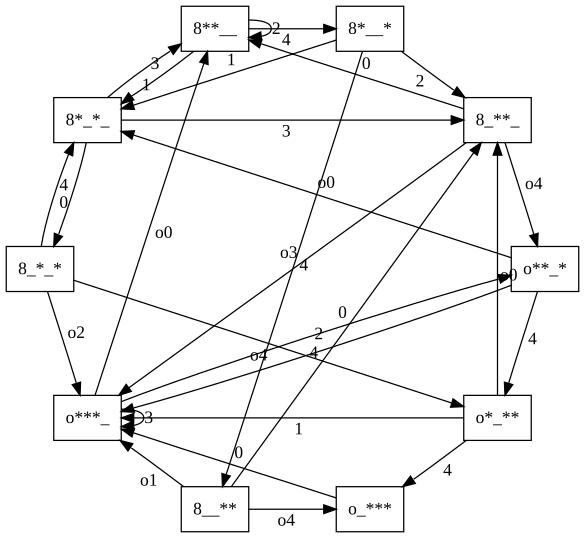
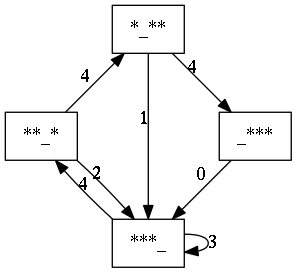
Estados
- Un instante está caracterizado por los tiempos esperados de caída de cada bola.
- Un estado sólo es válido si cada bola en el aire caerá en un instante futuro distinto.
- Por tanto, podemos representar un estado mediante una secuencia de bola '*' y no bola '_': en la posición i-ésima ponemos una bola si se espera que una bola caiga dentro de i instantes y no-bola si ninguna bola caerá dentro de i instantes.
- Por ejemplo '**__*' quiere decir que hay tres bolas en el aire y que caerán dentro de 1, 2 y 5 instantes.
Diagrama de estados
|
 |
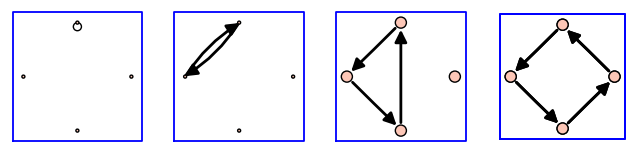
Grafos en Sage
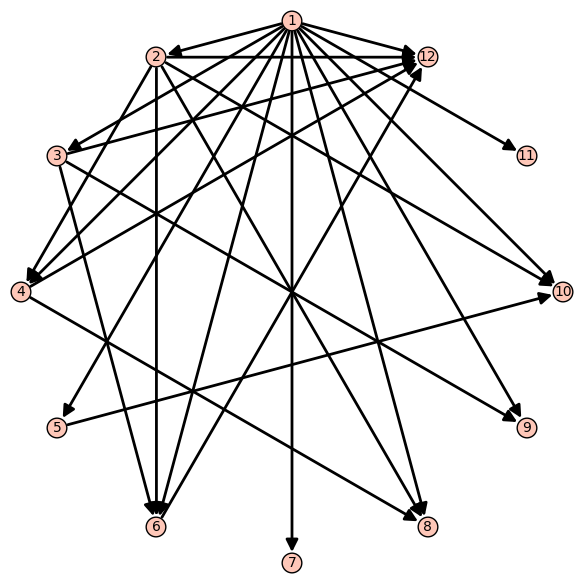
Definir grafos
g = DiGraph()
N = 12
for k in [1..N]:
for j in k.divisors():
g.add_edge(j,k)
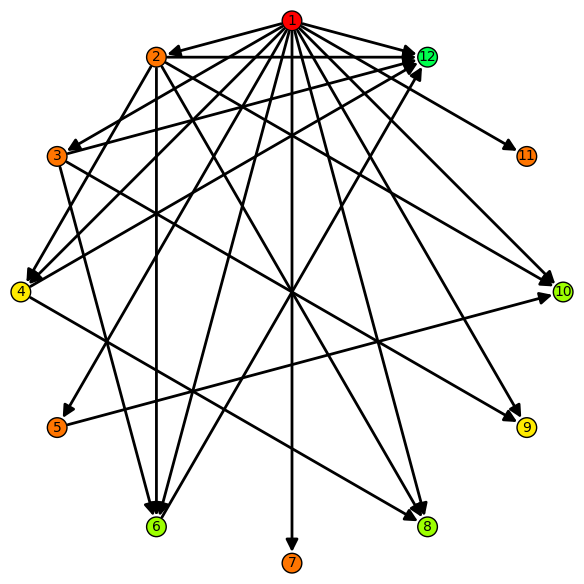
¿Qué grafo es éste?
Dibujar grafos
g.plot(layout='circular')
Hay muchas opciones para dibujar grafos
g.plot(layout='circular',
partition=[[v for v in g if g.in_degree(v)==k]
for k in [0..N]])
Pasamos a Sage

pincha en la imagen para ver la hoja interactiva en la wiki de Sage de la Universidad de Zaragoza.
Extras
Para profundizar
pincha en las imágenes para ver las hojas interactivas en la wiki de Sage de la Universidad de Zaragoza.

Introducción a grafos en Sage
Notas sacadas de la asignatura: Laboratorio de Matemáticas
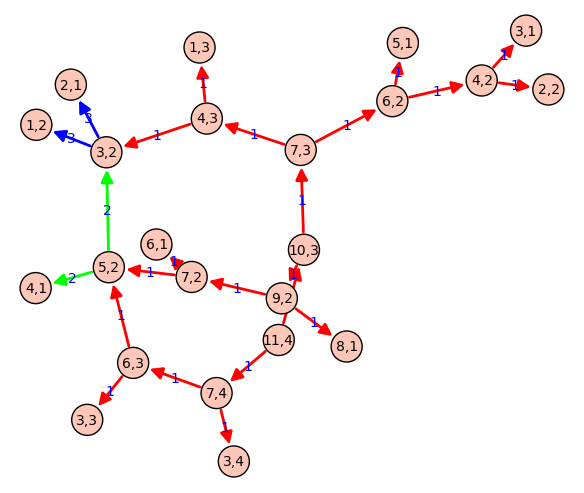
Grafo de llamadas de una función recursiva
Teorema de Wagner
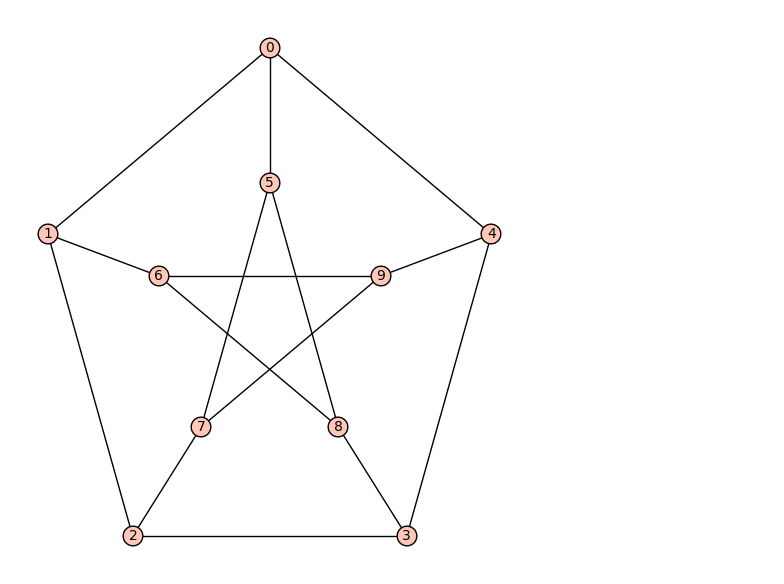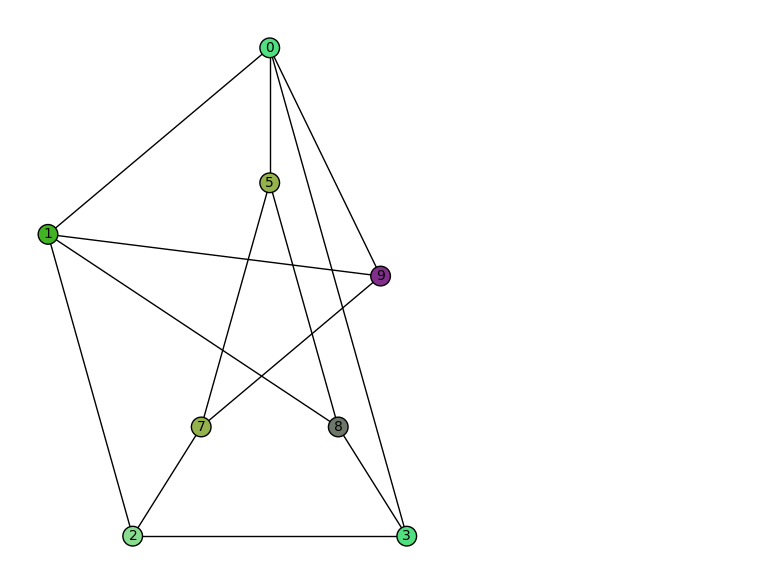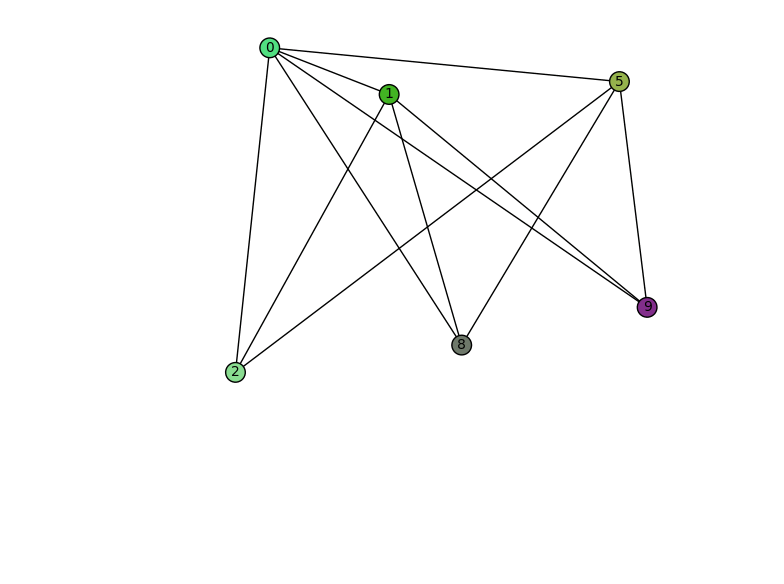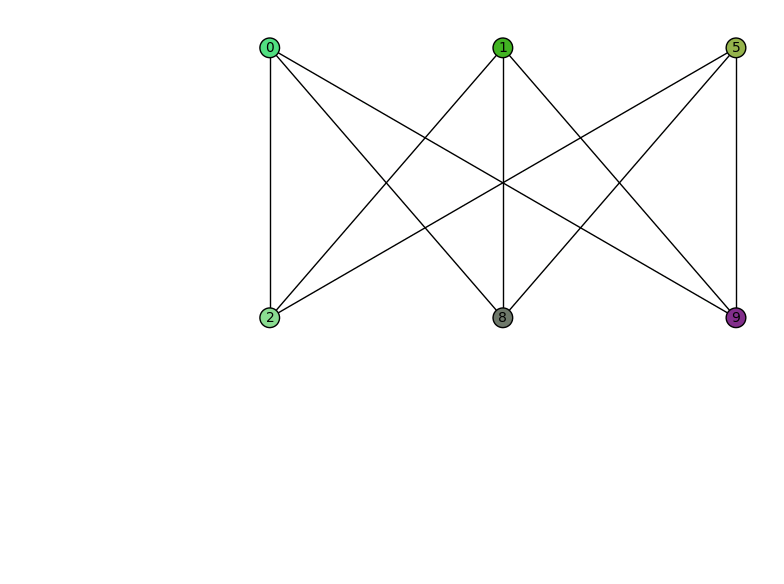
Animaciones con grafos
Cadenas de Markov absorbentes
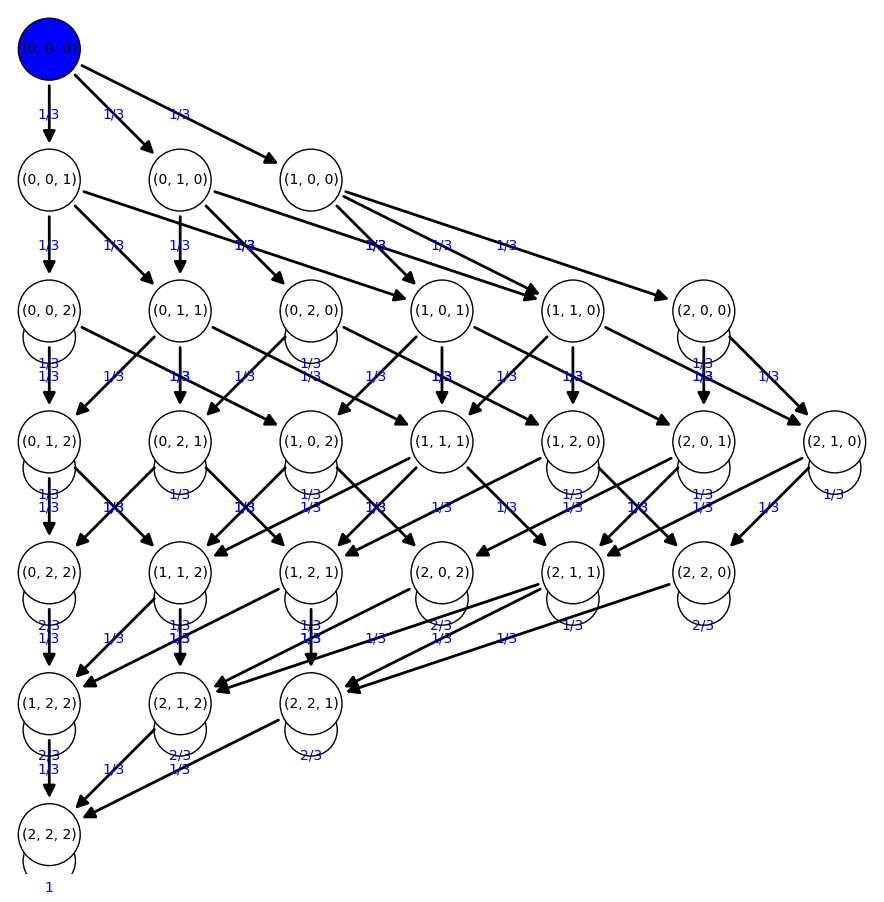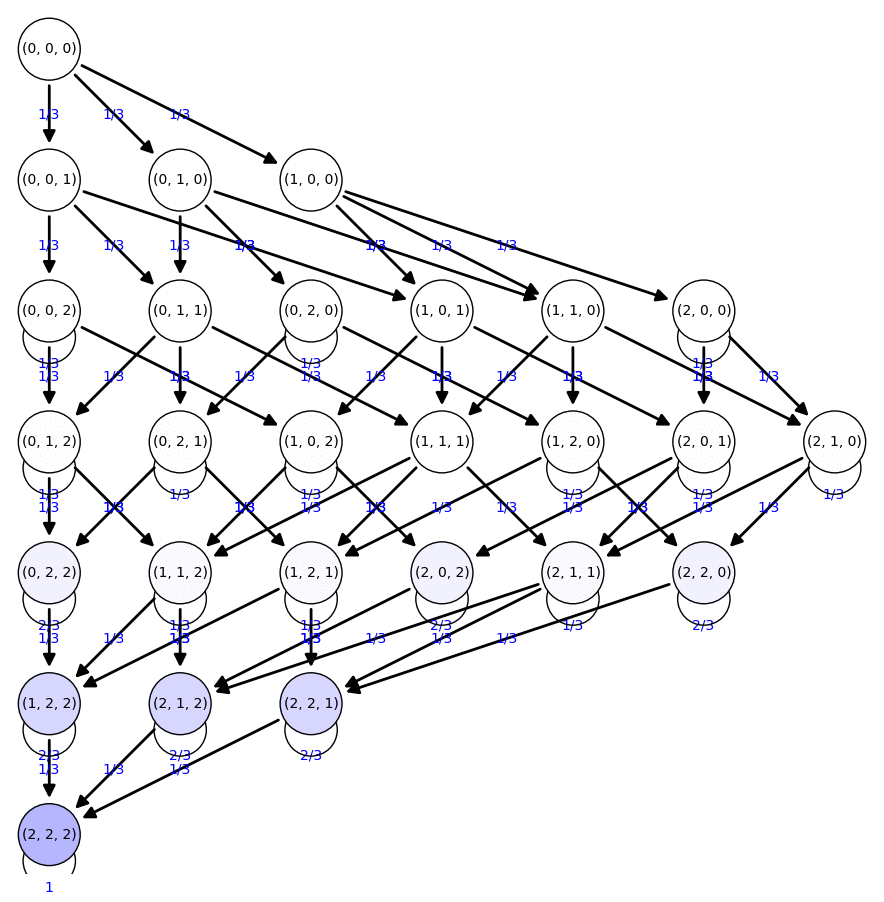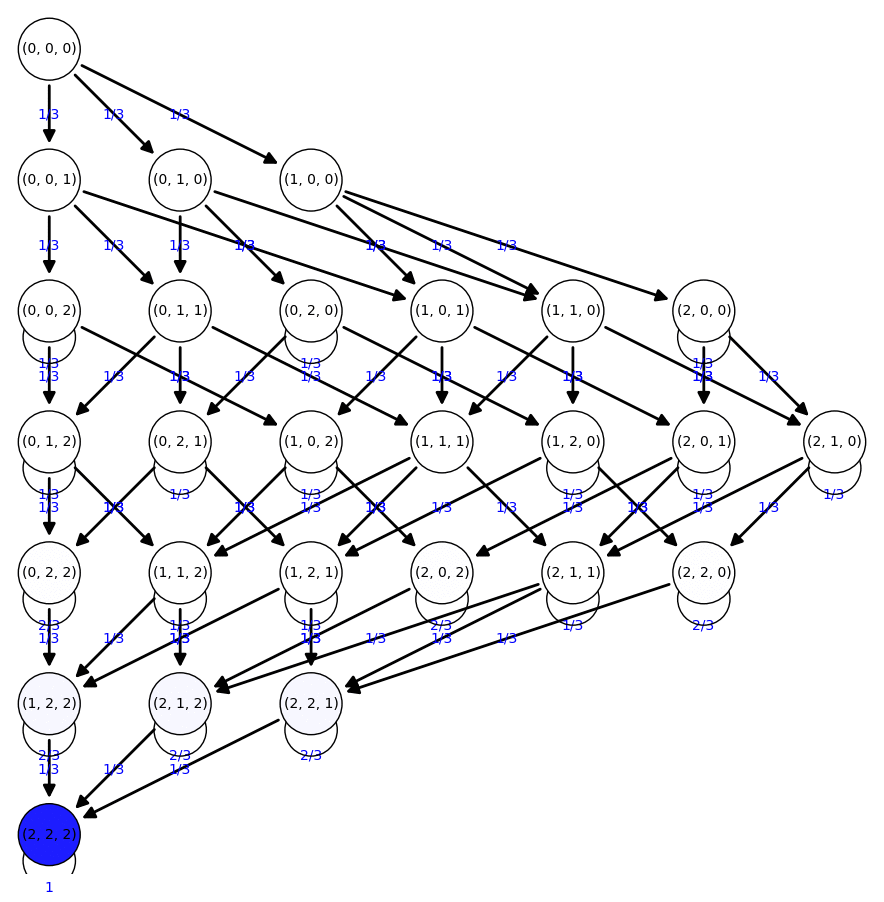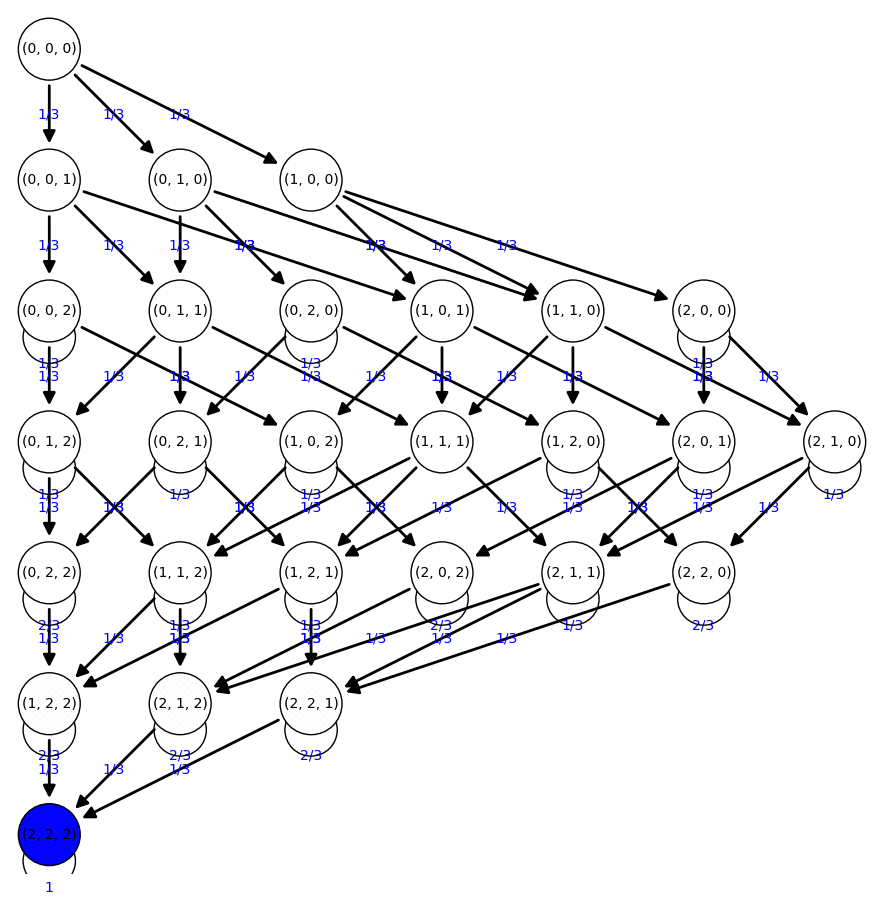
Agradecimientos

- Daniel Sánchez (Fausto)
- Wikipedia
- Juggling Lab