Combinatoria, Probabilidad y Estadística con Sage¶

Breve resumen de las capacidades de Sage¶

Combinatoria: Sage está muy avanzado, gracias sobre todo a sage-combinat, matemáticos principalmente franceses. Historia: Mupad-combinat se va a pique cuando otra compañía compra Mupad.
Grafos: Muy completo, muy fácil de usar. Contiene la librería de grafos networkx, específica para python, muy bien integrada, y tiene implementaciones de otros muchos algoritmos.
Probabilidad: Para enseñar probabilidad y estadística elementales, Sage puede ser suficiente para dar clase. Herramientas de cálculo simbólico para trabajar con distribuciones de probabilidad, variedad de gráficas para representar, python es buen lenguaje para escribir simulaciones.
Estadística: Para una asignatura de estadística, R es probablemente mejor opción...

R y Sage¶

Sage incluye R, pero la integración no es buena.

Podemos usar el servidor de Sage para usar R desde el navegador:

Puedes seleccionar “r” en el desplegable de lenguaje en una hoja de trabajo de Sage (a la derecha del menú “data”), y entonces todos los recuadros de código se interpretarán como código de R.

Puedes comenzar cada bloque de código con %r.

%r
datos <- c(2,1,2,2,3,2,1);
summary(datos)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  1.000   1.500   2.000   1.857   2.000   3.000

.

Pero en una instalación ‘normal’, no podemos ver gráficas en el ordenador. El siguiente error es típico:

%r
hist(datos);
Error in png() : X11 is not available

...hay una solución en ask.sagemath.org.

Pero deberías probar el servidor de RStudio, un interfaz para R de software libre.

Un primer ejemplo: lanzamientos de monedas¶

Lanzamos 10 monedas de una en una sobre la mesa: ¿cuál es la probabilidad de que nunca haya más cruces que caras sobre la mesa?

Dos enfoques típicos de quien tiene un ordenador:

Contar los casos favorables y dividir ese número por el caso de casos posibles.

Simular el experimento usando los números aleatorios del ordenador una cantidad lo bastante grande de veces, y apelar a la ley de los grandes números.

Codificamos:

Cruz: 0. Cara: 1

Una secuencia de 10 lanzamientos: una lista de 1’s y 0’s.

Comenzamos por escribir una función que identifica un caso favorable, que usaremos en ambos enfoques:

sage: def es_favorable(ms):
...       #ms es una lista de 0's y 1's
...       caras = 0
...       for j,m in enumerate(ms):
...           if m:
...               caras += 1
...           cruces = j+1-caras
...           #si en algun momento hay mas cruces que caras, no es favorable
...           if caras < cruces:
...               return False
...       return True
sage: print es_favorable([1,0,0,1])
False
sage: print es_favorable([1,0,1,0])
True

Primer enfoque: tenemos que recorrer todas las listas con 0 y 1 en cada posición.

Anidar 10 bucles no es sensato:

for k1 in [0,1]:
    for k2 in [0,1]:
        for k3 in [0,1]:
            for k4 in [0,1]:
                for k5 in [0,1]:
...

‘Truco’: cuando un entero k recorre los números desde 0 hasta 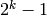$2^k -1$ , sus bits recorren todas las posibles combinaciones de 0 y 1 para K variables.

Podemos usar, el método digits() pasando los argumentos base=2 y padto=K (devuelve siempre listas de longitud K).

Este método lo tienen todos los enteros de SAGE (cuidado: usa srange, no range).

sage: K=4
sage: for k in srange(2^K):
...       vars = k.digits(base=2,padto=K)
...       print vars
[0, 0, 0, 0]
[1, 0, 0, 0]
[0, 1, 0, 0]
[1, 1, 0, 0]
[0, 0, 1, 0]
[1, 0, 1, 0]
[0, 1, 1, 0]
[1, 1, 1, 0]
[0, 0, 0, 1]
[1, 0, 0, 1]
[0, 1, 0, 1]
[1, 1, 0, 1]
[0, 0, 1, 1]
[1, 0, 1, 1]
[0, 1, 1, 1]
[1, 1, 1, 1]

y ya podemos aplicar el primer enfoque:

sage: K = 10
sage: totales    = 2^K
sage: favorables = 0
sage: for k in srange(totales):
...       vars = k.digits(base=2,padto=K)
...       if es_favorable(vars):
...           favorables += 1
sage: p = favorables/totales
sage: print '%s=%.3f'%(p,p)
63/256=0.246

.

Para el segundo enfoque, necesitamos listas con 0’s y 1’s elegidos aleatoriamente...
...y el resto es igual.

sage: K = 10
sage: totales = 1000
sage: favorables = 0
sage: for _ in srange(totales):
...       vars = [randint(0,1) for _ in srange(K)]
...       if es_favorable(vars):
...           favorables += 1
sage: p = favorables/totales
sage: print '%s=%.3f'%(p,p)
27/100=0.270

Objetos combinatorios¶

Muchos objetos combinatorios ya están definidos en Sage.

Tienen una estructura uniforme, con métodos comunes y una jerarquía de clases.

Métodos perezosos (no se hace ningún cálculo hasta que es imprescindible)

Podemos trabajar con objetos muy grandes, incluso infinitos.

Un método para construir todos los elementos y otro para contarlos.

Métodos interesantes:

cardinality() para obtener el número de elementos

list() para obtener la lista de todos los elementos

random_element() para obtener un elemento aleatorio

Iteraciones del tipo for objeto in Clase para recorrer los objetos sin necesidad de cargarlos todos en memoria.

Objetos interesantes:

Subsets: Subsets(lista) recorre los subconjuntos de lista (puede ser cualquier iterable). Admite un segundo argumento Subsets(lista, tamanyo) para recorrer únicamente los subconjuntos del tamaño especificado.

Permutaciones: Permutations(lista) recorre las ordenaciones de lista.

Particiones: Partitions(k) recorre las formas de sumar k con enteros positivos. Además admite argumentos extra para limitar más las particiones.

Vectores de enteros: IntegerVectors recorre las formas de sumar un entero con enteros no negativos. También admite argumentos extra.

WeightedIntegerVectors recorre las formas de sumar un entero usando los enteros de una lista dada (¿de cuántas formas puedo pagar 33 euros usando billetes de 5 y monedas de 2?)

CartesianProduct producto cartesiano de dos conjuntos.

Nota: recuerda que la ayuda del objeto se obtiene escribiendo una interrogación después de su nombre: Partitions?

Ejemplos¶

sage: #Una permutacion aleatoria de una lista
sage: print Permutations(srange(4)).random_element()
[2, 3, 1, 0]

sage: #Todas las formas de sumar 5 con números positivos
sage: print Partitions(5).list()
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1], [1, 1, 1, 1, 1]]

sage: #Todas las formas de sumar 8 usando monedas de 1, 2 y 5
sage: print WeightedIntegerVectors(8, [1,2,5]).list()
[[1, 1, 1], [3, 0, 1], [0, 4, 0], [2, 3, 0], [4, 2, 0], [6, 1, 0], [8, 0, 0]]

sage: #Por si acaso no te creias que para calcular el cardinal no hace falta
sage: #calcular todos los elementos
sage: S = Set([1,2,3,4])
sage: S3 = Subsets(Subsets(Subsets(S)))
sage: print S3.cardinality()
2003529930406846464979072351560255750447825475569751419265016973710894059556311453089506130880933348101038234342907263181822949382118812668869506364761547029165041871916351587966347219442930927982084309104855990570159318959639524863372367203002916969592156108764948889254090805911457037675208500206671563702366126359747144807111774815880914135742720967190151836282560618091458852699826141425030123391108273603843767876449043205960379124490905707560314035076162562476031863793126484703743782954975613770981604614413308692118102485959152380195331030292162800160568670105651646750568038741529463842244845292537361442533614373729088303794601274724958414864915930647252015155693922628180691650796381064132275307267143998158508811292628901134237782705567421080070065283963322155077831214288551675554073345107213112427399562982719769150054883905223804357045848197956393157853510018992000024141963706813559840464039472194016069517690156119726982337890017641517190051133466306898140219383481435426387306539552969691388024158161859561100640362119796101859534802787167200122604642492385111393400464351623867567078745259464670903886547743483217897012764455529409092021959585751622973333576159552394885297579954028471943529913543763705986928913757153740001986394332464890052543106629669165243419174691389632476560289415199775477703138064781342309596190960654591300890188887588084733625956065444888501447335706058817090162108499714529568344061979690565469813631162053579369791403236328496233046421066136200220175787851857409162050489711781820400187282939943446186224328009837323764931814789848119452713007440220765680910376203999203492023906626264491909167985461515778839060397720759279378852241294301017458086862263369284725851403039615558564330385450688652213114813638408384778263790459607186876728509763471271988890680478243230394718650525660978150729861141430305816927924971409161059417185352275887504477592218301158780701975535722241400019548102005661773589781499532325208589753463547007786690406429016763808161740550405117670093673202804549339027992491867306539931640720492238474815280619166900933805732120816350707634351669869625020969023162859350071874190579161241536897514808261904847946571736601005892476655445840838334790544144817684255327207315586349347605137419779525190365032198020108764738368682531025183377533908861426184800374008082238104076468878471647552945326947661700424461063311238021134588694532200116564076327023074292426051582811070387018345324567635625951430032037432740780879056283663406965030844225855967039271869461158513793386475699748568670079823960604393478850861649260304945061743412365828352144806726676841807083754862211408236579802961200027441324438432402331257403545019352428776430880232850855886089962774458164680857875115807014743763867976955049991643998284357290415378143438847303484261903388841494031366139854257635577105335580206622185577060082551288893332226436281984838613239570676191409638533832374343758830859233722284644287996245605476932428998432652677378373173288063210753211238680604674708428051166488709084770291208161104912555598322366244868556651402684641209694982590565519216188104341226838996283071654868525536914850299539675503954938371853405900096187489473992880432496373165753803673586710175783994818471798498246948060532081996066183434012476096639519778021441199752546704080608499344178256285092726523709898651539462193004607364507926212975917698293892367015170992091531567814439791248475706237804600009918293321306880570046591458387208088016887445835557926258465124763087148566313528934166117490617526671492672176128330845273936469244582892571388877839056300482483799839692029222215486145902373478222682521639957440801727144146179559226175083889020074169926238300282286249284182671243405751424188569994272331606998712986882771820617214453142574944015066139463169197629181506579745526236191224848063890033669074365989226349564114665503062965960199720636202603521917776740668777463549375318899587866282125469797102065747232721372918144666659421872003474508942830911535189271114287108376159222380276605327823351661555149369375778466670145717971901227117812780450240026384758788339396817962950690798817121690686929538248529830023476068454114178139110648560236549754227497231007615131870024053910510913817843721791422528587432098524957878034683703337818421444017138688124249984418618129271198533315382567321870421530631197748535214670955334626336610864667332292409879849256691109516143618601548909740241913509623043612196128165950518666022030715613684732364660868905014263913906515063908199378852318365059897299125404479443425166774299659811849233151555272883274028352688442408752811283289980625912673699546247341543333500147231430612750390307397135252069338173843322950701049061867539433130784798015655130384758155685236218010419650255596181934986315913233036096461905990236112681196023441843363334594927631946101716652913823717182394299216272538461776065694542297877071383198817036964588689811863210976900355735884624464835706291453052757101278872027965364479724025405448132748391794128826423835171949197209797145936887537198729130831738033911016128547415377377715951728084111627597186384924222802373441925469991983672192131287035585307966942713416391033882754318613643490100943197409047331014476299861725424423355612237435715825933382804986243892498222780715951762757847109475119033482241412025182688713728193104253478196128440176479531505057110722974314569915223451643121848657575786528197564843508958384722923534559464521215831657751471298708225909292655638836651120681943836904116252668710044560243704200663709001941185557160472044643696932850060046928140507119069261393993902735534545567470314903886022024639948260501762431969305640666366626090207048887438898907498152865444381862917382901051820869936382661868303915273264581286782806601337500096593364625146091723180312930347877421234679118454791311109897794648216922505629399956793483801699157439700537542134485874586856047286751065423341893839099110586465595113646061055156838541217459801807133163612573079611168343863767667307354583494789788316330129240800836356825939157113130978030516441716682518346573675934198084958947940983292500086389778563494693212473426103062713745077286156922596628573857905533240641849018451328284632709269753830867308409142247659474439973348130810986399417379789657010687026734161967196591599588537834822988270125605842365589539690306474965584147981310997157542043256395776070485100881578291408250777738559790129129407309462785944505859412273194812753225152324801503466519048228961406646890305102510916237770448486230229488966711380555607956620732449373374027836767300203011615227008921843515652121379215748206859356920790214502277133099987729459596952817044582181956080965811702798062669891205061560742325686842271306295009864421853470810407128917646906550836129916694778023822502789667843489199409657361704586786242554006942516693979292624714524945408858422726153755260071904336329196375777502176005195800693847635789586878489536872122898557806826518192703632099480155874455575175312736471421295536494084385586615208012115079075068553344489258693283859653013272046970694571546959353658571788894862333292465202735853188533370948455403336565356988172582528918056635488363743793348411845580168331827676834646291995605513470039147876808640322629616641560667508153710646723108461964247537490553744805318226002710216400980584497526023035640038083472053149941172965736785066421400842696497103241919182121213206939769143923368374709228267738708132236680086924703491586840991153098315412063566123187504305467536983230827966457417620806593177265685841681837966106144963432544111706941700222657817358351259821080769101961052229263879745049019254311900620561906577452416191913187533984049343976823310298465893318373015809592522829206820862230332585280119266496314441316442773003237792274712330696417149945532261035475145631290668854345426869788447742981777493710117614651624183616680254815296335308490849943006763654806102940094693750609845588558043970485914449584445079978497045583550685408745163316464118083123079704389849190506587586425810738422420591191941674182490452700288263983057950057341711487031187142834184499153456702915280104485145176055306971441761368582384102787659324662689978418319620312262421177391477208004883578333569204533935953254564897028558589735505751235129536540502842081022785248776603574246366673148680279486052445782673626230852978265057114624846595914210278122788941448163994973881884622768244851622051817076722169863265701654316919742651230041757329904473537672536845792754365412826553581858046840069367718605020070547247548400805530424951854495267247261347318174742180078574693465447136036975884118029408039616746946288540679172138601225419503819704538417268006398820656328792839582708510919958839448297775647152026132871089526163417707151642899487953564854553553148754978134009964854498635824847690590033116961303766127923464323129706628411307427046202032013368350385425360313636763575212604707425311209233402837482949453104727418969287275572027615272268283376741393425652653283068469997597097750005560889932685025049212884068274139881631540456490350775871680074055685724021758685439053228133770707415830756269628316955687424060527726485853050611356384851965918968649596335568216975437621430778665934730450164822432964891270709898076676625671517269062058815549666382573829274182082278960684488222983394816670984039024283514306813767253460126007269262969468672750794346190439996618979611928750519442356402644303271737341591281496056168353988188569484045342311424613559925272330064881627466723523751234311893442118885085079358163848994487544756331689213869675574302737953785262542329024881047181939037220666894702204258836895840939998453560948869946833852579675161882159410981624918741813364726965123980677561947912557957446471427868624053750576104204267149366084980238274680575982591331006919941904651906531171908926077949119217946407355129633864523035673345588033313197080365457184791550432654899559705862888286866606618021882248602144999973122164138170653480175510438406624412822803616648904257377640956326482825258407669045608439490325290526337532316509087681336614242398309530806549661879381949120033919489494065132398816642080088395554942237096734840072642705701165089075196155370186264797456381187856175457113400473810762763014953309735174180655479112660938034311378532532883533352024934365979129341284854970946826329075830193072665337782559314331110963848053940859283988907796210479847919686876539987477095912788727475874439806779824968278272200926449944559380414608770641941810440758269805688038949654616587983904660587645341810289907194293021774519976104495043196841503455514044820928933378657363052830619990077748726922998608279053171691876578860908941817057993404890218441559791092676862796597583952483926734883634745651687016166240642424241228961118010615682342539392180052483454723779219911228595914191877491793823340010078128326506710281781396029120914720100947878752551263372884222353869490067927664511634758101193875319657242121476038284774774571704578610417385747911301908583877890152334343013005282797038580359815182929600305682612091950943737325454171056383887047528950563961029843641360935641632589408137981511693338619797339821670761004607980096016024823096943043806956620123213650140549586250615282588033022908385812478469315720323233601899469437647726721879376826431828382603564520699468630216048874528424363593558622333506235945002890558581611275341783750455936126130852640828051213873177490200249552738734585956405160830583053770732533971552620444705429573538361113677523169972740292941674204423248113875075631319078272188864053374694213842169928862940479635305150560788126366206497231257579019598873041195626227343728900516561111094111745277965482790471250581999077498063821559376885546498822938985408291325129076478386322494781016753491693489288104203015610283386143827378160946341335383578340765314321417150655877547820252454780657301342277470616744241968952613164274104695474621483756288299771804186785084546965619150908695874251184435837306590951460980451247409411373899927822492983367796011015387096129749705566301637307202750734759922943792393824427421186158236161317886392553095117188421298508307238259729144142251579403883011359083331651858234967221259621812507058113759495525022747274674369887131926670769299199084467161228738858457584622726573330753735572823951616964175198675012681745429323738294143824814377139861906716657572945807804820559511881687188075212971832636442155336787751274766940790117057509819575084563565217389544179875074523854455200133572033332379895074393905312918212255259833790909463630202185353848854825062897715616963860712382771725621313460549401770413581731931763370136332252819127547191443450920711848838366818174263342949611870091503049165339464763717766439120798347494627397822171502090670190302469762151278521956142070806461631373236517853976292092025500288962012970141379640038055734949269073535145961208674796547733692958773628635660143767964038430796864138563447801328261284589184898528048048844180821639423974014362903481665458114454366460032490618763039502356402044530748210241366895196644221339200757479128683805175150634662569391937740283512075666260829890491877287833852178522792045771846965855278790447562192663992008409302075673925363735628390829817577902153202106409617373283598494066652141198183810884515459772895164572131897797907491941013148368544639616904607030107596818933741217575988165127000761262789169510406315857637534787420070222051070891257612361658026806815858499852631465878086616800733264676830206391697203064894405628195406190685242003053463156621891327309069687353181641094514288036605995220248248886711554429104721929134248346438705368508648749099178812670565665387191049721820042371492740164460943459845392536706132210616533085662021188968234005752675486101476993688738209584552211571923479686888160853631615862880150395949418529489227074410828207169303387818084936204018255222271010985653444817207470756019245915599431072949578197878590578940052540122867517142511184356437184053563024181225473266093302710397968091064939272722683035410467632591355279683837705019855234621222858410557119921731717969804339317707750755627056047831779844447637560254637033369247114220815519973691371975163241302748712199863404548248524570118553342675264715978310731245663429805221455494156252724028915333354349341217862037007260315279870771872491234494477147909520734761385425485311552773301030342476835865496093722324007154518129732692081058424090557725645803681462234493189708138897143299831347617799679712453782310703739151473878692119187566700319321281896803322696594459286210607438827416919465162267632540665070881071030394178860564893769816734159025925194611823642945652669372203155504700213598846292758012527715422016629954863130324912311029627923723899766416803497141226527931907636326136814145516376656559839788489381733082668779901962886932296597379951931621187215455287394170243669885593888793316744533363119541518404088283815193421234122820030950313341050704760159987985472529190665222479319715440331794836837373220821885773341623856441380700541913530245943913502554531886454796252260251762928374330465102361057583514550739443339610216229675461415781127197001738611494279501411253280621254775810512972088465263158094806633687670147310733540717710876615935856814098212967730759197382973441445256688770855324570888958320993823432102718224114763732791357568615421252849657903335093152776925505845644010552192644505312073756287744998163646332835816140330175813967359427327690448920361880386754955751806890058532927201493923500525845146706982628548257883267398735220457228239290207144822219885587102896991935873074277815159757620764023951243860202032596596250212578349957710085626386118233813318509014686577064010676278617583772772895892746039403930337271873850536912957126715066896688493880885142943609962012966759079225082275313812849851526902931700263136328942095797577959327635531162066753488651317323872438748063513314512644889967589828812925480076425186586490241111127301357197181381602583178506932244007998656635371544088454866393181708395735780799059730839094881804060935959190907473960904410150516321749681412100765719177483767355751000733616922386537429079457803200042337452807566153042929014495780629634138383551783599764708851349004856973697965238695845994595592090709058956891451141412684505462117945026611750166928260250950770778211950432617383223562437601776799362796099368975191394965033358507155418436456852616674243688920371037495328425927131610537834980740739158633817967658425258036737206469351248652238481341663808061505704829059890696451936440018597120425723007316410009916987524260377362177763430621616744884930810929901009517974541564251204822086714586849255132444266777127863728211331536224301091824391243380214046242223349153559516890816288487989988273630445372432174280215755777967021666317047969728172483392841015642274507271779269399929740308072770395013581545142494049026536105825409373114653104943382484379718606937214444600826798002471229489405761853892203425608302697052876621377373594394224114707074072902725461307358541745691419446487624357682397065703184168467540733466346293673983620004041400714054277632480132742202685393698869787607009590048684650626771363070979821006557285101306601010780633743344773073478653881742681230743766066643312775356466578603715192922768440458273283243808212841218776132042460464900801054731426749260826922155637405486241717031027919996942645620955619816454547662045022411449404749349832206807191352767986747813458203859570413466177937228534940031631599544093684089572533438702986717829770373332806801764639502090023941931499115009105276821119510999063166150311585582835582607179410052528583611369961303442790173811787412061288182062023263849861515656451230047792967563618345768105043341769543067538041113928553792529241347339481050532025708728186307291158911335942014761872664291564036371927602306283840650425441742335464549987055318726887926424102147363698625463747159744354943443899730051742525110877357886390946812096673428152585919924857640488055071329814299359911463239919113959926752576359007446572810191805841807342227734721397723218231771716916400108826112549093361186780575722391018186168549108500885272274374212086524852372456248697662245384819298671129452945515497030585919307198497105414181636968976131126744027009648667545934567059936995464500558921628047976365686133316563907395703272034389175415267500915011198856872708848195531676931681272892143031376818016445477367518353497857924276463354162433601125960252109501612264110346083465648235597934274056868849224458745493776752120324703803035491157544831295275891939893680876327685438769557694881422844311998595700727521393176837831770339130423060958999137314684569010422095161967070506420256733873446115655276175992727151877660010238944760539789516945708802728736225121076224091810066700883474737605156285533943565843756271241244457651663064085939507947550920463932245202535463634444791755661725962187199279186575490857852950012840229035061514937310107009446151011613712423761426722541732055959202782129325725947146417224977321316381845326555279604270541871496236585252458648933254145062642337885651464670604298564781968461593663288954299780722542264790400616019751975007460545150060291806638271497016110987951336633771378434416194053121445291855180136575558667615019373029691932076120009255065081583275508499340768797252369987023567931026804136745718956641431852679054717169962990363015545645090044802789055701968328313630718997699153166679208958768572290600915472919636381673596673959975710326015571920237348580521128117458610065152598883843114511894880552129145775699146577530041384717124577965048175856395072895337539755822087777506072339445587895905719156736L

Ejercicios¶

Calcula la probabilidad de que dos enteros elegidos al azar uniformemente entre 1 y N sean primos entre sí. Hazlo de forma exacta y mediante una simulación.
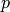Calcula la probabilidad de que una permutación $p$ de los enteros del 1 al 10 verifique 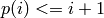$p(i)<=i+1$ . Hazlo de forma exacta y mediante una simulación.

Construcciones recursivas¶

Para enseñar combinatoria, puede ser interesante que los alumnos construyan los objetos en vez de simplemente usarlos.

Ejemplo resuelto : particiones de n con k partes fijas¶

Formas de descomponer un número n como suma de exactamente k enteros positivos.

Listamos los números de cada partición de mayor a menor, para evitar repeticiones.

Observamos que las particiones pertenecen a dos clases:

Las que terminan en 1.

Las que tienen todos sus elementos mayores o iguales a 2.

Esta idea nos permite construir las particiones recursivamente:

Generamos las particiones de n-1 en k-1 partes iguales, y añadimos un 1 al final para dar cuenta del primer grupo de particiones.

Generamos las particiones de n-k en k partes iguales, y sumamos 1 a cada elemento para dar cuenta del segundo grupo de particiones.

sage: def particiones(n, k):
...       if k == n:
...           return [[1]*n]
...       if k == 1:
...           return [[n]]
...       if not(0 < k < n):
...           return []
...       ls1 = [p+[1] for p in particiones(n-1, k-1)]
...       ls2 = [[parte+1 for parte in p] for p in particiones(n-k, k)]
...       return ls1 + ls2

sage: particiones(8,3)
[[6, 1, 1], [5, 2, 1], [4, 3, 1], [4, 2, 2], [3, 3, 2]]

Si sólo queremos contar el número de particiones de n con k elementos (en adelante 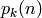$p_k(n)$ ), las reglas de recursión anteriores se traducen en la siguiente ecuación de recurrencia:

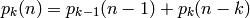
$p_k(n)=p_{k-1}(n-1) + p_k(n-k)$

junto con los “datos de frontera”:

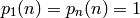
$p_1(n) = p_n(n)=1$

y:

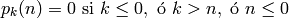
$p_k(n)=0 \text{ si } k\leq 0, \text{ ó } k > n, \text{ ó } n \leq 0$

sage: def n_particiones(n, k):
...       if k == n:
...           return 1
...       if k == 1:
...           return 1
...       if not(0 < k < n):
...           return 0
...       n1 = n_particiones(n-1, k-1)
...       n2 = n_particiones(n-k, k)
...       return n1 + n2

sage: n_particiones(8,3)
5

Se tarda menos tiempo en contar las posibilidades que en construirlas todas.

sage: time n_particiones(60,10)
62740
Time: CPU 0.92 s, Wall: 0.96 s

sage: time ls = particiones(60,10)
Time: CPU 19.84 s, Wall: 20.16 s

Cascadas de llamadas recursivas¶

Si aumentamos los parámetros, tarda mucho tiempo y consume mucha memoria.

El motivo es que llamamos muchas veces a la función con los mismos parámetros.

Lo veremos más claro con un ejemplo más sencillo:

sage: def fibo(n):
...       if n<2:
...           return 1
...       return fibo(n-1) + fibo(n-2)

.

Una llamada a fibo(3) hace una llamada a fibo(2) y otra a fibo(1).

fibo(2) hace otra llamada más a fibo(1), repitiendo el trabajo anterior.

El número de llamadas necesario crece de forma exponencial (de hecho, crece exactamente como los números de Fibonacci).

Solución rápida:

El decorador @cached_function altera una función para que almacene los valores de cada llamada

Evitamos calcular dos veces el valor de la función con los mismos argumentos.

La función debe ser determinista: a iguales argumentos, igual resultado.

sage: @cached_function
sage: def n_particiones_cached(n, k):
...       if k == n:
...           return 1
...       if k == 1:
...           return 1
...       if not(0 < k < n):
...           return 0
...       n1 = n_particiones_cached(n-1, k-1)
...       n2 = n_particiones_cached(n-k, k)
...       return n1 + n2

sage: time n_particiones_cached(60,10)
62740
Time: CPU 0.10 s, Wall: 0.12 s

Ejercicio (si hay tiempo)¶

Implementa la siguiente construcción recursiva de las combinaciones de n elementos tomadas de k en k elementos:

Si tienes una lista con n elementos y quieres todas las extracciones de k elementos (donde el orden no importa), contruye:

Las listas de k elementos extraídas de los n-1 primeros elementos de la lista original.

Toma las listas de k-1 elementos extraídas de los n-1 primeros elementos de la lista original, y añádeles el último elemento de la lista original.

Regresión¶

La regresión da mucho juego en clase:

Analizar datos reales
Probar conjeturas matemáticas
- ¿cuál es el orden de convergencia de esta sucesión?
- ¿cuántos primos hay en un intervalo de tal tipo lo bastante grande?
- ...

Analizamos una serie de datos extraída de un artículo de biología en el que se estudia el diámetro del ojo de distintos primates (D) como función de su peso (P):

sage: datos =[[0.3300, 12.544], [4.1850, 17.278], [2.9000, 17.979], [0.2000, 12.938],
...           [167.5000, 22.500], [72.3416, 24.521], [9.2500, 17.599], [6.0000, 19.176],
...           [51.5000, 19.000], [19.5100, 19.750], [0.1150, 8.070]]
sage: puntos = point(datos)
sage: var('P a b')
sage: D(P)=a*P^b
sage: parametros = find_fit(datos, D, solution_dict=True)
sage: print 'valores óptimos de los parámetros: ', parametros
valores óptimos de los parámetros:  {b: 0.10144858518005885, a:
14.368249010039623}

sage: Dstar = D.subs(parametros)
sage: error2 = sum((D0-Dstar(P=P0))^2 for P0,D0 in datos)/len(datos)
sage: print 'error cuadratico medio: %f'%error2
error cuadratico medio: 3.195483

sage: mindatos = min(x for x,y in datos)
sage: maxdatos = max(x for x,y in datos)
sage: ajuste = plot(Dstar, (x, mindatos, maxdatos), rgbcolor=(0,1,0))
sage: grafica = puntos + ajuste
sage: grafica.show()

.

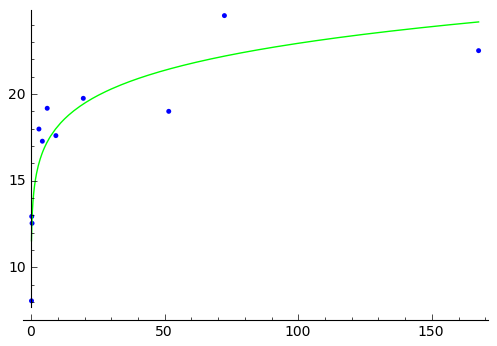
Si queremos trabajar con pocos datos, lo más sencillo es copiar y pegar.

Si tenemos muchos datos, podemos cargar el archivo usando el menú Data/Upload or create a file, y luego procesarlo usando las funciones de manejo de cadenas de python.

Si los datos están tabulados (por ej, csv), podemos:

usar las funciones de reemplazar de un editor de texto para dejarlo con la sintaxis de una lista de números de python (en ocasiones es conveniente usar expresiones regulares).

usar las instrucciones de manejo de cadenas de python (replace, split), y a menudo zip para unir listas.

Ejercicio¶

Crea un fichero de texto vacío

Corta y pega los siguientes datos (son datos de la temperatura de ebullición del agua a una cierta presión atmosférica, en unidades que no necesitamos saber):

T        P
194.5    20.79
194.3    20.79
197.9    22.4
198.4    22.67
199.4    23.15
199.9    23.35
200.9    23.89
201.1    23.99
201.4    24.02
201.3    24.01
203.6    25.14
204.6    26.57
209.5    28.49
208.6    27.76
210.7    29.04
211.9    29.88
212.2    30.06

A continuación:

Carga el fichero en una hoja de Sage vacía usando el menú ‘data’

Lee el fichero usando el comando open:

contenido = open(DATA + 'nombre_fichero').read()

.

Usa las instrucciones de manejo de cadenas de python para conseguir una lista de datos en el formato correcto (lista de tuplas de números).

Ajusta un modelo lineal a esos datos

Predice la temperatura de ebullición a a 27 mm HG de presión.

Distribucion discreta con soporte finito¶

Para la clase de probabilidad, podemos hacer algunos ejercicios con distribuciones de probabilidad discretas representando la función de masa mediante un diccionario en el que las claves son los puntos del espacio muestral y el valor asociado a cada clave es la probabilidad de ese punto. De esta forma, f[x] es la probabilidad asociada al punto x.

sage: #Ejemplos:
...
sage: #Bernouilli de prob p=1/3
sage: p = 1/3
sage: f_bernouilli = {0:p, 1:1-p}
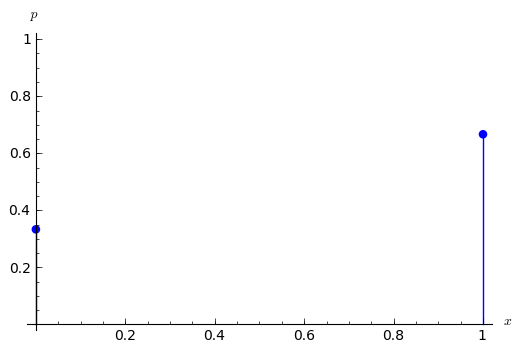
sage: #Binomial con prob p=1/3 y k=10 ensayos independientes
sage: k = 10
sage: p = 1/3
sage: f_binomial = dict((j, p^j*(1-p)^(k-j)*binomial(k,j)) for j in range(k+1))

Si el espacio muestral está contenido en 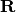$\RR$ , podemos dibujar la distribución por ejemplo así:

sage: #dibujar una distribucion discreta con soporte finito
sage: def dibuja_f(f, *args, **kargs):
...       '''Dibuja una funcion de masa con soporte finito, dada como diccionario
...
...       Acepta los argumentos adicionales tipicos de graficas en Sage,
...       como color, etc
...       '''
...       p = (sum([line2d([(x, 0), (x, f[x])], *args, **kargs) for x in f])
...            + point2d(f.items(), pointsize=30, *args, **kargs))
...
...       #Imponemos rango [0,1] para el eje que muestra las probabilidades
...       p.ymin(0)
...       p.ymax(1)
...       p.axes_labels(['$x$','$p$'])
...       return p

sage: show(dibuja_f(f_bernouilli))
sage: show(dibuja_f(f_binomial, color = (1,0,0)))

Esperanza y varianza de una variable aleatoria real:

sage: #media y varianza
sage: def media_f(f):
...       return sum(x*f[x] for x in f)
...
sage: def varianza_f(f):
...       m = media_f(f)
...       return sum((x-m)^2*f[x] for x in f)

sage: print media_f(f_bernouilli), varianza_f(f_bernouilli)
sage: print media_f(f_binomial), varianza_f(f_binomial)
2/3 2/9
10/3 20/9

y la función de distribución:

sage: F_binomial = dict((x, sum(p for y,p in f_binomial.items() if y<=x))
...                      for x in f_binomial)
sage: print F_binomial
{0: 1024/59049, 1: 2048/19683, 2: 5888/19683, 3: 11008/19683, 4: 15488/19683, 5: 18176/19683, 6: 2144/2187, 7: 19616/19683, 8: 19676/19683, 9: 59048/59049, 10: 1}

Ejercicio - debate : ¿Cómo podemos extraer un número en el soporte de nuestra función de masa respetando las probabilidades requeridas? Es decir, si tenemos:

f = {0:1/2, 1:1/3, 2:1/6}
valores   : [0, 1, 2]
cum_probs : [1/2, 5/6, 1]

queremos una función que devuelva 0 con probabilidad 1/2, 1 con probabilidad 1/3, y 2 con probabilidad 1/6.

Distribucion continua¶

Las distribuciones continuas se pueden manejar usando funciones simbólicas e integrales. Por ejemplo, la normal en una variable:

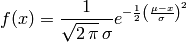
$f(x)=\frac{1}{\sqrt{2\, \pi }\,\sigma}e^{-\frac{1}{2}\left(\frac{\mu - x}{\sigma}\right)^2}$

sage: #Distribucion continua
sage: #Normal
sage: #funcion de densidad
sage: var('x')
sage: m = 0.7
sage: s = 1.4
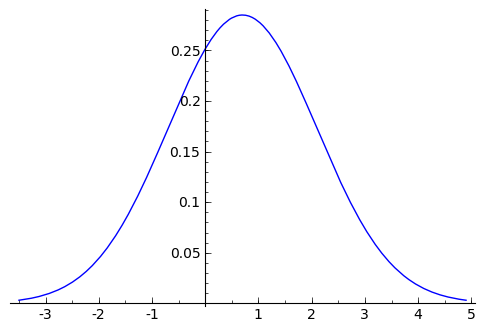
sage: f_normal = (1/sqrt(2*pi*s^2))*e^(-(x - m)^2/(2*s^2))
sage: #Un tipico dibujo de la normal, centrado en la media y con 3
sage: #desviaciones tipicas de rango
sage: show(plot(f_normal, x, m - 3*s, m + 3*s))

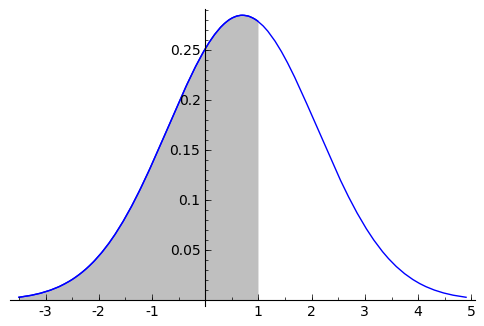
sage: #Probabilidad de que X<1, cuando X~N(0.7, 1.4)
sage: prob, error = numerical_integral(f_normal, -oo, 1)
sage: print prob
0.584837871172
sage: #Marcamos en el dibujo la prob pedida
sage: show(plot(f_normal, x, m - 3*s, m + 3*s) +
...        plot(f_normal, x, m - 3*s, 1, fill = True))

sage: #media y varianza
sage: def media_c(f):
...       return integral(x*f,x,-oo,oo)
...
sage: def varianza_c(f):
...       m = media_c(f)
...       return integral((x-m)^2*f,x,-oo,oo)

sage: media_c(f_normal), varianza_c(f_normal)
(0.7, 1.96)

Podemos usar variables simbólicas como parámetros.

sage: var('x mu sigma')
sage: assume(sigma > 0)  #necesario para las integrales simbolicas
sage: f_normal = (1/sqrt(2*pi*sigma^2))*e^(-(x - mu)^2/(2*sigma^2))
sage: media_c(f_normal), varianza_c(f_normal)
(mu, sigma^2)

Extracciones aleatorias¶

Para hacer extracciones aleatorias de una distribución continua es suficiente con obtener un p-cuantil con p arbitrario.

Para obtener un p-cuantil hay que invertir la función de distribución.

Si no es viable encontrar una solución simbólica, podemos hacerlo de forma numérica con find_root.

sage: #Extraccion aleatoria
sage: m = 0.7
sage: s = 1.4
sage: f_normal = (1/sqrt(2*pi*s^2))*e^(-(x - m)^2/(2*s^2))
sage: #1: extraemos un numero aleatorio entre 0 y 1
sage: t = random()
sage: #2: funcion de distribucion
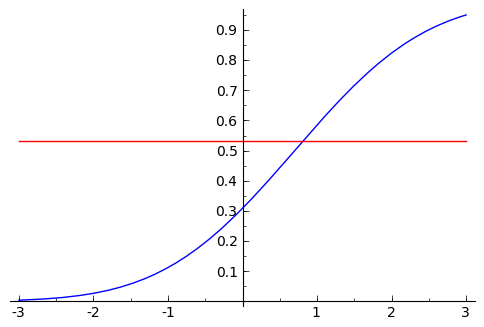
sage: var('x1')
sage: F_normal = integral(f_normal(x=x1), x1, -oo, x)
sage: show(plot(F_normal,x,-3,3) +
...        plot(0*x+t, x, -3, 3, color=(1,0,0)))
sage: #3: "invertimos" la funcion de distribucion (de forma numerica)
sage: print t, find_root(F_normal - t, m-10*s, m+10*s)
0.531001627926 0.808903109475

sage: #Intentar invertir la funcion de forma simbolica no funciona
sage: #con una normal (puede funcionar en otros casos)
sage: var('p')
sage: solve(F_normal==p, x)
[erf(5/14*sqrt(2)*x - 1/4*sqrt(2)) == 1/4853*(7777*sqrt(2)*p - 4853*e^(1/8))*e^(-1/8)]

sage: #extraccion aleatoria
sage: #el argumento es la funcion de distribucion, no la de densidad
sage: def extraccion_aleatoria_c(F):
...       t = random()
...       return find_root(F - t, -100, 100)

sage: extraccion_aleatoria_c(F_normal)
0.6299529113987602

Histograma¶

Para comparar una muestra aleatoria (una cantidad finita de puntos) con una distribución continua, tenemos que agrupar los datos extraídos en intervalos:

sage: from collections import defaultdict
sage: T = 400
sage: #Dividimos [-K,K] en N partes iguales
sage: K = 3
sage: N = 20
sage: frecuencias = defaultdict(int)
sage: for j in range(T):
...       a = extraccion_aleatoria_c(F_normal)
...       k = floor(a*N/(2*K))*(2*K/N)
...       frecuencias[k] += 1/(T*2*K/N)
sage: dibuja_f(frecuencias) + plot(f_normal, x, m-3*s, m+3*s, color=(1,0,0))

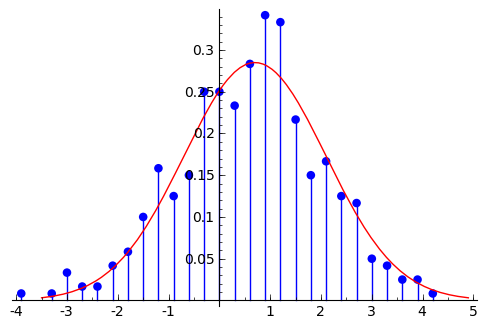
Por supuesto, mucha de esta funcionalidad está incluida en Sage

sage: #extracciones aleatorias de una normal
sage: normalvariate(0,1)
-1.2476798578721822

Ejercicio¶

Para hacer las extracciones aleatorias, hemos tenido que calcular los p-cuantiles tanto de una distribución finita como de una continua. Para distribuciones unidimensionales, la 1-distancia de Kantorovich (aka distancia de Wasserstein) de dos distribuciones de probabilidad es el promedio de las distancias entre los p-cuantiles correspondientes.

El teorema central del límite nos dice que si 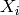$X_i$ son variables aleatorias independientes e idénticamente distribuidas, entonces la variable aleatoria

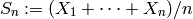
$S_n:=(X_1+\cdots+X_n)/n$

converge (para distintas nociones de convergencia), a una normal con la media y la varianza de 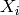$X_i$ .

Si $X_i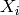$ siguen una distribución de Bernouilli con probabilidad 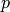$p$ , entonces 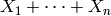$X_1+\cdots+X_n$ sigue una distribución binomial.

Aprende a escalar una distribución de probabilidad finita, para poder construir la distribución de $S_n$ .
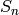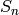Calcula de forma aproximada la distancia de Kantorovich entre $S_n$ y una normal de media 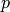$p$ y varianza $p(1-p)$ .

Distribución normal bidimensional¶

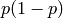Las distribuciones en más de una dimensión se manejan de forma similar, pero con más variables simbólicas. Por ejemplo, estudiamos la distribución normal en 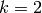$k=2$ dimensiones:

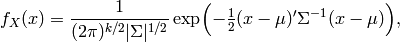
$f_X(x) = \frac{1}{ (2\pi)^{k/2}|\Sigma|^{1/2} } \exp\!\Big( {-\tfrac{1}{2}}(x-\mu)'\Sigma^{-1}(x-\mu) \Big),$

sage: #Normal bidimensional
sage: var('x1 x2')
sage: m1 = 1
sage: m2 = 0
sage: v1 = 3
sage: v12 = -2
sage: v2 = 4
sage: S = matrix(RDF, [[v1,v12],[v12,v2]])
sage: vs = vector([x1,x2])
sage: ms = vector([m1,m2])
sage: f = (1/(2*pi))*(1/sqrt(det(S)))*exp(-(1/2)*(vs-ms)*(~S)*(vs-ms))

sage: #plot3d(f,(x1,-3,3),(x2,-3,3)).show()
sage: p = contour_plot(f, (x1, m1-3*sqrt(v1), m1+3*sqrt(v1)), (x2, m2-3*sqrt(v2), m2+3*sqrt(v2)))
sage: p.show(aspect_ratio=1)

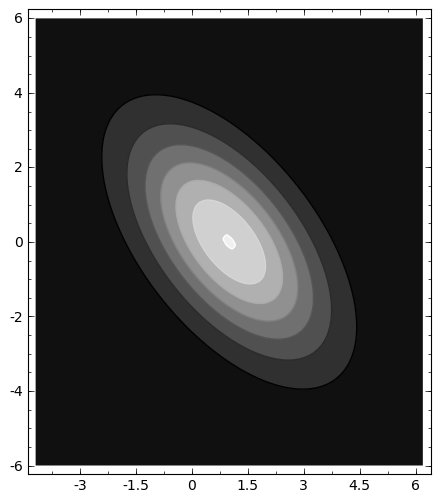
Resolvemos un típico ejercicio de probabilidad condicionada con dos variables normales: X=N(m=0.2,s=0.3) e Y=N(0.5, 0.6) son dos variables aleatorias que siguen una distribución normal, con cov(X,Y)=0.3.

Si sabemos que para un individuo (aka elemento del espacio muestral), Y=1.3, ¿cual es la prob de que X sea mayor que 0.10?

sage: var('x1 x2')
sage: m1 = 0.2
sage: m2 = 0.5
sage: v1  = 0.3
sage: v12 = 0.3
sage: v2  = 0.6
sage: S = matrix(RDF, [[v1,v12],[v12,v2]])
sage: vs = vector([x1,x2])
sage: ms = vector([m1,m2])
sage: f(x1,x2) = (1/(2*pi))*(1/sqrt(det(S)))*exp(-(1/2)*(vs-ms)*(~S)*(vs-ms))

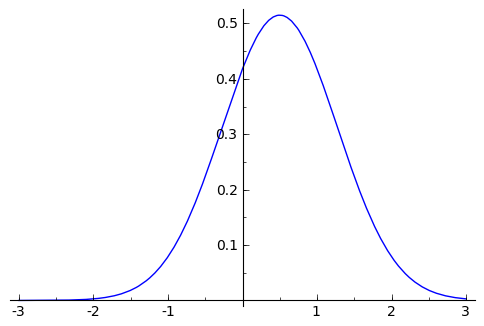
sage: f_marginal_2(x2)   = integral(f,x1,-oo,oo)
sage: f_condicionada_1_dado_2(x1,x2) = f(x1,x2)/f_marginal_2(x2)

sage: plot(f_marginal_2,x2, -3, 3)

sage: (plot(f_condicionada_1_dado_2(x2=1.3),x1, -3, 3) +
...    plot(f_condicionada_1_dado_2(x2=1.3),x1, -3, .1, fill=True))

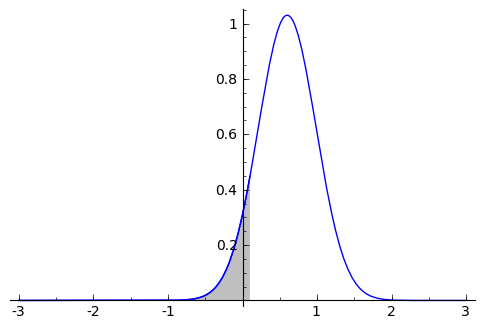
sage: numerical_integral(f_condicionada_1_dado_2(x2=1.3), -oo, 0.1)
(0.098352801229473263, 1.0996705400110192e-08)

Grafos¶

Si nos queda tiempo, veremos algo de grafos. Como calculo que no, y en realidad es muy fácil os remito a dos sesiones de trabajo de las notas de Laboratorio de Matemáticas:

Introducción a grafos en Sage : os llevará como mucho 20 minutos.

Grafos y malabares : incluye un poco de cadenas de Markov.

Un ejemplo breve:

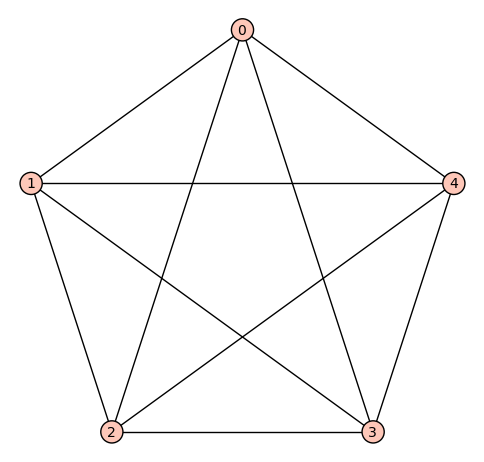
sage: g1 = graphs.CompleteGraph(5)
sage: print g1.is_connected()
True
sage: print g1.is_planar()
False
sage: print g1.is_eulerian()
True
sage: print g1.is_tree()
False
sage: show(g1.plot())

Para completar¶

Notas de laboratorio : bastante básico, pero ves un poco el panorama. En castellano, y con la licencia de la wikipedia, puedes cortar, pegar y usar en tu clase.

Libro de sage en francés : Tiene muy buena combinatoria, y algunos usos avanzados de los grafos (como emparejar personas y tareas). También tiene una licencia creative commons, pero lo tendrías que traducir.

Ayuda oficial de Sage : ya lo conocías, ¿verdad?

Ask sage : estupendo para dudas concretas.

Palabras finales¶

Muchas gracias por interesaros por Sage, en nombre de vuestros futuros ex-alumnos:

Mathematica, Matlab o Maple valen miles de euros

Sage se puede usar gratuitamente desde una página web (sagenb.org)

Tb se puede instalar donde tú quieras con las garantías del software libre.

Hay módulos de python para interaccionar con casi cualquier librería científica.

Ahora también hay un servidor de ipython, que puede ser más conveniente si no necesitas todo Sage.

Combinatoria, Probabilidad y Estadística con Sage¶

Breve resumen de las capacidades de Sage¶

R y Sage¶

Un primer ejemplo: lanzamientos de monedas¶

Objetos combinatorios¶

Ejemplos¶

Ejercicios¶

Construcciones recursivas¶

Ejemplo resuelto : particiones de n con k partes fijas¶

Cascadas de llamadas recursivas¶

Ejercicio (si hay tiempo)¶

Regresión¶

Ejercicio¶

Distribucion discreta con soporte finito¶

Distribucion continua¶

Extracciones aleatorias¶

Histograma¶

Ejercicio¶

Distribución normal bidimensional¶

Grafos¶

Para completar¶

Palabras finales¶

Table Of Contents

This Page

Navigation

Combinatoria, Probabilidad y Estadística con Sage¶

Breve resumen de las capacidades de Sage¶

R y Sage¶

Un primer ejemplo: lanzamientos de monedas¶

Objetos combinatorios¶

Ejemplos¶

Ejercicios¶

Construcciones recursivas¶

Ejemplo resuelto : particiones de n con k partes fijas¶

Cascadas de llamadas recursivas¶

Ejercicio (si hay tiempo)¶

Regresión¶

Ejercicio¶

Distribucion discreta con soporte finito¶

Distribucion continua¶

Extracciones aleatorias¶

Histograma¶

Ejercicio¶

Distribución normal bidimensional¶

Grafos¶

Para completar¶

Palabras finales¶

Table Of Contents

This Page

Quick search

Navigation