Una variable simbólica es un objeto en python que representa una incógnita que puede tomar cualquier valor. Por tanto, una operación que involucra una o más variables simbólicas no devuelve un valor numérico, sino una expresión simbólica que involucra números, operaciones, funciones y variables simbólicas. Si en algún momento sustituimos las variables simbólicas por números (o elementos de un anillo), podremos realizar las operaciones y obtener un número (o un elemento de un anillo).
Esta forma de trabajar se corresponde con los criterios de “no hacer las operaciones hasta el final”, “dejar las operaciones indicadas” y “cancelar términos antes de evaluar” que aprendistéis en secundaria.
sage: #Declaramos las variables a b c
sage: var('a b c')
sage: #Definimos varias expresiones simbolicas
sage: s = a + b + c
sage: s2 = a^2 + b^2 + c^2
sage: s3 = a^3 + b^3 + c^3
sage: s4 = a + b + c + 2*(a + b + c)
sage: p = a*b*c
sage: #Las imprimimos como código
sage: print s
sage: print s2
sage: print s3
sage: print s4
sage: print p
sage: #Las mostramos en el formato matemático usual
sage: show(s2)
sage: show(s3)
a + b + c
a^2 + b^2 + c^2
a^3 + b^3 + c^3
3*a + 3*b + 3*c
a*b*c
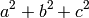
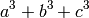
sage: #Sustituimos las variables por numeros
sage: print s(a=1, b=1, c=1)
sage: print s(a=1, b=2, c=3)
3
6
sage: #Operamos con las expresiones
sage: ex = (1/6)*(s^3 - 3*s*s2 +2*s3 )
sage: show(ex)
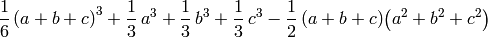
Sin embargo, pese a que no es posible evaluar una expresión hasta el final, observamos que al crear la expresión se han realizado “de oficio” algunas simplificaciones triviales. En ejemplos como el de arriba, nos puede interesar simplificar la expresión todavía más, pero es necesario decir qué queremos exactamente. Existen varias estrategias para intentar simplificar una expresión, y cada estrategia puede tener más o menos éxito dependiendo del tipo de expresión simbólica. Algunas estrategias dan lugar a una expresión más sencilla en algunos casos pero no en otros, y con expresiones complicada pueden consumir bastante tiempo de proceso.
Para la expresión anterior, como tenemos un polinomio, es buena idea expandirla en monomios que se puedan comparar unos con otros, usando el método expand .
sage: show(ex.expand())
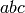
A menudo nos interesa lo contrario: factorizar la expresión usando factor .
sage: p = a^3 + a^2*b + a^2*c + a*b^2 + a*c^2 + b^3 + b^2*c + b*c^2 + c^3
sage: show(p)
sage: show(p.factor())
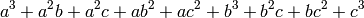
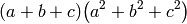
Si observas con el tabulador los métodos de las expresiones regulares, verás que hay métodos específicos para expresiones con funciones trigonométricas, exponenciales, con radicales o fracciones (es decir, con funciones racionales).
sage: p = sin(3*a)
sage: show(p.expand_trig())
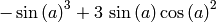
sage: p = sin(a)^2 - cos(a)^2
sage: show(p.simplify_trig())
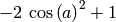
sage: p = 2^a * 4^(2*a)
sage: p.simplify_exp()
2^(5*a)
sage: p = 1/a - 1/(a+1)
sage: p.simplify_rational()
1/(a^2 + a)
A medio camino entre las expresiones simbólicas y las funciones de python, las funciones simbólicas son expresiones simbólicas en las que se fija el orden de las variables de entrada. Esto elimina la ambigüedad sobre qué variables se deben sustituir por qué argumentos y permite usarlas en sitios donde se espera una función de python.
sage: f(a,b,c) = a + 2*b + 3*c
sage: f(1,2,1)
8
sage: s = a + 2*b + 3*c
sage: s(1,2,1)
__main__:4: DeprecationWarning: Substitution using function-call syntax and unnamed arguments is deprecated and will be removed from a future release of Sage; you can use named arguments instead, like EXPR(x=..., y=...)
8
En algunos aspectos las expresiones simbólicas pueden parecer similares a los polinomios que vimos en el bloque III, lo que puede provocar confusión. Es importante saber si tenemos entre manos una expresión simbólica que representa un polinomio como ésta:
var('x')
p = x^2 + 1
o un polinomio como éste (con coeficientes por ejemplo en RDF ):
R.<t> = PolynomialRing(RDF)
q = t^2 + 1
Aunque ambos tienen métodos de propósito similar como coefficients o roots , el comportamiento es distinto, a veces de manera obvia y a veces de manera más sutil. Por ejemplo, las raíces o los coeficientes de una expresión simbólica son a su vez expresiones simbólicas, mientras que en el caso de un polinomio son miembros del anillo de coeficientes.
sage: var('x')
sage: p = x^2 + 3
sage: print p.coefficients()
sage: print p.roots()
sage: termino_indi = p.coefficients()[0][0]
sage: print termino_indi, parent(termino_indi)
[[3, 0], [1, 2]]
[(-I*sqrt(3), 1), (I*sqrt(3), 1)]
3 Symbolic Ring
sage: R.<t> = PolynomialRing(RDF)
sage: q = t^2 + 3
sage: print q.coefficients()
sage: print q.roots()
sage: termino_indi = q.coefficients()[0]
sage: print termino_indi, parent(termino_indi)
[3.0, 1.0]
[]
3.0 Real Double Field
El método polynomial permite construir un polinomio con coeficientes en un anillo dado a partir de una expresión simbólica. Para hacer lo contrario, podemos sustituir la variable del anillo de polinomios por una variable simbólica, o convertir explícitamente al tipo de datos SR (el anillo de expresiones simbólicas, o Symbolic Ring).
sage: p.polynomial(ZZ).roots()
[]
sage: q0 = q(t=x); q0
x^2 + 3.0
sage: q1 = SR(q); q1
t^2 + 3.0
Si usamos el operador de igualdad (==) o algún operador de comparación (<, <=, >, >=, !=) sobre dos expresiones simbólicas, obtenemos una relación simbólica. Al igual que las expresiones simbólicas, las operaciones en una relación están indicadas pero no se pueden ejecutar hasta que todas las variables han tomado un valor concreto.
Para evaluar la relación y obtener un booleano, usamos el operador de conversión a booleano bool(relacion) . Algunas relaciones tienen un valor definido, incluso aunque dependan de variables simbólicas: son siempre ciertas o siempre falsas. Muchas otras tendrán un valor indeterminado: dependiendo de los valores de las variables. En estos casos, el valor booleano de la relación es False , siguiendo una convención usual en otros programas de cálculo simbólico. También obtenemos False si evaluamos una expresión demasiado compleja para el motor simbólico. Tomamos buena nota de la asimetría en los resultados:
- True : el programa puede demostrar que la relación se verifica siempre, para cualquier valor de las variables.
- False : el programa no puede demostrar que la relación se verifica siempre, para cualquier valor de las variables. Eso no significa que nunca se verifique, ni siquiera que sea ambigua (cierta para algunos valores de las variables y falsa para otros).
sage: var('a b')
sage: r1 = (a<a+1)
sage: r2 = (a<a-1)
sage: r3 = (a<b)
sage: r4 = (b<a)
sage: r5 = a > 0
sage: print bool(r1), bool(r2), bool(r3), bool(r4), bool(r5)
True False False False False
Para distinguir entre relaciones que se puede demostrar que son falsas y relaciones ambiguas (o demasiado complicadas para el software), podemos usar la negación de las relaciones. Vemos por ejemplo, que se puede demostrar que r2 es siempre falsa porque su negación se resuelve a True .
sage: print r2.negation(), bool(r2.negation())
sage: print r3, bool(r3)
sage: print r3.negation(), bool(r3.negation())
a >= a - 1 True
a < b False
a >= b False
Por supuesto concretando los valores de algunas variables, una relación ambigua se puede concretar, y resultar cierta (o falsa).
sage: print bool(r2(a=1, b=2)), bool(r3(a=1, b=2))
sage: print bool(r2(a=3, b=2)), bool(r3(a=3, b=2))
sage: print bool(r5(a=e^b))
False True
False False
True
Aparte de preguntar por su valor de verdad, podemos simplificar y operar con las relaciones de forma similar a las formas de operar con una expresión cualquiera:
sage: r1 = (a<a+1)
sage: print r1.subtract_from_both_sides(a)
0 < 1
sage: print r3
sage: print r4
sage: r6 = r3 + r4
sage: print r6
sage: r6 = r6.subtract_from_both_sides(r6.right_hand_side())
sage: print r6
a < b
b < a
a + b < a + b
0 < 0
El comando solve permite resolver ecuaciones (al menos lo intenta): para resolver una ecuación llamamos a solve con la ecuación como primer argumento y la variable a despejar como segundo argumento, y recibimos una lista con las soluciones.
sage: x = var('x')
sage: solve(x^2 + 3*x + 2 == 0, x)
[x == -2, x == -1]
Si en vez de pasar una igualdad pasamos una expresión r , calcula las soluciones de r==0 .
sage: #Las soluciones de esta ecuacion cubica son numeros complejos
sage: solve(x^3 - 3*x + 5, x)
[x == -1/2*(1/2*sqrt(21) - 5/2)^(1/3)*(I*sqrt(3) + 1) - 1/2*(-I*sqrt(3) + 1)/(1/2*sqrt(21) - 5/2)^(1/3), x == -1/2*(1/2*sqrt(21) - 5/2)^(1/3)*(-I*sqrt(3) + 1) - 1/2*(I*sqrt(3) + 1)/(1/2*sqrt(21) - 5/2)^(1/3), x == (1/2*sqrt(21) - 5/2)^(1/3) + 1/(1/2*sqrt(21) - 5/2)^(1/3)]
A veces solve no puede resolver la ecuación, en cuyo caso puede que la simplifique un poco, o ni siquiera éso.
sage: solve(x^5 + 4*x^3 == x^3 + 2, x)
[0 == x^5 + 3*x^3 - 2]
Ante una ecuación arbitraria de quinto grado, podemos intentar encontrar las soluciones de forma numérica (volveremos a hablar de este tema).
sage: soluciones = solve(x^5 + 4*x^3 == x^3 + 2, x)
sage: s = soluciones[0]
sage: print s
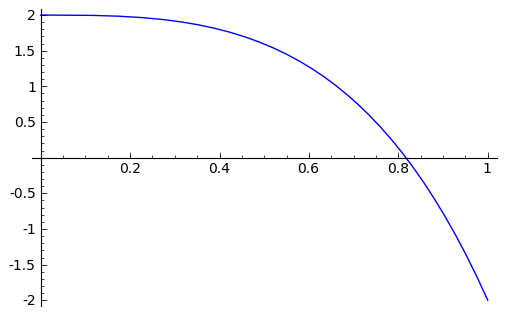
sage: show(plot(s, x, 0, 1)) #dibujamos s entre 0 y 1
sage: print s.find_root(0,1) #buscamos una raiz (numerica) entre 0 y 1
0 == x^5 + 3*x^3 - 2
0.816997207347
solve trabaja con expresiones con muchas variables simbólicas, e intenta despejar la variable que le pasamos como argumento y expresarla como función de las otras
sage: var('x y')
sage: for expresion in solve(x^4 + y^2*x^2 + 2, x ):
... show(expresion)
sage: for expresion in solve(x^4 + y^2*x^2 + 2, y ):
... show(expresion)
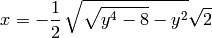
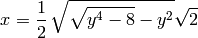
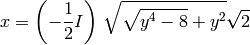
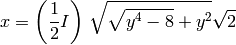
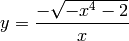
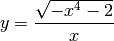
También podemos usar solve para resolver sistemas de ecuaciones (lineales o no). Como primer argumento pasamos una lista de ecuaciones y después sigue la lista de variables que queremos despejar.
Aplicar solve a sistemas lineales de ecuaciones es totalmente equivalente a resolver el sistema mediante matrices , aunque las distintas posibilidades (incompatible, compatible determinado...) se muestran de forma distinta.
sage: var('x1 x2 x3')
(x1, x2, x3)
sage: #Compatible determinado
sage: #Resolvemos el sistema usando solve
sage: eq1 = 2*x1 + x3 == 1
sage: eq2 = x1 + x2 - x3 == 0
sage: eq3 = -x1 -2*x2 == -1
sage: print solve([eq1,eq2,eq3],x1,x2,x3)
sage: #Resolvemos el sistema usando matrices
sage: M = matrix(QQ,3,3,[2,0,1, 1,1,-1, -1,-2,0 ])
sage: v = vector(QQ,[1,0,-1])
sage: M.solve_right(v ) #tambien vale M\v
[
[x1 == (1/5), x2 == (2/5), x3 == (3/5)]
]
(1/5, 2/5, 3/5)
sage: #Compatible indeterminado
sage: #Resolvemos el sistema usando solve
sage: eq1 = 2*x1 + x3 == 1
sage: eq2 = x1 + x2 - x3 == 0
sage: print solve([eq1,eq2],x1,x2,x3)
sage: #Resolvemos el sistema usando matrices
sage: M = matrix(QQ,2,3,[2,0,1, 1,1,-1])
sage: v = vector(QQ,[1,0])
sage: #solve_right solo encuentra una solucion
sage: print M.solve_right(v ) #tambien vale M\v
sage: print M.right_kernel()
[
[x1 == -1/2*r1 + 1/2, x2 == 3/2*r1 - 1/2, x3 == r1]
]
(1/2, -1/2, 0)
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -3 -2]
sage: #Incompatible
sage: #solve devuelve silenciosamente una lista de soluciones vacia
sage: eq1 = 2*x1 + x3 == 1
sage: eq2 = x1 + x2 - x3 == 0
sage: eq3 = x1 + x2 - x3 == 1
sage: print solve([eq1,eq2,eq3],x1,x2,x3)
sage: #M\v, o M.solve_right(v) arrojan un error
sage: M = matrix(QQ,3,3,[2,0,1, 1,1,-1, 1,1,-1])
sage: v = vector(QQ,[1,0,1])
sage: M\v
[
]
Traceback (most recent call last):
...
ValueError: matrix equation has no solutions
El comando asume informa a Sage de que cierta identidad no trivial que involucra algunas variables simbólicas se verifica. Esto es importante porque permite hacer ciertas simplificaciones extra. Por ejemplo:
sage: var("x")
sage: s = sqrt(x^2)
sage: simplify(s)
sqrt(x^2)
sage: assume(x>0)
sage: simplify(s)
x
El comando dual de assume es forget , que olvida una identidad que anteriormente habíamos asumido como cierta (la sintaxis es idéntica).
forget() sin argumentos olvida todas las identidades.
assumptions() muestra todas las identidades activas.
sage: assumptions()
[x > 0]
sage: forget(x>0)
sage: simplify(s)
sqrt(x^2)
sage: assumptions()
[]
También podemos asumir otro tipo de información, como por ejemplo que una variable representa un número entero.
sage: var('n')
sage: assume(n, 'integer')
sage: print sin(n*pi).simplify()
sage: forget(n, 'integer')
sage: print sin(n*pi).simplify()
0
sin(pi*n)
sage: var('k t')
sage: assume(k, 'integer')
sage: simplify(sin(t+2*k*pi))
sin(t)
Si tomamos por ciertas varias identidades incompatibles, Sage lanza un error:
sage: var('x')
sage: forget()
sage: assume(x<0)
sage: assume(x>0)
Traceback (most recent call last):
...
ValueError: Assumption is inconsistent
Si usamos el anillo de expresiones simbólicas ( SR ) para los coeficientes de las matrices, podemos trabajar con parámetros.
sage: #Ejemplo de una matriz dependiendo de un parámetro
sage: var('a')
sage: M = matrix(SR,3,3, [1,2,3, 1,-3,1, 2,1,a])
sage: M
[ 1 2 3]
[ 1 -3 1]
[ 2 1 a]
sage: #Ejemplo: la matriz de van der Monde 3x3
sage: var('a1 a2 a3')
sage: VDM = matrix([[1, a1, a1^2], [1, a2, a2^2], [1, a3, a3^2] ])
sage: show(VDM)
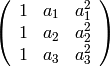
Ejercicio resuelto: Calcula el rango de la matriz
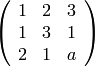
dependiendo del valor del parámetro a .
sage: var('a')
sage: M = matrix(SR,3,3, [1,2,3, 1,-3,1, 2,1,a])
sage: M
[ 1 2 3]
[ 1 -3 1]
[ 2 1 a]
Solución 1: ponemos la matriz en forma escalonada mediante operacinoes de fila y vemos que el rango depende de si a es 24/5 o no.
sage: M.add_multiple_of_row(1,0,-1)
sage: M
[ 1 2 3]
[ 0 -5 -2]
[ 2 1 a]
sage: M.add_multiple_of_row(2,0,-2)
sage: M
[ 1 2 3]
[ 0 -5 -2]
[ 0 -3 a - 6]
sage: M.add_multiple_of_row(2,1,-3/5)
sage: M
[ 1 2 3]
[ 0 -5 -2]
[ 0 0 a - 24/5]
Por supuesto, también podemos calcular el determinante
sage: var('a')
sage: M = matrix(SR,3,3, [1,2,3, 1,-3,1, 2,1,a])
sage: determinante = M.det()
sage: determinante.factor()
-5*a + 24
Sin embargo, la forma escalonada produce un resultado inesperado: como las expresiones simbólicas no nulas son invertibles, la matriz es equivalente a la identidad!
sage: M.echelon_form()
[1 0 0]
[0 1 0]
[0 0 1]
Encuentra la recta afín que pasa por el punto 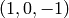 y corta a las rectas
y corta a las rectas 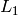 y
y 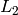 , sabiendo que
, sabiendo que 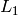 pasa por
pasa por 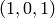 y
y 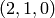 , y que
, y que 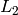 pasa por
pasa por 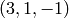 y
y 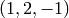 .
.
sage: p1 = vector([1,0,1])
sage: p2 = vector([2,1,0])
sage: p3 = vector([3,1,-1])
sage: p4 = vector([1,2,-1])
sage: p5 = vector([1,0,-1])
sage: var('r s t')
sage: #Calculamos un punto generico de L1, y otro de L2
sage: pgL1 = (1-r)*p1+r*p2
sage: pgL2 = (1-s)*p3+s*p4
sage: #Un punto generico de la recta que pasa por pgL1 y pgL2
sage: pgL = (1-t)*pgL1 + t*pgL2
sage: pgL
(-(t - 1)*(r + 1) - (2*s - 3)*t, -(t - 1)*r + (s + 1)*t, (t - 1)*(r - 1) - t)
sage: #Imponemos las ecuaciones que representan que
sage: eqs = [c1==c2 for c1,c2 in zip(pgL,p5)]
sage: print eqs
sage: solve(eqs,r,s,t)
[-(t - 1)*(r + 1) - (2*s - 3)*t == 1, -(t - 1)*r + (s + 1)*t == 0, (t - 1)*(r - 1) - t == -1]
[[r == 2, s == (1/3), t == 3]]
La recta pasa por p5 y por (1-r)*p1+r*p2, con r=2, es decir 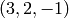
sage: ((1-r)*p1+r*p2)(r=2)
(3, 2, -1)
Ejercicio: encuentra las ecuaciones implícitas y paramétricas de la recta solución
Si vas a evaluar muchas veces una expresión simbólica, puedes “compilarla” usando el comando fast_float , que devuelve una función normal de python correspondiente a la expresión simbólica. Esta función ya no se puede manipular de forma simbólica, pero se puede evaluar usando mucho menos tiempo.
sage: var('a b c')
sage: f(a,b,c) = a^3 + sin(b + 3*log(c))
sage: timeit('f(1,2,1)')
sage: ff = fast_float(f)
sage: timeit('ff(1,2,1)')
625 loops, best of 3: 248 µs per loop
625 loops, best of 3: 13 µs per loop
sage: var('a b c')
sage: s = a^3 + sin(b + 3*log(c))
sage: timeit('s(a=1, b=2, c=1)')
sage: fs = fast_float(s, a, b, c)
sage: timeit('fs(1,2,1)')
625 loops, best of 3: 109 µs per loop
625 loops, best of 3: 13 µs per loop