Aproxima el número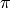 
por el método de Monte Carlo
Genera pares (x,y) de números aleatorios entre -1 y 1. Estos pares de números están escogidos en el cuadrado [-1,1]x[-1,1] de forma uniforme. Si contamos el ratio de los pares (x,y) tales que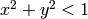 
entre el total de pares, obtenemos el área del círculo unidad dividido entre el área del cuadrado unidad.
- Utiliza esta idea para aproximar el número
Estima mediante el método de Monte Carlo las probabilidades de diversos eventos relacionados con lanzamientos de monedas que calculaste en el ejercicio de la sección 1.
Los paquetes de cereales ACME traen seis tipos distintos de regalos. Fulanito está dispuesto a comprar cajas de cereales hasta tenerlos todos.
Asumiendo que la probabilidad de encontrar cada tipo de regalo en una caja de cereales es la misma, e independiente de las otras cajas de cereales, estima mediante el método de Monte Carlo el número de cajas que tendrá que comprar Fulanito hasta tener al menos un regalo de cada tipo.
Estima mediante el método de Monte Carlo la probabilidad de que en un grupo de 30 personas, al menos dos de ellas cumplan años el mismo día.
Para ello, asume que cada persona del grupo tiene un cumpleaños elegido aleatoriamente entre 1 y 365, y que el cumpleaños de cada uno es independiente del cumpleaños de los demás.
Nota: es posible resolver este problema por razonamiento, pero no por fuerza bruta. El número de posibles fechas de cumpleaños para las 30 personas es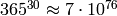 
.
Generamos un grafo aleatorio de la forma siguiente: partimos de un conjunto de k vértices y, con probabilidad p , ponemos una arista entre cada dos vértices, haciendo cada elección de forma independiente. Nos preguntamos cuál es la probabilidad de obtener un grafo con una cierta propiedad.
- Calcula la probabilidad de obtener un grafo plano cuando k=6, p=0.6 y cuando k=12, p=0.3.
- Calcula la probabilidad de obtener un grafo conexo cuando k=6, p=0.5.
Indicación : construye la matriz de incidencia de forma aleatoria, con las entradas 0 y 1. Ten cuidado, porque la matriz debe ser simétrica. Si decides que entre los vértices j y k debe haber una arista, tienes que poner unos en las entradas M[j,k] y M[k,j] de la matriz de incidencia. Alternativamente, busca código en Sage que genera estos grafos.
