En esta lección vamos a estudiar las posibilidades que ofrece SAGE para trabajar con grafos .
Un grafo consiste de un conjunto de vértices y otro conjunto de aristas que unen algunos de los vértices. En un grafo no dirigido las aristas no tienen dirección, mientras que en los grafos dirigidos debemos distinguir entre la arista que une el vértice v1 con el v2 de la arista que une el vértice v2 con el v1.
Existen constructores para muchos de los grafos no dirigidos más famosos, dentro del módulo graphs . Por ejemplo:
- Grafo completo: el que tiene todas las aristas que unen cada par de vértices
- Grafo cíclico: una circuito simple
- Grafo del n-cubo
- ...
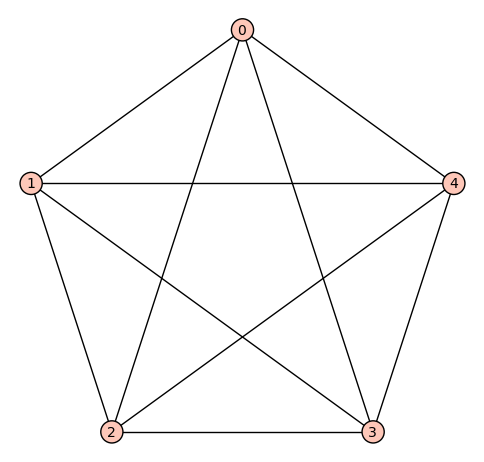
sage: g1 = graphs.CompleteGraph(5)
sage: show(g1.plot())
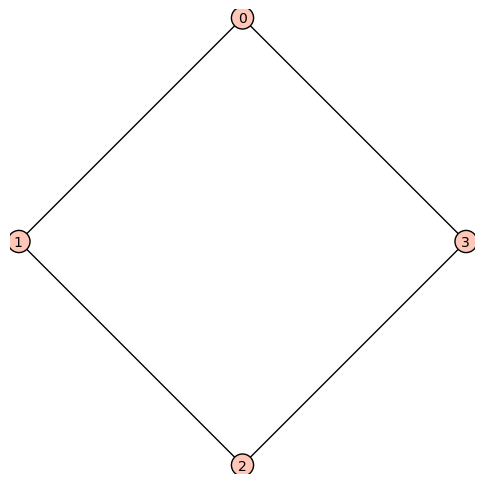
sage: g2 = graphs.CycleGraph(4)
sage: show(plot(g2))
sage: g3 = graphs.CubeGraph(3)
sage: show(plot(g3))
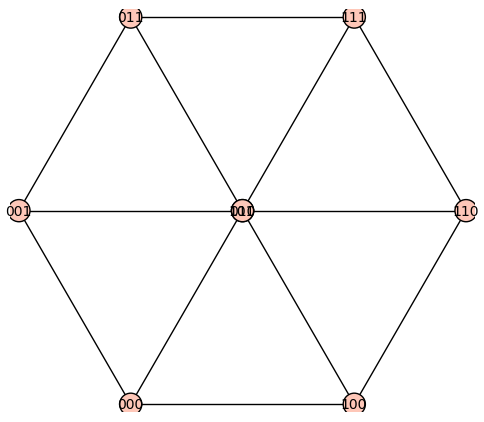
El dibujo anterior confunde dos de los vértices. Leemos la documentación de Graph.plot para encontrar la forma de mejorar el dibujo
sage: g3.plot?
<html>...</html>
sage: #Una solucion: usar otro "layout"
sage: show(plot(g3, layout='spring'))
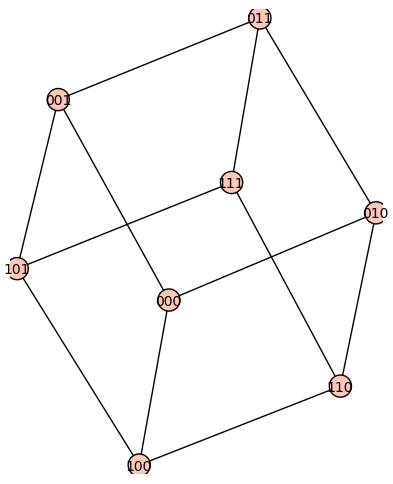
Como de costumbre, usando el tabulador accedemos a una lista completa con todos los grafos disponibles.
sage: graphs.
Traceback (most recent call last):
...
SyntaxError: invalid syntax
También tenemos alguns familias de grafos famosos en la librería digraphs .
sage: show(plot(digraphs.Circuit(5)))
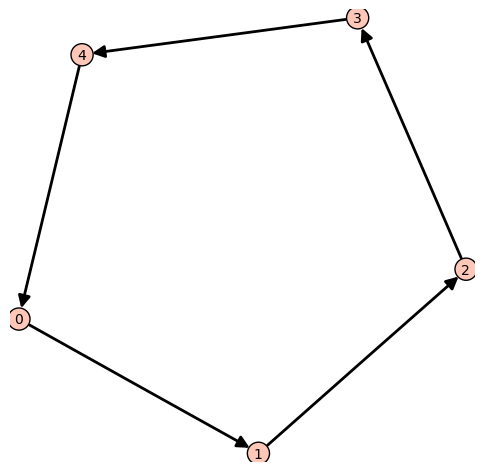
..index:: Graph, matriz de adyacencia, DiGraph
También podemos introducir un grafo usando la matriz de adyacencia : una matriz KxK (donde K es el número de vértices), que tiene un 1 en la posición i,j si y sólo si hay una arista entre los vértices i y j . Para grafos no dirigidos, la matriz debe ser simétrica.
Nota : En la documentación de Graph puedes encontrar otras formas de introducir un grafo (por ejemplo, mediante un diccionario asigna a cada vertice la lista de sus vecinos).
sage: M = matrix([[0,1,0,0],[1,0,0,0],[0,0,0,1],[0,0,1,0]])
sage: show(M)
sage: g4 = Graph(M)
sage: show(g4, layout='circular')
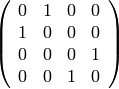
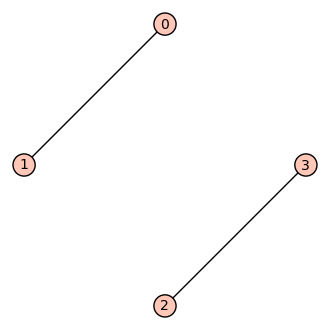
Podemos construir del mismo modo un grafo dirigido, con una matriz no necesariamente simétrica, usando DiGraph .
sage: M = matrix(ZZ,[[0,0,0,0],[1,0,0,0],[0,0,0,1],[0,0,1,0]])
sage: show(M)
sage: g4 = DiGraph(M)
sage: show(g4, layout='circular')
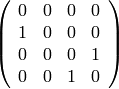
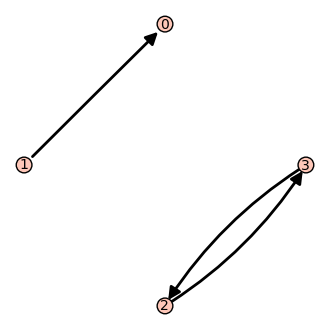
El método adjacency_matrix devuelve la matriz de adyacencia de un grafo, independientemente de cómo lo introdujimos.
sage: g1.adjacency_matrix()
[0 1 1 1 1]
[1 0 1 1 1]
[1 1 0 1 1]
[1 1 1 0 1]
[1 1 1 1 0]
También podemos construir nuevos grafos a partir de otros.
- La suma de grafos devuelve la unión de los dos grafos.
- El producto de un grafo por un entero repite un grafo.
sage: g5 = g1 + g2
sage: show(g5,layout='circular')
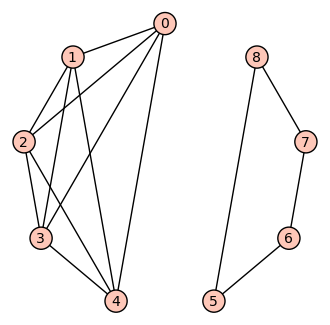
sage: g6 = g4*3
sage: show(g6,layout='circular')
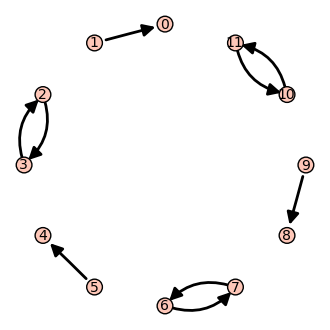
Podemos añadir y quitar vértices y aristas a grafos existentes usando add_vertex , add_edge , delete_vertex , delete_edge .
sage: g7 = 2*g2
sage: show(g7,layout='spring')
sage: g7.add_edge(0,4)
sage: g7.add_edge(1,5)
sage: g7.add_edge(2,6)
sage: g7.add_edge(3,7)
sage: show(g7,layout='spring')
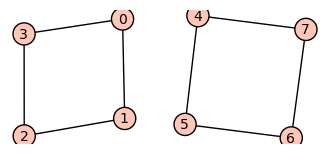
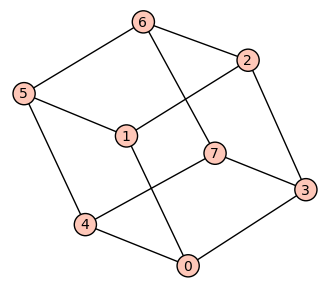
Podemos partir de un grafo vacío y añadir los vértices y aristas necesarios:
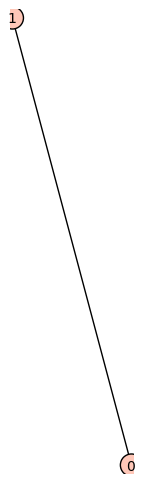
sage: g8 = Graph()
sage: g8.add_vertex(0)
sage: g8.add_vertex(1)
sage: g8.add_edge(0,1)
sage: plot(g8)
Modifica el grafo g6 añadiendo un vértice y uniendo todos los otros vértices al nuevo vértice.
Podemos verificar un buen número de propiedades de un grafo usando los métodos adecuados. Por ejemplo:
- is_connected : comprueba si el grafo es conexo
- is_planar : comprueba si el grafo es plano . Un grafo es plano si se pueden dibujar los vértices y las aristas en un plano sin que las aristas se intersequen.
- is_eulerian : comprueba si el grafo tiene un circuito euleriano . Un circuito en un grafo es una sucesión de aristas adyacentes que comienza y termina en el mismo vértice. Un circuito euleriano es un circuito que pasa exactamente una vez por cada arista.
- is_tree : comprueba si el grafo es un árbol . Un árbol es un grafo conexo que no tiene ningún circuito cerrado .
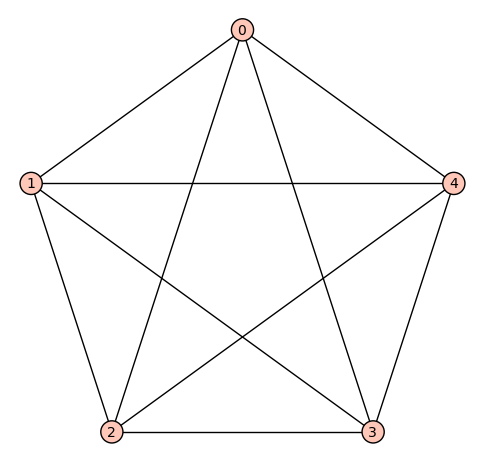
sage: print g1.is_connected()
sage: print g1.is_planar()
sage: print g1.is_eulerian()
sage: print g1.is_tree()
sage: show(g1.plot())
True
False
True
False
Dos grafos son isomorfos si y sólo si existe una biyección del conjunto de vértices del primero en el conjunto de vértices del segundo tal que dos vértices están unidos en el primer grafo si y sólo si los vértices correspondientes están unidos en el segundo.
En dos grafos isomorfos, los vértices pueden tener nombres distintos y estar colocados en distintas posiciones, pero todas las relaciones de incidencia y todas las propiedades de grafos como conexión, planaridad etćetera son idénticas.
sage: print g7.is_isomorphic(g3)
sage: print g7 == g3
sage: print g3.vertices()
sage: print g7.vertices()
True
False
['000', '001', '010', '011', '100', '101', '110', '111']
[0, 1, 2, 3, 4, 5, 6, 7]
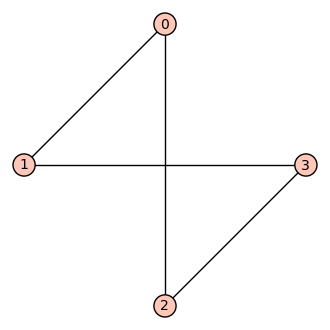
Pregunta: ¿cuál de los grafos que definimos antes es isomorfo al siguiente grafo?
sage: M = matrix(ZZ,[[0,1,1,0],[1,0,0,1],[1,0,0,1],[0,1,1,0]])
sage: show(M)
sage: g9=Graph(M)
sage: show(g9,layout='circular')
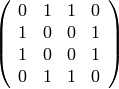
La función graphs genera un grafo de cada clase de isomorfismo de grafos con un cierto número de vértices.
sage: for g in graphs(4):
... if g.is_connected():
... print g.adjacency_matrix()
... print
[0 1 1 1]
[1 0 0 0]
[1 0 0 0]
[1 0 0 0]
[0 1 1 0]
[1 0 0 0]
[1 0 0 1]
[0 0 1 0]
[0 1 1 0]
[1 0 1 0]
[1 1 0 1]
[0 0 1 0]
[0 1 1 0]
[1 0 0 1]
[1 0 0 1]
[0 1 1 0]
[0 1 1 0]
[1 0 1 1]
[1 1 0 1]
[0 1 1 0]
[0 1 1 1]
[1 0 1 1]
[1 1 0 1]
[1 1 1 0]
sage: L = list(graphs(4))
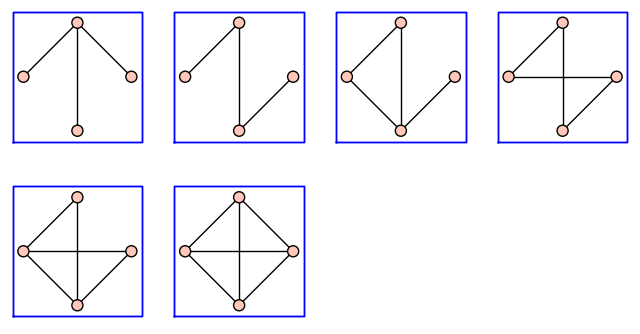
El siguiente método es una forma de dibujar un montón de grafos en poco espacio.
sage: graphs_list.show_graphs(L)
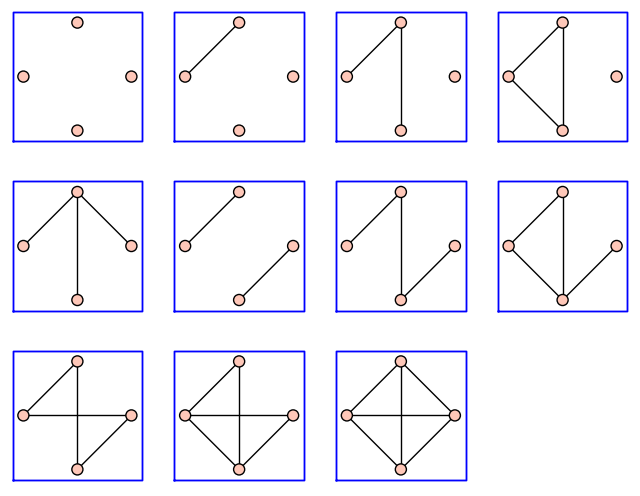
Podemos generar todos los grafos con un cierto número de vértices y contar el número de ellos que verifican una cierta propiedad.
sage: L = [g for g in graphs(4) if g.is_connected()]
sage: print len(L)
sage: graphs_list.show_graphs(L)
6