Buena parte de los siguientes ejercicios están extraídos de las hojas de problemas de Álgebra Lineal.
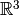. Si lo es, encuentra las coordenadas en la nueva base de 
.
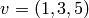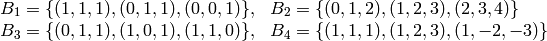
Escribe una función que acepte como argumento una lista de vectores, y te devuelva un subconjunto maximal de vectores linealmente independientes extraídos de la lista anterior. El método consiste en recorrer la lista, y quedarte sólo con los vectores que son linealmente independientes con los vectores que has elegido antes.
Ejemplos:
{(1,0,0),(2,0,0),(1,1,0),(0,1,0),(2,1,0)} \-> {(1,0,0),(1,1,0)}
{(1,0,0),(1,0,1),(2,0,0),(1,1,0),(0,1,0),(2,1,0),(0,0,1)} \-> {(1,0,0),(1,0,1),(1,1,0)}
Encuentra la inversa de la matriz siguiente usando el método de Gauss-Jordan: aumenta la matriz con la matriz identidad y usa operaciones de fila para reducir la matriz hasta la identidad:
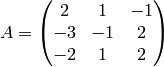
http://es.wikipedia.org/wiki/Eliminaci%C3%B3n_de_Gauss-Jordan#Encontrando_la_inversa_de_una_matriz
Usa para ello los métodos: augment , add_multiple_of_row y otros similares que encuentres entre los métodos de las matrices. Compara el resultado con la matriz inversa obtenida de forma directa.
Cuando termines, escribe código que resuelva este problema en general.
Se consideran los subespacios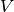 
y 
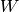del espacio vectorial real 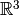. Las ecuaciones paramétricas de 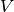son
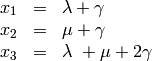
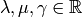
siendo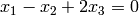 
la ecuación (implícita) de $W$. Hallar
- Bases de
y
.
- Ecuaciones (implícitas) de
- Una base de un complementario de
- Las coordenadas de
respecto de la base de
- Hallar la forma de Jordan y una matriz de paso de las siguientes matrices.
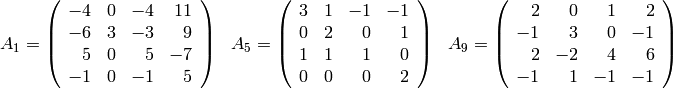
- Busca métodos para calcular el polinomio característico (characteristic polynomial) y el polinomio mínimo (minimal polynomial) de estas matrices. Factoriza ambos polinomios y comprueba que el polinomio mínimo divide al característico.
- Calcula los autoespacios asociados a cada autovalor calculando el núcleo de
. Compara el resultado con los autoespacios calculados antes.
Para cada k, definimos el polinomio de una variable:
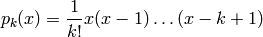
Los polinomios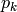 
forman una base del espacio de polinomios, al igual que los monomios 
.
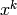- Comprueba que a pesar de tener coeficientes fraccionarios, todos los polinomios de arriba toman siempre valores enteros cuando x es un entero (es decir, tras evaluar unos cuantos de esos polinomios en unos cuantos enteros x sólo se obtienen valores enteros).
- Dado un polinomio cualquiera, expresado como una expresión simbólica en la variable x, encuentra sus coeficientes en la base formada por los
El divisor fijo de un polinomio es el máximo común divisor de los valores que toma, cuando x toma como valores todos los números enteros.
- Genera unos cuantos polinomios aleatorios con divisor fijo mayor que 1. Define el número h del polinomio como el máximo común divisor de los coeficientes de p en la base