En esta sesión vamos a trabajar con algunas funciones de Sage para trabajar con números (algunas ya las hemos usado), y a implementar algunos algoritmos clásicos de teoría de números.
Esta vez no vamos a separar la teoría de los ejercicios . En realidad, no vamos a usar funciones de Sage ni características de Sage que no hayamos visto antes. Debajo tienes varios temas de teoría de números, con una pequeña introducción y un recordatorio de algunas funciones que pueden ser útiles, y de varios ejercicios de dos grupos. El primer grupo consiste de ejercicios básicos que deberías intentar resolver en esta misma sesión. El segundo grupo consiste de ejercicios para resolver en casa . La siguiente sesión resolveremos buena parte de los ejercicios.
Aunque hemos escrito nuestra propia función para recuperar los dígitos de un número en una base B arbitraria (o casi), también podemos usar el método digits , que tienen los enteros de Sage ( Integer ).
sage: a = 17
sage: print a.digits(base=2)
sage: print a.digits(base=10)
sage: print a.digits(base=3)
[1, 0, 0, 0, 1]
[7, 1]
[2, 2, 1]
Sin embargo, no he podido encontrar la función inversa.
Escribe una función que acepta como argumentos:
- una lista de enteros (los dígitos)
- un entero (la base)
y devuelve el entero que tiene esa lista de dígitos en esa base.
Escribe una función que devuelva True si un número es divisible por 9 usando el criterio que dice: “un número es divisible por 9 si y sólo si la suma de sus dígitos es divisible por 9”. Si la suma de los dígitos es mayor que 9, puedes llamar a la función recursivamente para decidir si verifica el criterio. No debería usar el resto de la división ( % ) en ningún momento.
El método reverse invierte los elementos de una lista.
lista = [2,4,7]
lista.reverse()
print lista
> [7,4,2]
Utiliza este método y las técnicas de este capítulo para construir:
- Una función que acepta un número y te devuelve otro número, con las mismas cifras que el anterior pero en orden inverso.
- Una función que acepta un número y devuelve un booleano: True si es palíndromo (se lee igual de derecha a izquierda que de derecha a izquierda) y False si no lo es.
http://projecteuler.net/index.php?section=problems&id=36
Encuentra todos los números menores que un millón que son palíndromos tanto en base 2 como en base 10 .
Por ejemplo, 585 se escribe 1001001001 en binario. Ambas expresiones se leen igual al derecho que al revés.
- is_prime(k) : Comprueba si k es primo.
- next_prime(k) : Devuelve el menor número primo mayor que k.
- prime_range(k) : Lista de primos menores que k.
- factor(k): factorización de k. list( factor(k) ) devuelve una lista de tuplas con cada factor y su exponente correspondiente.
El teorema de Dirichlet dice que hay infinitos números primos en una sucesión del tipo:
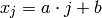
siempre que a y b sean números primos entre sí.
http://es.wikipedia.org/wiki/Teorema_de_Dirichlet
Dados tres números a, b y N, encuentra el menor número primo de la forma aj+b con j mayor que N:
El teorema del número primo afirma que el siguiente límite existe y es igual a 1:
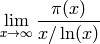
donde 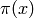 es la cantidad de números primos menores que x y ln(x) es el logaritmo neperiano.
es la cantidad de números primos menores que x y ln(x) es el logaritmo neperiano.
- Escribe un código que evalúe la función
para un número x cualquiera.
- Encuentra un número x tal que el límite diste de 1 menos de 0.1
Halla la secuencia más larga de números consecutivos menores que un millón que no contiene ningún primo.
La función 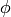 de Euler se puede calcular utilizando la factorización del número. Si
de Euler se puede calcular utilizando la factorización del número. Si 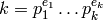 , tenemos:
, tenemos:
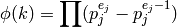
Utiliza el método factor aplicado a números enteros y la fórmula de arriba para calcular el valor de la función 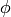 de Euler:
de Euler:
- Compara el resultado con el obtenido usando la regla “
es la cantidad de números menores que k que son primos relativos con k”, o bien con alguna función de Sage que haga la misma tarea.
El algoritmo de euclides calcula el máximo común divisor ( mcd ) de dos números naturales n y m. El algoritmo se basa en el siguiente principio: el mcd de dos números n y m, con n<m, es también el mcd de n y m%n (el resto de dividir m por n). De esta forma, hemos reducido el problema a otro con números menores. Eventualmente, uno de los dos números será 0, y entonces sabemos que mcd(0,m)=m.
Escribe una función que calcule el máximo común divisor de dos números siguiendo el algoritmo de Euclides.
Escribe una función que acepte una lista de números como argumento y devuelva el máximo común divisor de los números de la lista.
Escribe una función que calcule el máximo común divisor de dos números calculando la factorización de cada uno de ellos y después escogiendo los factores comunes con el menor exponente.
Una identidad de Bézout muestra explícitamente el mcd d de m y n como una combinación lineal de m y n con coeficientes enteros:
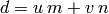
La función xgcd de SAGE implementa el algoritmo extendido de Euclides, que devuelve una tupla con el mcd y los coeficientes de una identidad de Bézout:
(d,u,v)=xgcd(m,n)
sage: m=15
sage: n=21
sage: (d,u,v)=xgcd(m,n)
sage: print '%d=(%d)*%d+(%d)*%d'%(d,u,m,v,n)
3=(3)*15+(-2)*21
También podemos encontrar una identidad del tipo
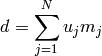
donde d es el máximo divisor común a todos los números 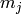 . De hecho, el proceso para encontrarlo se reduce al anterior, usando inducción. Como ya sabemos resolver el caso N=2 , sólo tenemos que aprender a reducir el caso de N+1 números al caso anterior.
. De hecho, el proceso para encontrarlo se reduce al anterior, usando inducción. Como ya sabemos resolver el caso N=2 , sólo tenemos que aprender a reducir el caso de N+1 números al caso anterior.
Para unos números 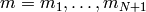 , comenzamos por encontrar una identidad de Bezout para los dos últimos:
, comenzamos por encontrar una identidad de Bezout para los dos últimos:
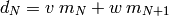
Después aplicamos la hipótesis de inducción a 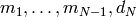 :
:
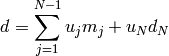
El mcd de 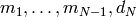 es también el de
es también el de 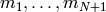 , así que sólo tenemos que sustituir:
, así que sólo tenemos que sustituir:
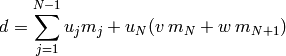
Escribe una función que acepta como argumento una lista de números 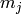 y devuelve una lista que contiene en primer lugar el máximo común divisor de todos los elementos de la lista, seguido de los ceficientes
y devuelve una lista que contiene en primer lugar el máximo común divisor de todos los elementos de la lista, seguido de los ceficientes 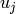 que realizan la identidad:
que realizan la identidad:
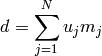
Con la identidad de Bézout podemos hacer funcionar el teorema chino del resto:
Si los números m y n son primos entre sí, entonces para cualesquiera a<m , b<n existe un único número c menor que n*m tal que el resto de dividir c entre m es a y el resto de dividir c entre n es b .
En lenguaje de congruencias, escribimos 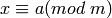 para decir que el resto de dividir a por m es el mismo que el resto de dividir x por m . El teorema chino del resto se escribe entonces:
para decir que el resto de dividir a por m es el mismo que el resto de dividir x por m . El teorema chino del resto se escribe entonces:
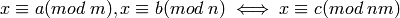
Se puede comprobar que podemos obtener c de la fórmula:
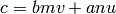
donde 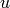 y
y  vienen de una identidad de Bézout:
vienen de una identidad de Bézout:
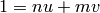
- Escribe una función que, dados a, m, b y n, devuelva c.
- Generaliza el resultado a varias congruencias
, para
, donde todos los números
son primos entre sí, y escribe una función que acepte una lista con los números
y otra con los números
y devuelva un número
tal que: