Ejercicios

1

Escribe una función recursiva que calcule la suma de los números menores o iguales que un cierto número n (es decir, 1+2+...+n). Si llamamos 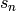a la suma de los naturales menores que 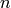, usa la regla de inducción:

2.

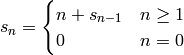
Escribe una función recursiva que calcule la suma de las cifras decimales del número que se le pasa como argumento.

Pista: si llamamos 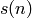a la suma de las cifras de n , usa la regla de inducción:

3.

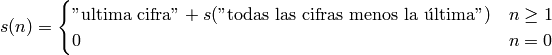
La exponenciación tiene una definición recursiva fácil de trasladar al ordenador:

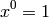
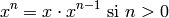
Escribe una función recursiva que calcule la potencia con un exponente entero y positivo.

4.

Usa la función reduce para escribir una función que multiplica los elementos de una lista.

5.

• Escribe una función que acepta dos argumentos, ambos listas, y devuelve una tercera lista con los elementos comunes a las dos listas que se pasaron como argumentos (es decir, la intersección).
• Usa la función reduce para escribir una función que acepta como único argumento una lista cuyos elementos son a su vez listas, y devuelve otra lista con la intersección de todas ellas.

6.

Nota : Para este ejercicio y los que siguen, intenta usar las técnicas de transformar y filtrar listas aprendidas en la hoja del bloque I sesión III.

A partir de la lista de números de abajo:

1. Consigue otra que contenga el resultado de evaluar la función
2. Consigue otra que contenga el resto de dividir cada uno de ellos por 5
3. Consigue otra que contenga, en vez de cada número, una tupla con los restos de dividir el numero por 2, 3 y 5.
4. Consigue otra que contenga, en vez de cada número, una cadena de caracteres con tantos asteriscos como indica el número.
5. Consigue otra que contenga sólo aquellos que son múltiplos de 3
6. Consigue otra que contenga sólo aquellos que son múltiplos de 3 ó de 5

sage: numeros = [1, 3, 7, 9, 11, 13, 18, 19, 21, 30, 31, 35]

7.

A partir de la lista de palabras de debajo:

1. Consigue otra que contenga las mismas palabras, pero con cada palabra seguida de puntos suspensivos
2. Consigue otra que contenga cada palabra repetida dos veces
3. Consigue otra que contenga sólo las palabras de dos letras
4. Consigue otra que contenga la primera letra de cada palabra

sage: palabras=['En', 'un', 'lugar', 'de', 'la', 'Mancha', 'de', 'cuyo', 'nombre', 'no', 'quiero', 'acordarme']

8.

Escribe código que genere una lista cuyos elementos son cadenas de caracteres:

• Dado un entero k, la lista contiene k cadenas, que dicen ‘j elefantes se balanceaban’, para cada j que va desde 1 hasta k. Por ejemplo, para k = 5:

['1 elefantes se balanceaban', '2 elefantes se balanceaban', '3 elefantes se balanceaban', '4 elefantes se balanceaban', '5 elefantes se balanceaban']

9.

• Dado un entero k, la lista contiene k cadenas, que dicen ‘j botellas contra la pared’, para cada j que disminuye desde k hasta 1. Por ejemplo, para k = 5:

['5 botellas contra la pared', '4 botellas contra la pared', '3 botellas contra la pared', '2 botellas contra la pared', '1 botellas contra la pared']

10.

Escribe código que responda a las siguientes preguntas:

• ¿Son todos los números de la lista de abajo primos?
• ¿Alguno es primo?
• Para cada número k de la lista de abajo, ¿k^2+2 es primo?
• La suma de los números de abajo, ¿es un número primo?
• ¿Cuál es el mayor número k de la lista de abajo tal que 2*k+1 es primo?

sage: numeros = [33, 39, 45, 57, 81, 99, 105, 111, 117]

11.

Ejercicio opcional (leer sólo si has seguido la sección opcional de la hoja b1s3).

Para generar los números de Fibonacci, tendríamos que escribir algo así como:

g = (fibonacci(k) for k in range(K))

Como el cálculo del k-ésimo número de Fibonacci requiere más cálculos cuanto mayor es k (dependiendo de cómo hagamos los cálculos), esta opción es poco eficiente.

Escribe un generador (de más de una línea) que devuelva los números de Fibonacci de uno en uno, pero aprovechando los cálculos realizados para calcular el número anterior.