Control del flujo del programa

Alternativas y bucles

Alternativas lógicas

La sintaxis de los bloques if..elif..else en python:

if condicion1:
    bloque de instrucciones 1
elif condicion2:
    bloque de instrucciones 2
...
else:
    bloque de instrucciones final

es bastante diferente de la otros lenguajes como C, pero la esencia es la misma: Si la primera condición es cierta, se ejecuta el primer bloque de instrucciones y se abandona el bloque de instrucciones. Si es falsa, el primer bloque de instrucciones no se ejecuta , y se pasa a evaluar la segunda condición. Si es cierta, se ejecuta el segundo bloque de instrucciones y se abandona el bloque if...else . Finalmente, si todas las condiciones son falsas, se ejecuta el bloque de instrucciones final, que va precedido de la palabra clave else .

La indentación marca el principio y el final de cada bloque . Es decir, las líneas de los bloques de instrucciones comienzan con cuatro espacios. Después del bloque if...else, el programa puede tener más líneas, que no estarán indentadas.

Al final de cada condición if, elif o else, escribimos dos puntos ( : ).

Tanto las instrucciones elif como la instrucción else son opcionales.

sage: numero = 6
sage: if numero%2==0:
...       print '%d es par'%numero
6 es par

sage: numero = 6
sage: if numero%2==0:
...       print '%d es par'%numero
sage: else:
...       print '%d es impar'%numero
6 es par

Observa en este ejemplo el papel de la indentación para marcar el principio y final de cada bloque:

sage: numero=-10
sage: if numero>0:
...       print 'La raiz de %f es %f'%(numero,numero^0.5)
sage: else:
...       print 'La raiz de %f es %f*i'%(numero,(-numero)^0.5)
sage: print 'El cuadrado de %f es %f'%(numero, numero^2)    #Esta instrucción no forma parte del bloque else
La raiz de -10.000000 es 3.162278*i
El cuadrado de -10.000000 es 100.000000

La condición puede ser cualquier expresión que al evaluar devuelva un booleano, y no se pueden hacer asignaciones . También se puede poner un número como condición (de cualquier tipo de datos), en cuyo caso 0 se interpreta como False , y cualquier otra cosa como True, o un contenedor (lista, tupla, cadena...), en cuyo caso un contenedor vacío se interpreta como False , y cualquier otra cosa como True.

sage: ls = ['a']
sage: #ls = []
sage: if ls:
...       print 'la lista no está vacía'
la lista no está vacía

Bucle for

Utilizando la instrucción for podemos repetir una misma instrucción sobre cada elemento de una lista.

for elemento in lista:
    instrucciones

El bloque de instrucciones se ejecutará una vez por cada elemento de la lista. La variable elemento tomará sucesivamente el valor de cada elemento de la lista. A cada ejecución del bloque de instrucciones lo llamamos una iteración . Veamos algunos ejemplos:

sage: suma = 0
sage: numeros = [1, 1, 3, 7, 13, 21, 31, 43]
sage: for k in numeros:
...       suma = suma + k
sage: print suma
120

sage: lista_frutas = ['pera','manzana','naranja']
sage: print '¿Por qué letra empieza cada fruta?'
sage: for palabra in lista_frutas:
...       primera_letra = palabra[0]
...       print '%s empieza por %s'%(palabra, primera_letra)
sage: print '¡eso es todo! gracias por su atención'
¿Por qué letra empieza cada fruta?
pera empieza por p
manzana empieza por m
naranja empieza por n
¡eso es todo! gracias por su atención

Bucles while

Un bucle while repite un bloque de instrucciones mientras se satisfaga una condición.

while condicion:
    instrucciones

En el ejemplo de debajo, la variable i vale 0 antes de entrar en el bucle while. Después, el valor de i aumenta en una unidad en cada iteración del bucle. Al cabo de 10 iteraciones, el valor de i es 10, y se abandona el bucle porque la condición i < 10 ya no se verifica.

sage: i = 0
sage: while i<10:
...       i = i + 1
sage: print i
10

Si accidentalmente escribes un bucle infinito o simplemente quieres detener el cálculo antes de que termine, puedes usar la acción interrupt , que está en el menú desplegable Action , al principio de la hoja de trabajo. Observa cómo al evaluar el código de abajo, aparece una línea verde debajo y a la izquierda del bloque de código. Esta línea indica que se está ejecutando el código, y que todavía no ha concluído. Al ejecutar interrupt , el cómputo se cancela, y la línea verde desaparece.

sage: x=0 #El valor de x no cambia al iterar
sage: while x<100:
...       x = x*1.5
sage: print x
^CTraceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_11.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("eD0wICNFbCB2YWxvciBkZSB4IG5vIGNhbWJpYSBhbCBpdGVyYXIKd2hpbGUgeDwxMDA6CiAgICB4ID0geCoxLjUKcHJpbnQgeA=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))' + '\n', '', 'single')
  File "", line 1, in <module>

  File "/tmp/tmp0Fuz2Y/___code___.py", line 5, in <module>
    x = x*_sage_const_1p5
  File "/home/sageadm/sage-4.4.1-linux-64bit-ubuntu_9.10-x86_64-Linux/local/lib/python2.6/site-packages/sage/interfaces/get_sigs.py", line 9, in my_sigint
    raise KeyboardInterrupt
KeyboardInterrupt
__SAGE__

Bloques anidados

Podemos anidar bloques if...else, for y while de cualquier forma posible, cuidando de que la indentación marque el principio y el final de cada bloque.

Por ejemplo, calculamos la suma de los inversos de los primos menores que k, usando un acumulador:

sage: k=100
sage: suma = 0
sage: for j in range(k):
...       if is_prime(j):
...           suma += 1/j
sage: print 'La suma de los inversos de los primos menores que %d es %.3f'%(k, suma)
La suma de los inversos de los primos menores que 100 es 1.803

En el siguiente ejemplo, tenemos dos bloques for, uno dentro de otro. Observamos que nada impide que el bucle interior haga un número distinto de iteraciones cada vez.

sage: for j in srange(10):
...       for k in srange(j):
...           print k,
...       print
0
0 1
0 1 2
0 1 2 3
0 1 2 3 4
0 1 2 3 4 5
0 1 2 3 4 5 6
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7 8

Tablas de verdad

Para obtener la tabla de verdad de una fórmula lógica, evaluamos la fórmula en cada posible combinación de valores para p, q y r. Por ejemplo, la tabla de verdad de la fórmula:

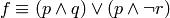
es:

p=True, q=True, r=True => f=True
p=True, q=True, r=False => f=True
p=True, q=False, r=True => f=False
p=True, q=False, r=False => f=True
p=False, q=True, r=True => f=False
p=False, q=True, r=False => f=False
p=False, q=False, r=True => f=False
p=False, q=False, r=False => f=False

Ejemplo : genera todas las combinaciones de valores para p, q y r anidando tres bucles for .

sage: for p in [True, False]:
...       for q in [True, False]:
...           for r in [True, False]:
...               #Utilizamos el codigo %s para valores booleanos,
...               #el mismo que usamos para cadenas de caracteres
...               f = (p and q) or (p and not r)
...               print 'p=%s, q=%s, r=%s => f=%s'%(p,q,r,f)
p=True, q=True, r=True => f=True
p=True, q=True, r=False => f=True
p=True, q=False, r=True => f=False
p=True, q=False, r=False => f=True
p=False, q=True, r=True => f=False
p=False, q=True, r=False => f=False
p=False, q=False, r=True => f=False
p=False, q=False, r=False => f=False

Buscar un número con ciertas propiedades

En el siguiente ejemplo, buscamos un número N primo relativo a un número k dado y tal que 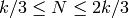. Cualquier número con esa propiedad nos vale. Podemos empezar por k/3 y seguir hacia delante, o generar números aleatorios. Esta técnica es bastante general y se puede usar en problemas de los que sabemos poco. Sin embargo, podría llevar mucho tiempo a la computadora si los números que buscamos son raros o, peor, si no hay ninguno.

En primer lugar, usamos un bucle for para iterar sobre todos los posibles casos, pero salimos del bucle usando la instrucción break cuando encontramos un número que satisface la condición.

sage: #Buscamos un numero que sea primo relativo a k
sage: #y que esté entre k/3 y 2*k/3
sage: k=196
sage: tercio = ceil(k/3)
sage: dostercios = floor(2*k/3)
sage: for x in range(tercio, dostercios):
...       if gcd(x, k) == 1:           #Si x es primo relativo a k,
...                                    #salimos del bucle for
...           break                    #gcd es el maximo comun divisor
sage: print x
67

A continuación, resolvemos el mismo problema probando con números aleatorios.

sage: #Buscamos un numero que sea primo relativo a k y que esté entre k/3 y 2*k/3
sage: #Ahora usamos numeros aleatorios
sage: k=169
sage: tercio = ceil(k/3)
sage: dostercios = floor(2*k/3)
sage: #randint(tercio, dostercios) devuelve un numero aleatorio
sage: # entre tercio y dostercios
sage: x=randint(tercio, dostercios)
sage: while gcd(x, k) != 1:
...       x = randint(tercio, dostercios)
sage: print x
110

Definición de funciones

Hemos usado ya unas cuantas funciones definidas en Sage. Ahora aprenderemos a definir nuestras propias funciones. La sintaxis para definir una función en python es:

def funcion(argumento1, argumento2, ...):
    instrucciones

De nuevo, las instrucciones que componen el cuerpo de la función están indentadas (comienzan con cuatro espacios), y la primera línea sin indentar marca el final de la declaración de la función.

Por ejemplo, una función que acepta un número como argumento, y escribe por pantalla alguna información sobre el número.

sage: def informacion(numero):
...       print 'Información sobre %d'%numero
...       if is_prime(numero):
...           print '    es primo'
...       if numero%2==0:
...           print '    es par'
...       if is_power_of_two(numero):
...           print '    es potencia de dos'

Para llamar a la función, escribimos su nombre con los argumentos entre paréntesis.

sage: informacion(2)
Información sobre 2
    es primo
    es par
    es potencia de dos

Las funciones tienen la posibilidad de devolver un valor , usando la palabra clave return . El valor devuelto por la función puede ser almacenado en una variable, o usado para hacer cálculos, exactamente igual que para las funciones definidas en Sage.

sage: def radio(x,y):
...       return sqrt(x^2 + y^2)

sage: print radio(1,2)
sqrt(5)

sage: r1 = radio(1,1)
sage: r2 = radio(5,0)
sage: print r2-r1
-sqrt(2) + 5

Observa que cuando se ejecuta una instrucción return, se devuelve el valor correspondiente, y no se ejecuta ninguna otra instrucción de la función . Observa la siguiente variante de nuestra primera función.

sage: def informacion_bis(numero):
...       if is_prime(numero):
...           return '%d es primo'%numero
...       if numero%2==0:
...           return '%d es par'%numero
...       if is_power_of_two(numero):
...           return '%d es potencia de dos'%numero

sage: info = informacion_bis(2)
sage: print info
2 es primo

Sin embargo, no podemos recoger el valor de una llamada a informacion :

sage: info = informacion(2)
sage: print info
Información sobre 2
    es primo
    es par
    es potencia de dos
None

Documentación

Es una buena práctica documentar el código. Unas semanas después de escribir el código, no es tan fácil recordar qué hacía. Aparte de escribir comentarios cuando lo creas conveniente comenzando con el carácter # , las declaraciones de funciones tienen una descripción ( docstring ), que muchos programas utilizan para mostrar información de la función en momentos apropiados. El lugar donde colocar la doctring es justo debajo de la definición de la función, y también indentado respecto de la función. La docstring es sólo una cadena de caracteres , y por tanto se puede separar entre comillas simples (‘cadena’), comillas dobles (“cadena”), o triples comillas simples para cadenas más largas (‘’‘cadena larga’‘’).

def funcion(argumento1, argumento2, ...):
    '''docstring
    '''
    instrucciones

Vamos a definir de nuevo las dos funciones anteriores colocando en su sitio las docstring de las funciones.

sage: def informacion(numero):
...       '''Imprime en pantalla alguna informacion sobre un numero
...
...       Imprime una linea que dice si es primo, otra que dice si
...       es par...
...       '''
...       print 'Información sobre %d'%numero
...       if is_prime(numero):
...           print '    es primo'
...       if numero%2==0:
...           print '    es par'
...
...       #is_power_of_two devuelve True si el numero es
...       #potencia de dos
...       if is_power_of_two(numero):
...           print '    es potencia de dos'
...
sage: def radio(x,y):
...       '''Devuelve la coordenada radial del punto con coordenadas cartesianas dadas
...
...       Tiene dos argumentos
...       '''
...       return (x^2 + y^2)^.5

Una manera inmediata de acceder a las docstring de todas las funciones, incluso si no las hemos definido nosotras, es escribir en un cuadro de código el nombre de la función seguido de una interrogación.

sage: informacion?
<html>...</html>

sage: radio?
<html>...</html>

sage: sin?
<html>...</html>

sage: is_prime?
<html>...</html>

sage: factorial?
<html>...</html>

¿Cuándo usar una función?

Como regla general, siempre que, resolviendo un problema, podamos identificar una subtarea claramente delimitada, debemos escribirla como función. Una tarea está bien delimitada cuando podemos describir a otra persona cuáles son los datos de entrada (un número entero, dos números reales, una cadena de caracteres y dos números naturales ...), cuáles son los datos de salida, y qué tiene que hacer la función, sin necesidad de explicarle cómo lo hemos hecho.

Veamos un ejemplo. Escribimos antes un código que calculaba la suma de los inversos de los primos menores que k. Identificamos una tarea bien delimitada: una función que recibe un número k y devuelve la suma de los inversos de los primos que son menores que k. Escribimos ahora una función que realiza esta tarea usando el código de la sesión anterior: nos limitamos a copiar el código que usamos antes, y lo colocamos dentro del cuerpo de una función.

sage: def sumaprimos(k):
...       '''Suma los inversos de los primos menores que un numero dado
...       '''
...       suma = 0
...       for j in srange(k):
...           if is_prime(j):
...               suma = suma + 1/j
...       return suma

sage: print 'La suma de los inversos de los primos menores que 100 es %f'%sumaprimos(100)
La suma de los inversos de los primos menores que 100 es 1.802817

Al conjunto formado por el nombre de la funcion, la descripción de los datos de entrada y la descripción de los datos de salida, se le llama la signatura de la función. Al código concreto que hemos escrito para realizar la tarea, se le llama la implementación . Distintas implementaciones de la misma tarea pueden conseguir el mismo resultado. Si no se cambia la signatura, es posible cambiar la implementación de la función sin necesidad de cambiar el código que usa la función.

Nos damos cuenta ahora de que hay una función, prime_range , que devuelve directamente una lista de números primos. Podemos utilizar esta función para mejorar la implementación de sumaprimos .

sage: prime_range?
<html>...</html>

sage: def sumaprimos(k):
...       '''Suma los inversos de los primos menores que un numero dado
...
...       Esta version de sumaprimos usa prime_range
...       '''
...       suma = 0
...       for j in prime_range(k):
...           suma = suma + 1/j
...       return suma

Aunque hemos cambiado la implementación, la signatura es la misma, y podemos llamar a sumaprimos de la misma forma que antes.

sage: print 'La suma de los primos menores que 100 es %f'%sumaprimos(100)
La suma de los primos menores que 100 es 1.802817

Tratar con argumentos erróneos

El lenguaje python tiene una forma muy sofisticada de tratar con los errores en tiempo de ejecución. Si algún fragmento de código produce un error, lanza una excepción . Por ejemplo, si una función espera datos de cierto tipo y recibe datos de otro tipo distinto, lanza un TypeError , o si realiza una división por cero lanza un ZeroDivisionError .

sage: range('a')
Traceback (most recent call last):
...
TypeError: range() integer end argument expected, got str.

sage: def funcion(a):
...       return 1/a

sage: funcion(0)
Traceback (most recent call last):
...
ZeroDivisionError: Rational division by zero

Los errores se propagan desde la línea que produjo el error a través de la pila de ejecución.

sage: def otra_funcion(a,b):
...       return a + funcion(b)

sage: otra_funcion(1,0)
Traceback (most recent call last):
...
ZeroDivisionError: Rational division by zero

Es importante leer las descripciones de los errores por si nos dan una pista de cuál puede ser el problema con una función que no arroja un error.

Aunque no profundizaremos en el sistema de excepciones de python, si en algún momento sentimos la necesidad de asegurarnos de que los datos de entrada de nuestras funciones verifican ciertas restricciones, utilizaremos la sintaxis ” raise Exception ”.

Por ejemplo, si en la siguiente implementación de la función factorial recibimos un número negativo corremos el riesgo de entrar en un bucle infinito:

sage: def factorial(n):
...       acumulador = 1
...       k = n
...       while k!=0:
...           acumulador *= k
...           k -= 1
...       return acumulador

Para evitar esto, comprobamos que el número sea positivo y, de otro modo, lanzamos una excepción genérica junto con un mensaje de error:

sage: def factorial(n):
...       if n <= 0:
...           raise Exception, 'El argumento de factorial debe ser positivo'
...       acumulador = 1
...       k = n
...       while k!=0:
...           acumulador *= k
...           k -= 1
...       return acumulador

sage: factorial(-3)
Traceback (most recent call last):
...
Exception: El argumento de factorial debe ser positivo