Las superficies producto son una notable aportación al diseño, pero existen otros procedimientos para generar superficies, algunos de ellos anteriores a la aparición de las NURBS. Estos formalismos alternativos están basados en curvas, lo cual es la situación habitual en la industria. Lo usual es trazar varias secciones del objeto, un avión, un buque..., según planos longitudinales y transversales, de modo que quede acotado por una malla de curvas en el espacio. Sólo resta, por tanto, interpolar sobre dicha malla para definir una superficie admisible del objeto, dentro de unas tolerancias de curvatura, dimensiones, volumen...
Nuestro objetivo, pues, es describir maneras sencillas de rellenar con una superficie el espacio entre dos, tres o cuatro curvas, lo cual se logra, entre otros métodos, con superficies regladas, traslacionales y de Coons. Trataremos en lo posible de relacionar estos esquemas con nuestro formalismo.
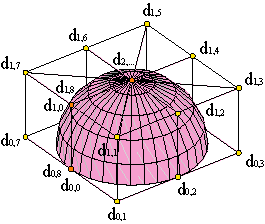
Otras superficies generadas a partir de curvas son las superficies de revolución, las cuales, por su simetría, que comparten con numerosas piezas y partes de los objetos de la industria, son especialmente relevantes en el diseño. Les dedicaremos, pues, un apartado en este tema.
Aparte, en algunas industrias basadas principalmente en el acero, como es la naval, es característico el uso de planchas que no se pueden deformar, lo cual implicaría fundición, sino tan sólo doblar o enrollar, es decir, manipulaciones que no supongan la aparición de curvatura en la plancha. Así pues, es fundamental el diseño, en lo posible, por superficies de curvatura nula, llamadas desarrollables, o que se les aproximen dentro de una tolerancia.
Vídeo de Superficies traslacionales
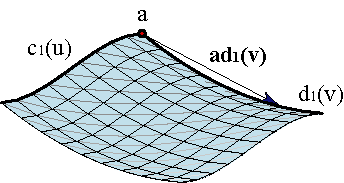
Las superficies traslacionales son la solución más sencilla a un problema de determinación de superficies: supongamos que tenemos dos curvas parametrizadas, c1(u), d1(v), u,v∊[0,1], que se cortan en el punto inicial, c1(0) = a = d1(0). Queremos hallar una superficie parametrizada c(u,v) que pase por ambas curvas, de modo que c(0,v) = d1(v), c(u,0) = c1(u).
Obviamente, hay infinitas superficies que son solución de este problema, pero la más sencilla consiste en deslizar la curva c1(u) paralelamente a sí misma a lo largo de la curva d1(v). Ejemplo. Esto se consigue trasladando el punto c1(u) por el vector ad1(v), es decir,
| (1) |

Nótese que estas superficies están caracterizadas por la condición de twist nulo,
| (2) |
Estas superficies se denominan superficies traslacionales.
No es difícil encajar este tipo de superficies en nuestro formalismo y construir, por tanto, superficies traslacionales de Bézier, racionales o spline. Para ello, sólo es preciso contar con dos curvas que posean dichas características.
Supongamos que c1(u), d1(v) son curvas de Bézier de grados m y n y polígonos de control {c10,...,c1m}, {d10,...,d1n}, respectivamente. El punto de corte es c10 = a = d10. Como la superficie traslacional c(u,v) pasa por ambas curvas, estos vértices nos proporcionan una columna y una fila del borde de la malla de control. Ejemplo. El resto de vértices se infieren de la condición de twist nulo. Ejemplo. En nuestro caso,
| (3) |
Esta relación es también válida para superficies B-spline. Para superficies racionales o B-spline racionales, hay que añadir la relación para los pesos,
| (4) |
Vídeo de Superficies regladas y de Coons
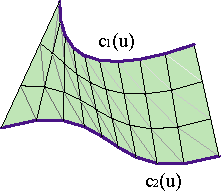
Supongamos que tenemos dos curvas parametrizadas, c1(u), c2(u), en el mismo intervalo u∊[0,1] y queremos construir una superficie, c(u,v), cuyo borde contenga a ambas,
| (5) |
Una solución consiste en enlazar cada punto de la primera curva, c1(u0), con aquel de la segunda que le corresponde por su valor del parámetro u, c2(u0) por medio de una recta. Son las superficies regladas. Ejemplo. La parametrización de la superficie reglada es
| (6) |
Construir superficies regladas de Bézier no es ningún problema, ya que si c1(u), c2(u) son curvas de grado m y polígonos de control {c10,..., c1m}, {c20,...,c2m}, la superficie reglada necesariamente será de grado (m,1), con lo cual su malla de control está formada por los polígonos de ambas curvas, {c10,c20,..., c1m,c2m}. Ejemplo.
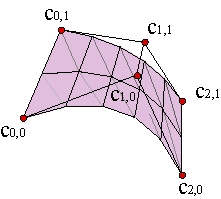
Este resultado es válido asimismo para superficies regladas B-spline. Para superficies racionales o B-spline racionales, sólo es preciso añadir la matriz de pesos que, de acuerdo con el razonamiento anterior, está formada por los pesos de las dos curvas, {w10,w20,..., w1m,w2m}.
Un caso particular de superficies regladas son las superficies desarrollables. Geométricamente se caracterizan por tener curvatura gaussiana nula, lo cual quiere decir que son intrínsicamente planas. Son planos o regiones planas que se sumergen en el espacio sin deformarse. Por ello se pueden extender sobre el plano, de ahí el nombre de superficies desarrollables.
Consideremos una superficie desarrollable parametrizada por c(u,v). Si n(u,v) es un vector normal a la superficie en el punto c(u,v), la condición de curvatura nula se expresa como
| (7) |
La condición (7) se puede desgranar aún más. Una superficie reglada es desarrollable si y sólo si para todo par de puntos homólogos, los generadores de las curvas y de la recta que los une están en un mismo plano.
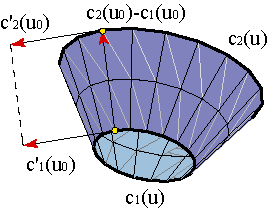
Ejemplos sencillos de superficies desarrollables, aparte del propio plano, son las superficies cilíndricas y cónicas.
Las superficies cilíndricas son las superficies regladas, o partes de ellas, en las que la curvas c1(u), c2(u) se obtienen una a partir de otra por medio de una traslación,
| (8) |
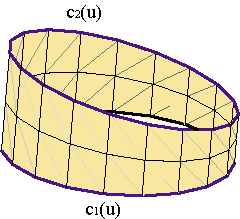
Las superficies cilíndricas se pueden interpretar como superficies traslacionales en las que la segunda curva es una recta, d1(v) = a + v v. O, con mayor generalidad, las superficies cilíndricas son superficies regladas en las cuales todas las rectas generatrices son paralelas.
Las superficies cónicas se generan mediante el haz de rectas que une cada punto de una curva c1(u) con un punto fijo a, el vértice del cono,
| (9) |
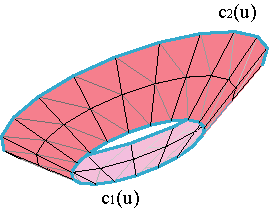
No es sencillo caracterizar las superficies desarrollables de grado (1,n) en términos de su malla de control.
Vídeo de Superficies regladas y de Coons
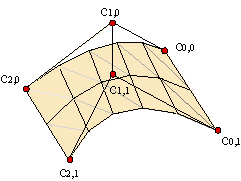
Supongamos que tenemos cuatro curvas parametrizadas, c1(u), c2(u), d1(v), d2(v), u,v∊[0,1], que forman un cuadrilátero curvo, es decir,
| ||||||||||||||
| ||||||||||||||
Existen infinitas superficies que satisfacen estas condiciones, por lo que nos limitaremos a proporcionar una de las más sencillas.
Denotaremos por cc(u,v) la superficie reglada que se apoya en c1(u) y c2(u) y por cd(u,v), la que se apoya en d1(v) y d2(v),
| |||||
Si a la suma de las parametrizaciones regladas cc(u,v) y cd(u,v) le restamos otra reglada, un paraboloide hiperbólico, que interpole entre los bordes espúreos,
| ||||||||||||||
| (14) |
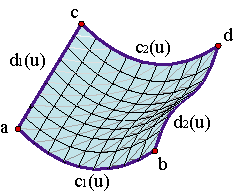
Estas superficies se denominan superficies de Coons y generalizan e incluyen las superficies regladas. Ejemplo.
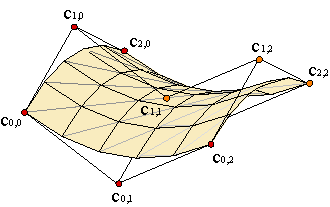
Después de haber estudiado las superficies regladas, no es difícil describir las superficies polinómicas de Coons. Supongamos que c1(u), c2(u) son curvas de grado m y polígonos de control {c10,..., c1m}, {c20,..., c2m}, respectivamente. A su vez, d1(v), d2(v) son curvas de grado n y polígonos {d10,..., d1n}, {d20,...,d2n}. Para obtener la malla de la superficie de Coons, tendremos que elevar el grado de todas ellas hasta (m,n). Ejemplo. Así pues, los vértices de la malla de control de la superficie de Coons, {c0,0,..., cm,n}, se podrán expresar como
| (15) |
| |||||||||||||||||||||||||||||||||||||||
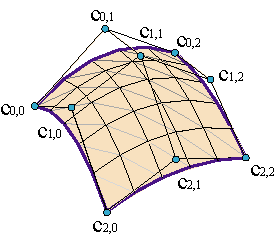
De igual modo podemos construir superficies de Coons B-spline, usando el algoritmo de inserción para que las tres superficies auxiliares tengan los mismos nudos. Primero elevaríamos el grado de las tres parametrizaciones hasta que todas alcancen el grado (m,n) y luego insertaríamos los nudos no comunes para que todas tengan las mismas sucesiones de nudos.
Las superficies de Coons racionales tampoco presentan especial problema, ya que hemos estudiado ya como construir superficies regladas a partir de curvas racionales. Sin embargo, no es trivial construir mallas de control y pesos para ellas.

Las superficies de Coons se pueden emplear para interpolar una malla de curvas en el espacio, de modo que cada cuadrilátero curvo defina una superficie de Coons. Consideremos una única superficie de Coons. Si la queremos enlazar con otra superficie, por ejemplo, a lo largo de la curva correspondiente a u = 1, d2(v), tenemos que la derivada transversal a lo largo de dicho borde es
| ||||||||||||||||
Por tanto, observamos un efecto no deseado. El valor de la derivada transversal en u = 1 depende de los valores en u = 0, es decir, de la curva opuesta del borde, d1(v), lo cual complica sobremanera el engarce diferenciable con una segunda superficie. Ejemplo.
Una solución sería utilizar los polinomios cúbicos B30(u)+B31(u) y B32(u)+B33(u) como funciones de interpolación o directamente utilizar los polinomios de Bernstein de grado tres.
Vídeo de Superficies de revolución
Como es bien sabido, las superficies de revolución se generan por rotación de una curva plana en torno a un eje contenido en dicho plano. Ejemplo. Por ejemplo, si la curva está contenida en el plano XZ, c1(u) = (f(u),0,g(u)), una parametrización de la correspondiente superficie de revolución obtenida al girar en torno al eje Z es
| (18) |
Las líneas de parámetro v constante, copias rotadas de la curva original, son los meridianos de la superficie. Las líneas de u constante, circunferencias descritas al girar los puntos de la curva, son los paralelos de la superficie, de radio ¦f(u)¦.
En el Ejemplo vemos cómo se construye el polígono B-spline de circunferencias con N tramos.
Por tanto, para construir la malla de control de una superficie de revolución generada por una curva plana racional de polígono {c0,..., cn} y pesos {w0,...,wn}, sólo es preciso ir rotando el polígono hasta cada una de las posiciones de los vértices de la circunferencia, multiplicando por un medio 21/2/2 en el caso de cuatro arcos) los pesos de los vértices intermedios, los que no están sobre la circunferencia. Así los meridianos estarán descritos por columnas de la malla y los paralelos, por sus filas. Ejemplo.
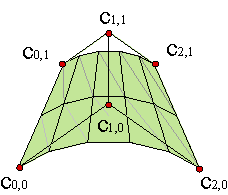
La construcción anterior también es válida para curvas B-spline, ya que la descripción que hemos hecho de los arcos de circunferencia es el propio polígono B-spline para un único tramo, sin más que incluir los nudos triviales, {0,0,1,1}.
El proceso es esencialmente el mismo. Se traslada el polígono anterior a cada punto del polígono B-spline de la curva que se va a rotar, modificando los radios y las alturas, y se multiplican los pesos, como se hacía para superficies de Bézier de revolución.