1 Introducción

Vídeo de Superficies

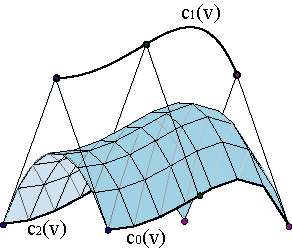
El diseño de superficies debería ser, en principio, más complejo que el diseño de curvas que hemos estudiado hasta el momento. Sin embargo, muchas de las herramientas y algoritmos que hemos desarrollado para las curvas nos van a seguir siendo útiles para las superficies, lo cual no quita para que estas posean sus especificidades.

Pensemos por ejemplo en una curva polinómica espacial de polígono de control {c₀,..., c_m}, c_i ∊ A³. Su representación nos es ya conocida,

c(u) = Σ_{i = 0}^m c_i B^m_i(u) .

Si permitimos que los vértices del polígono de control se muevan a su vez a lo largo de curvas parametrizadas, c_i(v),

c(u,v) = Σ_{i = 0}^m c_i(v) B^m_i(u) ,

las curvas de Bézier c(u,v₀), de polígonos {c₀(v₀),..., c_m(v₀)}, evolucionan en el espacio describiendo una superficie parametrizada c(u,v). Ejemplo. . fig501

2 Superficies de Bézier

Vídeo de Superficies de Bézier

No nos va a interesar que los vértices evolucionen a lo largo de curvas arbitrarias c_i(v), sino según curvas de Bézier de grado n, con polígonos de control respectivos {c_i,0,...,c_i,n}. De este modo, la parametrización de la superficie resultante,

c(u,v) = Σ_{i = 0}^mΣ_{j = 0}ⁿc_i,jB^m_i(u)Bⁿ_j(v) , u,v ∊ [0,1] ,

(1)

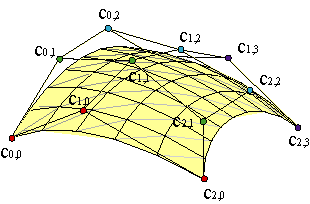
será una superficie de bigrado (m,n) y estará descrita por una malla de control de (m+1)(n+1) vértices, {c_0,0,...,c_m,n}. Ejemplo. fig500

Las curvas de parámetro u constante,

c(u₀,v) = Σ_{j = 0}ⁿ(Σ_{i = 0}^mc_i,jB^m_i(u₀))Bⁿ_j(v) , v ∊ [0,1] ,

son curvas de Bézier de grado n y polígono de vértices c_j = (Σ_ic_i,jB^m_i(u₀)). Mientras que las curvas de parámetro v constante,

c(u,v₀) = Σ_{i = 0}^m(Σ_{j = 0}ⁿc_i,jBⁿ_j(v₀))B^m_i(u) , u ∊ [0,1] ,

son curvas de grado m y vértices c_i = (Σ_jc_i,jBⁿ_j(v₀)). Ejemplo.

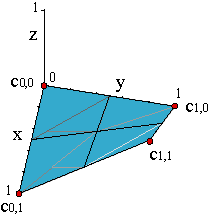
Al igual que sucedía con las curvas no paramétricas, nuestro formalismo permite representar gráficas de funciones polinómicas de dos variables, f(u,v), ya que las podemos parametrizar como c(u,v) = (u,v,f(u,v)). Ejemplo. Si expresamos f(x,y) como combinación de una malla de control sobre la recta real, { c'_0,0,..., c'_m,n}, la gráfica de la función estará determinada por su malla de control { c_0,0,..., c_m,n}, cuyos vértices son

c_i,j = (

, c'_i,j) .

(2)

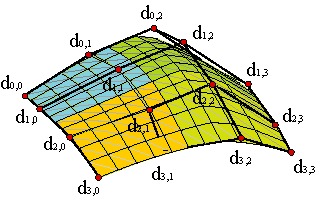
La representación producto se adapta asimismo para construir superficies B-spline. Sólo hay que sustituir los polinomios de Bernstein por las funciones B-spline. Así pues, para determinar una superficie B-spline de bigrado (m,n) y MxN tramos, será preciso indicar dos sucesiones de nudos, {u₀,..., u_2m+M-2}, {v₀,..., u_2n+N-2} y una malla de control formada por los vértices {d_0,0,...,d_m+M-1,n+N-1}. La parametrización,

c(u,v) = Σ_{i = 0}^m+M-1Σ_{j = 0}^n+N-1d_i,jN^m_i(u)Nⁿ_j(v) ,

(3)

está definida en el recinto [u_m-1,u_m+M-1]x[v_n-1,v_n+N-1]. fig504

Al igual que sucedía con las curvas B-spline, lo más común es que las sucesiones comiencen y acaben con m y n nudos repetidos. Ejemplo

Tampoco causa mayor trastorno la inclusión de pesos, {w_i,j}, para obtener superficies racionales y racionales a trozos,

c(u,v) =

Σ_{i = 0}^mΣ_{j = 0}ⁿw_i,jc_i,jB^m_i(u)Bⁿ_j(v) ,

Σ_{i = 0}^mΣ_{j = 0}ⁿw_i,jB^m_i(u)Bⁿ_j(v) ,

(4)

que nos permiten representar de manera exacta un cilindro, por ejemplo.

c(u,v) =

Σ_{i = 0}^m+M-1Σ_{j = 0}^n+N-1w_i,jd_i,jN^m_i(u)Nⁿ_j(v) ,

Σ_{i = 0}^m+M-1Σ_{j = 0}^n+N-1w_i,jN^m_i(u)Nⁿ_j(v) .

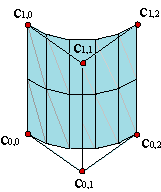
(5)

3 Propiedades de las superficies de Bézier

Como las superficies de Bézier son una generalización natural de las curvas polinómicas, muchas de las propiedades de estas se mantienen. En particular, como

Σ_{i = 0}^mΣ_{j = 0}ⁿB^m_i(u)Bⁿ_j(v) = 1 ,

(6)

nuestra base de funciones es también partición de la unidad.

Este hecho traía consigo numerosas buenas propiedades, como la invariancia afín de la parametrización,

f(c(u,v)) = Σ_{i = 0}^mΣ_{j = 0}ⁿf(c_i,j)B^m_i(u)Bⁿ_j(v) , u,v ∊ [0,1] ,

(7)

para cualquier aplicación afín f. Aparte, las superficies racionales mantienen la invariancia proyectiva.

La superficie sigue estando comprendida, si los pesos son todos positivos, en la envolvente convexa de la malla de control. Ejemplo. En el caso de superficies a trozos, cada tramo de superficie está además comprendido en la envolvente convexa de su malla de control.

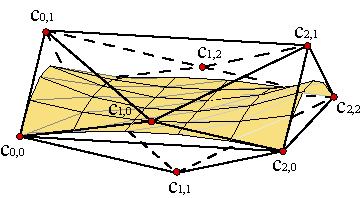
Sin embargo, no hay una generalización sencilla de la propiedad de disminución de la variación. Es fácil, por ejemplo, comprobar que una recta puede cortar a la superficie en más puntos que los que corta al poliedro descrito por la malla de control.

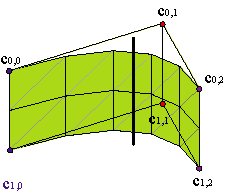
Por supuesto, si queremos definir la parametrización en un recinto rectangular, [a,b]x[c,d] distinto del que hemos empleado hasta el momento, [0,1]x[0,1], no precisamos más que realizar una reparametrización afín de los parámetros u,v, que no afecta ni a la malla de control ni a la gráfica de la superficie,

u( u' ) =

u'-a

b-a

, u' ∊ [a,b] , v( v' ) =

v'-c

d-c

, v' ∊ [c,d] ,

de modo que la nueva parametrización sea

c'(u', v') = c(u( u ),v(v')): = c(

u'-a

b-a

v'-c

d-c

) , u' ∊ [a,b] , v' ∊ [c,d] .

Del mismo modo que las curvas de Bézier sólo pasan por los vértices extremos, correspondientes a t = 0, t = 1, las superficies sólo pasan por cuatro vértices, las esquinas de la malla de control,

c_0,0 = c(0,0) , c_m,0 = c(1,0) , c_0,n = c(0,1) , c_m,n = c(1,1) ,

aunque la superficie pasa por las cuatro curvas de Bézier que describen los bordes de la malla de control. Ejemplo. Por ejemplo, para u = 0,

c(0,v) = Σ_{j = 0}ⁿc_0,jBⁿ_j(v) , v ∊ [0,1] ,

la curva correspondiente, c(0,v), tiene por polígono de control {c_0,0,..., c_0,n}, la primera fila de la malla de control de la superficie. Del mismo modo, la última fila, {c_m,0,..., c_m,n}, es el polígono de control de la curva c(1,v). Y, para v = 0,

c(u,0) = Σ_{i = 0}^mΣ_{j = 0}ⁿc_i,jB^m_i(u)Bⁿ_j(0) = Σ_{i = 0}^mc_i,0B^m_i(u) , u ∊ [0,1] ,

el polígono de control de la curva c(u,0) es la primera columna de la malla de control, {c_0,0,..., c_m,0}. De manera análoga, el polígono de control de c(u,1) es la última columna, {c_0,n,..., c_m,n}.

Por tanto, el borde de la malla se corresponde con el borde de la superficie. Ejemplo.

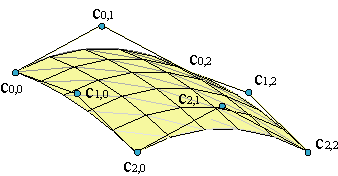
Esta propiedad se mantiene en las superficies racionales y en las superficies a trozos, si el nudo del comienzo y del final de cada sucesión tiene la multiplicidad igual al grado.

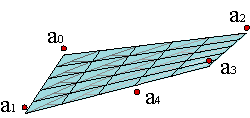
Las superficies a trozos siguen poseyendo la propiedad de control local. Un vértice genérico de la malla de control afecta a lo sumo a (m+1)·(n+1) tramos de la superficie. En el ejemplo de la figura se ha desplazado el vértice c_3,3 de una superficie de bigrado (2,2) y 5x5 tramos. Ejemplo.

Al aumentar un peso, la superficie se acerca al vértice correspondiente de la malla. Ejemplo.

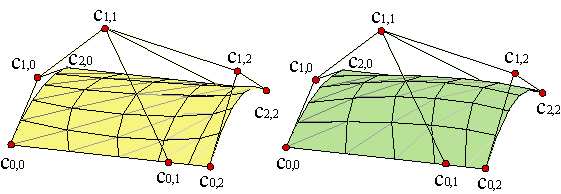
La principal cortapisa de la representación producto son las limitaciones que impone a la topología de las superficies. Cuando se trata de superficies abiertas, no hay mayor problema. Pero cuando se trata de superficies cerradas, las únicas topologías permitidas son la del cilindro y la del toro. Para representar la esfera es preciso recurrir a mallas degeneradas en las que los vértices se solapan, por ejemplo, en los polos de la esfera.

4 Algoritmo de de Casteljau

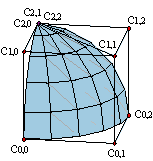
Vídeo de Algoritmo de De Casteljau y elevación del grado

Extender el algoritmo de de Casteljau a superficies es poco menos que una obviedad. Sólo tenemos que aplicarlo por separado a las columnas de la malla de control, como si fueran polígonos de curvas de grado m,

c^r,0)_i,j(u): = (1-u) c^r-1,0)_i,j(u)+uc^r-1,0)_i+1,j(u) ,

i = 0,..., m-r , r = 1,...,m , j = 1,...,n ,

(8)

hasta llegar a un único punto en la iteración m-ésima en cada columna, {c^m,0)_0,0(u),...,c^m,0)_0,n(u)}, que podemos considerar como un polígono de control de una curva de grado n, al cual volvemos a aplicar el algoritmo de de Casteljau,

c^m,s)_0,j(u,v): = (1-v) c^m,s-1)_0,j(u,v)+vc^m,s-1)_0,j+1(u,v) ,

j = 0,..., n-s , s = 1,...,n ,

(9)

hasta llegar al último paso de la iteración, que nos proporciona el punto c(u,v) de la superficie,

c(u,v) = c^m,n)_0,0(u,v) .

(10)

Obviamente el proceso es simétrico. Podíamos haber comenzado aplicando el algoritmo de de Casteljau a las filas.

La polar de una superficie de Bézier tampoco causa mayores problemas,

c[u₁,...,u_m;v₁,..., v_n]: = c[u₁,...,u_m][v₁,..., v_n] = c[v₁,..., v_n][u₁,...,u_m] ,

(11)

es decir, evaluamos la polar primero en u₁,...,u_m en cada de una de las columnas de la malla de control y, con el polígono resultante de grado n, evaluamos en v₁,...,v_n. O a la inversa, evaluamos en las filas en v₁,...,v_n y luego, en la columna resultante, en u₁,...,u_m.

Por ejemplo, si queremos restringir una superficie parametrizada, c(u,v), al recinto [a,b]x[c,d], la malla de control, {c'_0,0,..., c'_m,n}, de la nueva superficie es ,

c'_i,j = c[a^{< m-i >},b^{< i >};c^{< n-j >},d^{< j >}] .

(12)

Ejemplo.

5 Elevación del grado

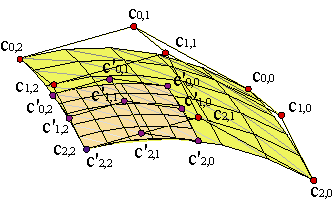
Vídeo de Algoritmo de De Casteljau y elevación del grado

Si tenemos una malla de control de bigrado (m,n), {c_0,0,...,c_m,n} y queremos expresar la superficie como si fuera de bigrado (m+1,n), no tenemos más que aplicar el algoritmo de elevación del grado independientemente a las n+1 columnas de la malla de control,

c(u,v) = Σ_{i = 0}^mΣ_{j = 0}ⁿc_i,jB^m_i(u)Bⁿ_j(v) = Σ_{i = 0}^m+1Σ_{j = 0}ⁿc^1,0_i,jB^m+1_i(u)Bⁿ_j(v) ,

(13)

c^1,0_i,j = (1-

m+1

)c_i,j+

m+1

c_i-1,j ,

(14)

y de manera análoga, si queremos elevar el bigrado a (m,n+1), aplicamos el algoritmo a las m+1 filas de la malla de control por separado,

c(u,v) = Σ_{i = 0}^mΣ_{j = 0}ⁿc_i,jB^m_i(u)Bⁿ_j(v) = Σ_{i = 0}^mΣ_{j = 0}ⁿ⁺¹c^0,1_i,jB^m_i(u)Bⁿ⁺¹_j(v)

(15)

c^0,1_i,j = (1-

n+1

)c_i,j+

n+1

c_i,j-1 .

(16)

y, por supuesto, podemos extender también el resto de fórmulas basadas en la polar o en la elevación sucesiva del grado. Ejemplo. Ejemplo.

6 Derivadas

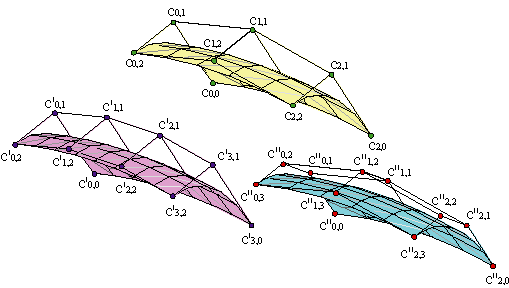
Vídeo de Uniones de curvas y twists

Dado que la base de funciones polinómicas que empleamos, B^m_i(u)Bⁿ_j(v) es separable en las variables u,v, las expresiones de las derivadas parciales de la parametrización no sufren grandes cambios respecto a las estudiadas para curvas de Bézier. Por ejemplo, la derivada con respecto a u,

∂c(u,v)

∂u

= mΣ_{j = 0}ⁿΣ_{i = 0}^m-1Δ^1,0 c_i,jB^m-1_i(u)Bⁿ_j(v) ,

(17)

donde hemos introducido las diferencias en los subíndices,

Δ^i,j c_i,j = Δ^i-1,j c_i+1,j-Δ^i-1,j c_i,j = Δ^i,j-1 c_i,j+1-Δ^i,j-1 c_i,j ,

cuyos primeros valores son generalización directa de las diferencias en un único índice,

Δ^1,0 c_i,j = c_i+1,j- c_i,j , Δ^0,1 c_i,j = c_i,j+1- c_i,j .

De manera análoga, la expresión de la derivada parcial respecto a v es

∂c(u,v)

∂v

= nΣ_{i = 0}^mΣ_{j = 0}^n-1Δ^0,1 c_i,jB^m_i(u)B^n-1_j(v) ,

(18)

y la generalización a derivadas superiores es inmediata,

∂^r+s c(u,v)

∂u^r ∂v^s

m! n!

(m-r)!(n-s)!

Σ_{i = 0}^m-rΣ_{j = 0}^n-sΔ^r,sc_i,jB^m-r_i(u)B^n-s_j(v) .

(19)

Especialmente interesantes son las derivadas en los bordes de la superficie, formado por los cuatros tramos u = 0, u = 1, v = 0, v = 1. Consideraremos uno de ellos, u = 0. Las derivadas parciales con respecto a la variable v corresponden a las derivadas tangenciales a la curva c(0,v). La novedad es la aparición de las derivadas transversales al borde, como son las parciales con respecto a u,

∂^r c(u,v)

∂u^r

¦_{u = 0} =

(m-r)!

Σ_{j = 0}ⁿΔ^r,0c_0,jBⁿ_j(v) .

(20)

Por ejemplo, en u = 1,

∂^r c(u,v)

∂u^r

¦_{u = 1} =

(m-r)!

Σ_{j = 0}ⁿΔ^r,0c_m-r,jBⁿ_j(v) .

(21)

Este resultado nos permite interpretar las hileras interiores de vértices de la malla. La primera hilera define el borde, la segunda la tangente y así sucesivamente.

Necesitaremos estos resultados para construir superficies polinómicas a trozos. Supongamos que tenemos dos superficies de Bézier parametrizadas respectivamente por c(u,v), c'(u,v) en los recintos [u₀,u₁]x[v₀,v₁], [u₁,u₂]x[v₀,v₁], con mallas de control {c_0,0,..., c_m,n} y { c'_0,0,..., c'_m,n}.

Si queremos que las superficies estén unidas por el borde u = u₁, la condición de continuidad exige que las curvas c(u₁,v), c'(u₁,v) sean idénticas, lo cual se consigue si la última fila de la malla de la primera superficie y la primera fila de la segunda son coincidentes,

c(u₁,v) = c'(u₁,v) implica c_m,j = c'_0,j j = 0,...,n .

(22)

Para establecer la clase de diferenciabilidad, sólo tenemos que preocuparnos de las derivadas transversales.

La condición para que la superficie compuesta sea de clase C¹ se obtiene a partir de (20-21),

∂c(u,v)

∂u

¦_{u = u₁} =

∂ c'(u,v)

∂u

¦_{u = u₁}

Δ^1,0c_m-1,j

Δu₀

Δ^1,0 c'_0,j

Δu₁

, j = 0,...,n .

(23)

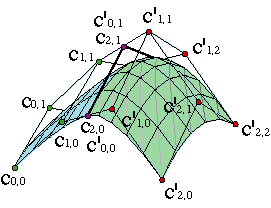
Podemos interpretarla pensando en las columnas de las mallas {c_0,j,..., c_m,j}, { c'_0,j,..., c'_m,j} como polígonos de control de curvas compuestas a las cuales estamos imponiendo la condición de tener derivada continua.

De este modo, la condición de ser de clase C¹ afecta a la franja de vértices de las mallas formada por las dos últimas filas de la primera superficie y las dos primeras filas de la segunda.

Sin embargo, esta buena propiedad se pierde en las superficies. Si imponemos en lugar de (23) que las parejas de vectores Δ^1,0 c_m,j, Δ^1,0 c'_0,j sean paralelas dos a dos, obtenemos una superficie que, en general, no tiene ni siquiera plano tangente bien definido en los puntos del borde, salvo en los extremos, como se comprueba calculando la normal en el borde.

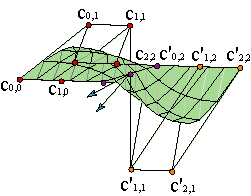
Generalizando este resultado, imponer que la superficie compuesta sea de clase C^r involucra a las r+1 filas adyacentes de cada malla de control y se refleja en la condición,

Δ^r,0c_m-r,j

(Δu₀)^r

Δ^r,0 c'_0,j

(Δu₁)^r

, j = 0,...,n .

(24)

Otras derivadas interesantes son las derivadas segundas cruzadas, que normalmente en el diseño se suelen llamar twists. En función de los vértices de la malla de control,

∂² c(u,v)

∂u ∂v

= mnΣ_{i = 0}^m-1Σ_{j = 0}^n-1Δ^1,1c_i,jB^m-1_i(u)B^n-1_j(v) ,

(25)

podemos escribir los coeficientes de manera que tengan una interpretación geométrica sencilla,

Δ^1,1c_i,j = c_i+1,j+1-a_i,j = c_i+1,j+1-c_i+1,j-c_i,j+1+c_i,j ,

a_i,j = c_i+1,j+c_i,j+1-c_i,j = c_i,j+c_i,jc_i+1,j+c_i,jc_i,j+1 .

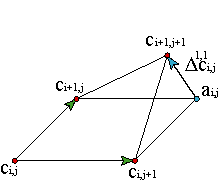
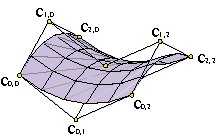
El vector Δ^1,1c_i,j representa la separación del vértice c_i+1,j+1 respecto del paralelogramo que determinan c_i,j, c_i+1,j,c_i,j+1,a_i,j.

En las esquinas del borde de la superficie, por ejemplo, en c_0,0, el twist es proporcional a Δ^1,1c_0,0 y, como los vectores c_0,0c_1,0, c_0,0c_0,1 determinan el plano tangente a la superficie en c_0,0, tenemos que dicho twist mide la separación del vértice c_1,1 del plano tangente a la superficie en c_0,0.

Pensemos en una superficie de Bézier bicúbica. Su malla de control posee dieciséis vértices, de los cuales doce, los externos, están determinados por las curvas que delimitan su borde. Sólo quedan libres los cuatro vértices interiores, que quedan determinados precisamente si fijamos los twists de las esquinas. Por tanto, la elección de los twists es fundamental para determinar la superficie que llena el espacio entre las cuatro curvas. De ahí su importancia. Ejemplo. Ejemplo.

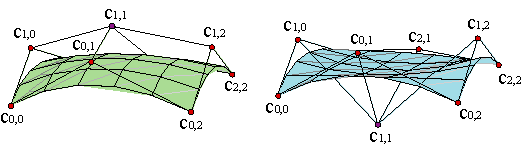
La opción más sencilla para escoger los twists es tomarlos nulos. Las superficies con todos los twists nulos se denominan superficies traslacionales. Ejemplo.

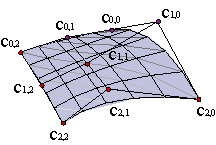
Las derivadas de la parametrización nos sirven asimismo para construir vectores normales en cada punto de la superficie. Dado que las derivadas parciales con respecto a u y a v definen vectores tangentes a la superficie, su producto vectorial define un vector normal en el punto c(u,v),

n(u,v) =

∂c(u,v)

∂u

∂c(u,v)

∂v

que podemos hacer unitario dividiéndolo por su norma.

Esta expresión supone un aumento considerable del grado con respecto al de la superficie. No es válida en los puntos en los que las derivadas parciales sean paralelas o nulas, lo cual no siempre quiere decir que la normal no esté bien definida, sino que puede ser un problema de la parametrización empleada.

Por ejemplo, la esfera tiene normal definida en el polo, pero no la podemos calcular ingenuamente por culpa del vértice múltiple.

La expresión se simplifica notablemente en las esquinas de la superficie, ya que involucran pocas diferencias de vértices. Por ejemplo, en c_0,0 = c(0,0),

n(0,0) = Δ^1,0c_0,0xΔ^0,1c_0,0 ,

(26)

si hubiera dos vértices iguales o los vértices c_0,0, c_0,1, c_1,0 estuvieran alineados, la fórmula anterior no nos proporcionaría la normal. fig529

7 Interpolación y aproximación

Vídeo de Interpolación y aproximación de superficies

Supongamos que tenemos una nube de (m+1)·(n+1) datos en el espacio, {a_0,0,..., a_m,n}, por los cuales queremos que pase por una superficie, c(u,v), para valores determinados de dos parámetros u,v,

a_i,j = c(u_i,v_j) , i = 0,...,m j = 0,...,n .

(27)

Intentaremos ajustarlos con una parametrización producto de una superficie de bigrado (m,n). En vez de atacar el problema como un sistema lineal de (m+1)·(n+1) incógnitas, los vértices de la malla de control, haremos uso del producto de polinomios para escribirlo como B_UCB_V^t = A,

A = (

a_0,0

...

a_0,n

^··_·

a_m,0

...

a_m,n

) ,

B_U = (

B^m₀(u₀)

...

B^m_m(u₀)

^··_·

B^m₀(u_m)

...

B^m_m(u_m)

)

C = (

c_0,0

...

c_0,n

^··_·

c_m,0

...

c_m,n

) ,

B_V = (

Bⁿ₀(v₀)

...

Bⁿ_n(v₀)

^··_·

Bⁿ₀(v_n)

...

Bⁿ_n(v_n)

) ,

donde las matrices A,C definen tres sistemas lineales, uno por cada coordenada de los puntos.

Las coordenadas de los vértices de la malla de control se obtienen formalmente invirtiendo las matrices, C = B_U^-1A(B_V^t)^-1. Aunque es más sencillo reducir el problema al ya estudiado de las curvas interpolantes, definiendo matrices auxiliares C': = B_UC, que serán la incógnita del sistema C'B_V^t = A.

Nótese que con esta argucia hemos reducido el problema inicial, un sistema lineal de (m+1)·(n+1) ecuaciones a dos sistemas, de (m+1) y (n+1) ecuaciones, respectivamente, con el consiguiente ahorro de operaciones. Ejemplo.

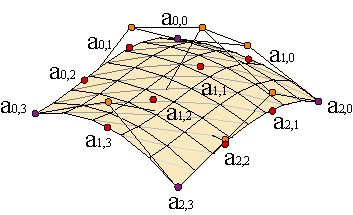
Otra opción, mucho más frecuente, es interpolar mediante superficies B-spline bicúbicas. El planteamiento es esencialmente el mismo, sólo hay que sustituir en nuestro sistema los polinomios de Bernstein por funciones B-spline.

Supongamos que nuestros datos deben verificar a_i,j = c(u_i,v_j), para i = 0,...,M, j = 0,...,N. Podemos fijar u_i e interpolar mediante un spline cúbico los puntos de la fila correspondiente, {a_i,0,...,a_i,N}. Obtenemos M+1 polígonos B-spline, uno por cada fila, que forman una matriz de puntos { d'_0,0,..., d'_M,N+2}. Interpolamos con splines cúbicos cada columna { d'_0,j,..., d'_M,j} y obtenemos una familia de N+3 polígonos B-spline, {d_0,0,..., d_M+2,N+2}, que constituyen la malla B-spline de la superficie interpolante. Las sucesiones de nudos son las propias {u₀,..., u_M}, {v₀,..., v_N}, con los nudos inicial y final repetidos tres veces. Obviamente, hace falta imponer condiciones en los extremos para que el problema de interpolación tenga solución única. Ejemplo.

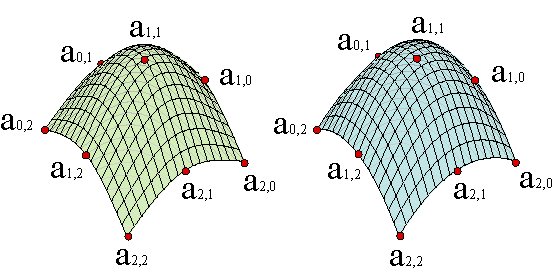
También podríamos haber resuelto el problema interpolando primero las columnas de datos y después las filas de vértices obtenidos.

En general, no es de esperar que nuestros datos estén organizados en el espacio de acuerdo a un patrón establecido, menos aún una malla aproximadamente rectangular. Lo usual es que debamos asignar a cada dato a_i unos parámetros (u_i,v_i) que no estén situados sobre una malla rectangular.

Consideremos el problema de aproximación, en el cual queremos obtener una superficie de bigrado (m,n) que aproxime un conjunto de datos, {a₀,...,a_M}, tales que a_i = c(u_i,v_i). El sistema lineal del problema,

(

B^m₀(u₀)Bⁿ₀(v₀)

...

B^m_m(u₀)Bⁿ_n(v₀)

^··_·

B^m₀(u_M)Bⁿ₀(v_M)

...

B^m_m(u_M)Bⁿ_n(v_M)

)(

c_0,0

c_m,n

) = (

a₀

a_M

) ,

(28)

tiene (m+1)·(n+1) incógnitas para M+1 ecuaciones, así que para un número alto de datos, el sistema está sobredeterminado.

Recurrimos, pues, a la aproximación por mínimos cuadrados. Si escribimos nuestro sistema como BC = A, lo podemos transformar, como hicimos en el problema equivalente para curvas, en un problema de (m+1)·(n+1) ecuaciones e incógnitas,

B^tBC = B^tA ,

(29)

que, en principio, es abordable, aunque para un número elevado de datos el sistema está mal condicionado y no es soluble numéricamente. fig534

No es común tener los parámetros (u_i,v_i) de los datos, sino que el diseñador tendrá que imponerlos de alguna manera eficiente. Esta es una tarea ardua y complicada.

Una opción sería proyectar los puntos sobre un plano, por ejemplo, el XY y leer las coordenadas (x_i,y_i) de los datos como parámetros, transformándolos si es preciso mediante un cambio de escala para que estén contenidos en nuestro dominio, el cuadrado [0,1]x[0,1].