En el tema anterior estudiamos que una manera de superar la rigidez de las curvas de Bézier consistía en recurrir a curvas racionales. Aún así, la flexibilidad que proporcionan los pesos de las curvas racionales es muy limitada. En vez de tratar de cubrir toda la curva con una sola parametrización polinómica o racional, emplearemos varias. De esta manera conseguiremos mayor flexibilidad, ya que, modificando una parametrización, sólo alteraremos la parte de la gráfica correspondiente a esta.
Estudiaremos inicialmente como construir parábolas de clase C1 a trozos y cúbicas de clase C2 y C1 a trozos antes de introducir un procedimiento general.
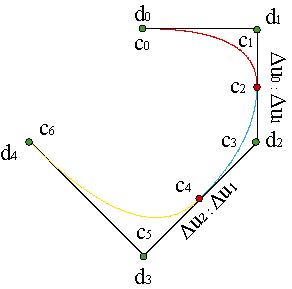
Consideremos una curva plana formada por N tramos parabólicos. Tendremos una colección de vértices {c0,..., c2N}, en la cual {c0,c1,c2} es el polígono de control del primer tramo, {c2,c3,c4} es el polígono del segundo, {c2(i-1),c2i-1,c2i}, el del i-ésimo, y {c2N-2,c2N-1,c2N}, el del último.
Cada polígono definirá una parametrización en un intervalo. Así el primer tramo estará definido en un intervalo [u0,u1], el segundo, en [u1,u2], el i-ésimo, en [ui-1,ui] y el último, en [uN-1,uN].
Si queremos que la curva compuesta sea de clase C1 en todo el intervalo [u0,uN], tal como se estudió en el tema segundo, tendremos que exigir que lo sea para cada valor u = ui,
| (1) |

Las relaciones (1) no se mantienen si permitimos al usuario modificar todos los vértices. Por tanto, si queremos mantener la clase de diferenciabilidad, sólo deberemos ofrecerle los vértices que no afecten a dicha condición.
Con esta idea en mente, podemos ver (1) como la definición del vértice c2i, conocidos los vértices c2i-1, c2i+1,
| (2) |
En resumen, los únicos datos de la curva que debemos facilitar al usuario para que los modifique libremente, sin alterar la condición de suavidad, son los nudos de la partición del intervalo, {u0,..., uN} y los vértices de los polígonos de control {c0,c1,...,c2i-1,..., c2N-1,c2N}, es decir, un total de N+2 vértices, como corresponde al hecho de que tenemos 2N+1 vértices y N-1 condiciones de diferenciabilidad en las uniones. Ejemplo
Vídeo de Ejemplo de tramo parabólico spline
Adelantando notación posterior, denotaremos como {d0,...,dN+1} estos vértices,
| (3) |
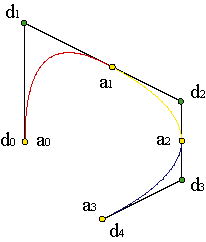
Esta construcción de la curva de clase C1 parabólica a trozos se puede emplear para interpolar una curva de clase C1 entre N+1 puntos del plano, a0,...,aN, por los que sabemos que pasa para valores conocidos del parámetro u, ai = c(ui). El problema se reduce a resolver el sistema de ecuaciones c2i = ai,
| |||||||||||||||||||||||
Si la curva es cerrada, c0 = c2N+2, todo vértice par se obtiene a partir de los impares adyacentes por la relación (2) y sólo es preciso facilitar estos últimos, {c1,...,c2i-1,...,c2N+1}. El vértice inicial-final se obtiene como caso particular,
| ||||||||||||||||||||||
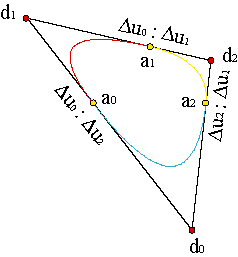
El polígono B-spline, {d0,...,dN}, está formado por los vértices interiores, d0 = c2N+1, di = c2i-1, i = 1,...,N.
La matriz de este problema es regular para N par. Luego tenemos garantizada la solución única del problema de interpolación exclusivamente para un número impar de puntos, lo cual no quiere decir que no haya solución en todos los casos. Luego no es un método afortunado de interpolación. Ejemplo
Es claro que, como la parábola es una curva plana, esta construcción sólo es válida en el plano.
Para abordar el problema de interpolación en el espacio, debemos recurrir a cúbicas. Buscaremos construir una curva de clase C2 de N tramos. Tendremos, pues, como vértices de los sucesivos polígonos de control {c0,...,c3N}, de los cuales {c3(i-1),c3i-2,c3i-1,c3i} corresponden al tramo i-ésimo, definido en el intervalo [ui-1,ui].
Vamos a imponer que la parametrización sea de clase C2 en u = ui, unión de los tramos i e (i+1)-ésimo. Como en el apartado anterior, la condición de ser de clase C1 se traduce en
| (6) |
| (7) |
Finalmente, la condición de continuidad de las derivadas segundas, desarrollada en el tema segundo, aplicada al nudo ui nos proporciona como información que los vectores c3i-2c3i-1 y c3i-1di están en proporción Δui-1:Δui, igual que los vectores di c3i+1 y c3i+1 c3i+2.
Aplicando esta misma condición al nudo ui+1 obtenemos otra relación. Los vectores c3i+1c3i+2 y c3i+2di+1 están en proporción Δui:Δui+1. Y del nudo ui-1 extraemos que di-1 c3i-2 y c3i-2c3i-1 guardan una proporción igual a Δui-2:Δui-1.
Con toda esta información, estamos en condiciones de expresar los vértices c3i-1, c3i+1 en términos de los nuevos puntos que hemos introducido,
| ||||||||||||||||||||||
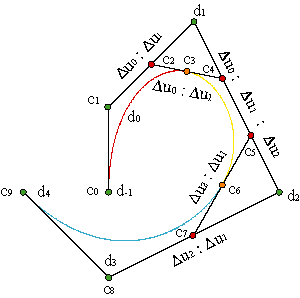
Este resultado, combinado con (7) nos permite obtener todos los vértices de la curva compuesta a partir de los puntos d1,...,dN-1, garantizando que la parametrización es de clase C2. Quedan fuera los vértices que no son adyacentes a ninguna unión, es decir, los vértices iniciales, c0, c1, y finales, c3N-1, c3N, que no pueden obtenerse por estas relaciones.
Denotaremos, como hicimos en el apartado anterior, d-1: = c0, d0: = c1, dN: = c3N-1, dN+1: = c3N, para poder completar la relación de vértices. Los restantes vértices, c2, c3N-2 se obtienen a partir de (8) tomando Δu-1 y ΔuN nulos.
Realmente, la notación usual es la correlativa de 0 hasta N+2, para lo cual deberíamos adelantar los índices en una unidad. Esta será la notación que vamos a seguir.
Una vez más, en el caso de curvas cerradas, no hace falta añadir más puntos y todos los vértices se obtienen a partir de (7) y (8).
Por ello, podemos codificar la curva compuesta por medio del polígono de control B-spline, {d0,...,dN+2} y la sucesión de nudos {u0,...,uN} de modo que el usuario podrá modificar la forma de la curva sin alterar sus propiedades de diferenciabilidad.
Sustituyendo las expresiones de los vértices c3i-1 y c3i+1 en (7),
| ||||||||||
| ||||||||||
| ||||||||||||
| |||||||||||
Esta relación es útil para resolver el problema de interpolación: dados N+1 puntos a0,..., aN y los nudos {u0,...,uN}, obtener la curva de clase C2 cúbica a trozos que verifique c(ui) = ai. El problema se reduce al sistema lineal (9), donde los datos son c0 = d0 = a0, c3i = ai, i = 1,...,N-1, aN = dN+2 = c3N y las incógnitas son los vértices del polígono B-spline, {d0,...,dN+2}. Tenemos, pues, N+3 incógnitas para N+1 datos, así que el sistema tiene dos parámetros libres, por ejemplo, d1 y dN+1. Se puede demostrar que el sistema tiene rango N+1, así que el problema tiene solución única, una vez introducidos los valores de los vértices libres.
Existen varias maneras de fijar estos vértices, imponiendo condiciones razonables a la curva.
Una posibilidad son las condiciones naturales, que imitan el comportamiento físico del junquillo, el cual tiende a ser recto en los extremos. Por tanto, la condición natural es
| (10) |
No obstante, estas condiciones no son muy apreciadas en el diseño, precisamente porque provocan que los extremos de las curvas sean excesivamente rectos.
Otra opción consiste en elegir las tangentes en los extremos, c'(u0), c'(uN), que determinan a su vez los vértices d1, dN+1,
| ||||||||
| |||||||||
Una manera práctica de prescribir las tangentes son las condiciones de Bessel, que consisten en tomar como valor de c'(u0) la derivada en el origen de la parábola que pasa por los puntos a0, a1, a2 y, análogamente, c'(uN) será la derivada en uN de la parábola que interpola aN-2, aN-1, aN.
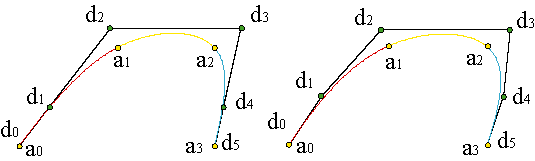
Las tangentes de Bessel proporcionan resultados mucho mejores que la condición natural. Ejemplo
En el caso de curvas cerradas, como se ha indicado, no son precisos vértices ni datos adicionales y el sistema se cerraría en forma periódica.
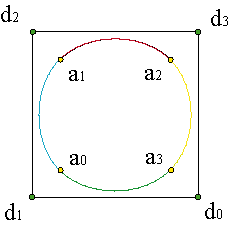
Generalizando lo aprendido en estos apartados, para construir curvas de grado n en N tramos de clase Cn-1, las cuentas están claras: las curvas de Bézier aportan nN+1 vértices de sus polígonos de control, pero tenemos n-1 condiciones de diferenciabilidad en las N-1 uniones. Por tanto, el monto de parámetros libres es nN+1-(N-1)(n-1) = N+n.
Un problema alternativo al anterior sería la interpolación con cúbicas, conocidos los puntos de la curva c(ui) y las tangentes a la curva, de clase C1 al menos en dichos puntos.
Supongamos que tenemos N+1 puntos {a0,...,aN} y N+1 vectores {v0,...,vN} y queremos trazar una curva interpolante c(u) que verifique c(ui) = ai, c'(ui) = vi, i = 0,...,N para una sucesión creciente de valores del parámetro u, {u0,...,uN}.
Una solución sencilla para este problema nos la proporciona una cúbica a trozos de clase C1 con N tramos. Al igual que en el caso anterior, la curva requiere 3N+1 vértices {c0,...,c3N}, de los cuales N+1, los extremos de las cúbicas, están determinados por las condiciones c3i = ai, i = 0,..., N. El resto están determinados por las tangentes.
Teniendo en cuenta las expresiones para las derivadas en los extremos de cada cúbica, estudiadas previamente,
| |||||||||||||||||
| ||||||||||||||||||
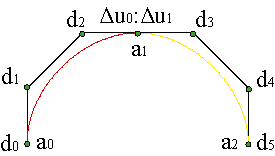
Sin embargo, para codificar la información de la curva, no es preciso una vez más dar todos los vértices, sino tan sólo los interiores, ya que los vértices exteriores se despejan de las relaciones anteriores, salvo los vértices inicial y final, c0, c3N. Por tanto, podemos caracterizar la curva por la sucesión de nudos {u0,..., uN} y los vértices del polígono B-spline, {d0,..., d2N+1}, dado por d0: = c0, d2i-1 = c3i-2, d2i = c3i-1, i = 1,..., N, d2N+1 = c3N,
| |||||||
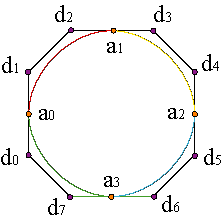
El caso de curvas cerradas que interpolen los N+1 puntos y tangentes es aún más sencillo: las expresiones (12-13) son válidas también para los casos extremos i = 0,N sin más que tomar Δu-1: = ΔuN, para lo cual necesitamos un nudo mas, uN+1, el que cierra la curva mediante las condiciones a0 = c(uN+1), v0 = c'(uN+1).
Consideremos una parábola parametrizada en un intervalo [u1,u2] por c(u). Usando la multiafinidad de la polar, podemos expresar c(u) como un paso del algoritmo de de Casteljau,
| ||||||||
| ||||||||||||||||||||||||||
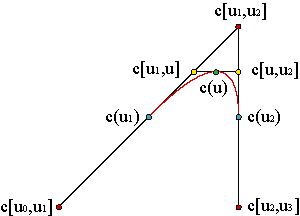
Nótese que, en el caso particular en el que u0 = u1, u3 = u2, recuperamos precisamente el algoritmo de de Casteljau original para el polígono de control {c0 = c[u1,u1], c1 = c[u1,u2], c2 = c[u2,u2]}.
Por tanto, lo que hemos hecho ha sido generalizar el algoritmo de de Casteljau, mediante la introducción de dos nudos auxiliares. Para que todos los sumandos sean positivos en la parametrización, esta estará definida en el intervalo [u1,u2]. El efecto de esta generalización es acortar la curva de Bézier que correspondería al polígono, lo que nos servirá para unirla a otros tramos de curvas polinómicas.
Resumiendo, los pasos seguidos en el algoritmo han sido:
| ||||||||||||||||||||
El polígono B-spline para la parábola estará formado por los vértices {d0: = c[u0,u1],d1: = c[u1,u2],d2: = c[u2,u3]}.
Este es el algoritmo de de Boor para una curva parabólica de un único tramo. El algoritmo se generaliza sin dificultad a curvas de cualquier grado, n, y un solo tramo. El polígono estará formado por n+1 vértices, como corresponde a una curva polinómica de grado n, {d0,...,dn}, donde di = c[ui,...,ui+n-1]. La sucesión de nudos estará formada por 2n valores del parámetro, {u0,...,u2n-1}. Ejemplo
Finalmente el algoritmo de de Boor consiste en la aplicación reiterada del algoritmo de de Casteljau,
| |||||||||||||||||||||||||||||||||||||||||
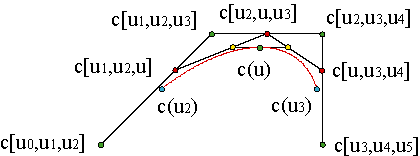
Por supuesto, c(u) = dn)0(u). La parametrización está definida en el intervalo final, [un-1,un]. Ejemplo
La forma polar correspondiente al algoritmo de de Boor se construye de manera trivial. Para el polígono correspondiente a una curva de grado n, {d0,...,dn}, y una sucesión de nudos, {u0,...,u2n-1}, la polar se evalúa en los valores v1,...,vn del parámetro,
| ||||||||
| ||||||||||||
| ||||||||
| ||||||||||
| ||||||||||
| ||||||||
| ||||||||||
| |||||||||||
A pesar de su aparente asimetría, la polar sigue siendo simétrica.
Obviamente, la polar devuelve los valores correctos de los vértices del polígono de control, Ejemplo, Ejemplo
| ||||
En el fondo, lo único que hemos hecho al introducir el algoritmo de de Boor para curvas polinómicas de un sólo tramo es cambiar el conjunto de puntos con los cuales calculábamos la polar. Pasamos de {c0,...,cn} para el algoritmo de de Casteljau a {d0,...,dn} con el algoritmo de de Boor. Pero la polar sigue siendo la misma.
La polar nos proporciona un sencillo mecanismo para pasar de un esquema a otro. Por ejemplo, si tenemos el polígono B-spline de una curva de grado n, {d0,...,dn}, su polígono de control, como curva de Bézier vendrá dado simplemente por
| ||||
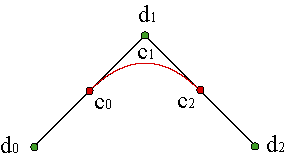
A este nivel puede parecer un esfuerzo innecesario el que estamos realizando al cambiar de representación, pero el apartado siguiente nos permitirá avanzar hacia las curvas de varios tramos.
El algoritmo de de Boor se puede extender a curvas compuestas de N tramos polinómicos de grado n, que es para lo que estaba ideado inicialmente. Consideremos una colección de vértices {d0,...,dn+N-1} y una sucesión de nudos {u0,...,u2n+N-2}. El primer tramo de curva está parametrizado en el intervalo [un-1,un], de acuerdo con el algoritmo ya estudiado, por los vértices {d0,..., dn} y los nudos {u0,...,u2n-1}. Y así sucesivamente, el tramo i-ésimo tiene por polígono {di-1,..., dn+i-1}, sucesión de nudos {ui-1,..., u2n+i-2} y su intervalo de definición es [un+i-2,un+i-1]. Finalmente, el último tramo de curva tiene por polígono {dN-1,...,dn+N-1}, nudos {uN-1,...,u2n+N-2} y está definido en [un+N-2,un+N-1]. Ejemplo
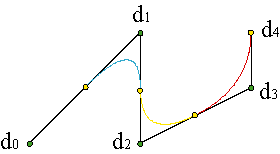
Así pues, una curva de N tramos y grado n tiene n+N vértices y 2n+N-1 nudos y está definida en el intervalo [un-1,un+N-1]. Los n-1 nudos iniciales y finales son auxiliares. Lo normal es tomarlos iguales al nudo inicial o final, respectivamente, u0 = ... = un-1, un+N-1 = ... = u2n+N-2, tal como hicimos, sin indicarlo, en los apartados precedentes, donde no aparecían tales nudos auxiliares. El motivo no es otro que forzar a la curva a pasar por los vértices inicial y final, d0 = c(un-1), dn+N-1 = c(un+N-1).
Como es fácil de imaginar, la repetición de un nudo no auxiliar, por ejemplo, uI = uI+1, supone la desaparición del tramo de curva correspondiente, en este caso el (I-n+1)-ésimo, que queda reducido a un punto. También supone rebajar en una unidad la clase de diferenciabilidad de la curva en dicha unión.
Sólo resta, pues, saber cómo aplicar el algoritmo de de Boor a cada uno de los tramos para construir la curva compuesta.
Supongamos que queremos evaluar la curva en un valor u del parámetro. Tendremos que averiguar en qué intervalo [uI,uI+1) está contenido y aplicar el algoritmo de de Boor al polígono correspondiente a ese tramo, { d'0: = dI-n+1,...,d'n: = dI+1} y a los nudos u'0: = uI-n+1,..., u'2n-1: = uI+n, tal como se explica en (16).
La extensión a curvas racionales a trozos es bastante sencilla, pues, como vimos en el tema anterior, las parametrizaciones racionales en An se obtienen a partir de parametrizaciones polinómicas en Rn+1, donde la componente adicional corresponde al denominador de la parametrización. Así pues, introduciendo una componente más, el algoritmo de de Boor es aplicable a curvas racionales, sin más que dividir por la coordenada adicional.
Vídeo de Propiedades de las curvas spline
El algoritmo de de Boor expresa que las parametrizaciones de las curvas polinómicas a trozos son combinaciones baricéntricas de los vértices del polígono B-spline, así que disfrutan de las mismas propiedades que las curvas de Bézier. En el caso de las curvas racionales, se mantiene la invariancia proyectiva. Otras, como pasar por los vértices inicial y final, dependen de la elección de los nudos auxiliares. Ejemplo
Como en el algoritmo de de Boor sólo intervienen cocientes de diferencias de valores del parámetro u, la parametrización es insensible a cambios afines de parámetro u' = a u+b, siempre que transformemos los nudos de idéntica manera, u'i = a ui+b, i = 0,..., 2n+N-2.
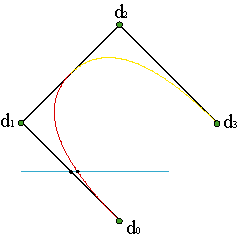
Más aún, como en cada intervalo las curvas spline son curvas polinómicas, gozan de las propiedades que ya estudiamos para estas, no sólo globalmente, sino en cada tramo concreto. Así cada tramo de curva, por ejemplo el i-ésimo, está contenido en la envolvente convexa de su polígono de control, {di-1,...,di+n-1}. Lo mismo sucede con la propiedad de la disminución de la variación. Una recta corta al tramo i-ésimo de la curva en a lo sumo tantos puntos como al polígono de control de dicho tramo. Ejemplo.
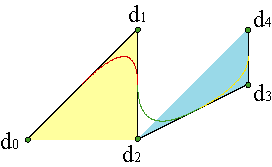
Finalmente, hay propiedades que presentan una mejora sustancial. Cada tramo de la curva depende exclusivamente de los n+1 vértices de su polígono de control. Por tanto, no se ve afectado por los cambios de los demás vértices. Visto de otro modo, un vértice genérico di está presente en los polígonos de control de todos los tramos desde el (i-n+1)-ésimo, {di-n,...,di}, hasta el (i+1)-ésimo, {di,...,di+n}. Así pues, un desplazamiento del vértice di modifica tan sólo a un total de n+1 tramos de la curva. Obviamente, si el vértice está próximo al comienzo o al final del polígono, controlará un número inferior de tramos. A esta propiedad se la denomina control local y no existía para las curvas de Bézier, donde la modificación de un vértices afectaba a toda la curva. Ejemplo. Ejemplo
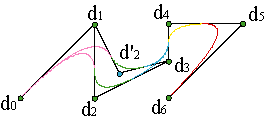
Vídeo de Algoritmo de inserción de nudos y elevación del grado
Íntimamente ligado al algoritmo de de Boor está el algoritmo de inserción de nudos. Esencialmente es el equivalente del algoritmo de subdivisión estudiado para el algoritmo de de Casteljau.
Consideremos un polígono de control B-spline para una curva de grado n de N tramos, {d0,...,dn+N-1} y una sucesión de nudos {u0,...,u2n+N-2}, en la cual queremos introducir un nudo adicional u', distinto o igual a alguno de los originales, de modo que la gráfica de la curva permanezca invariable. Como el número de vértices, L+1 y el número de nudos, K+1, están ligados entre sí, K = L+n-1, la inclusión del nuevo nudo supone la aparición de un tramo nuevo de curva, es decir, una subdivisión, y, por tanto, un nuevo vértice.
Si en la nueva sucesión ordenada de vértices, { u'0,...,u'2n+N-1}, el nuevo nudo ocupa la posición i-ésima,
| |||||||||||||
| |||||
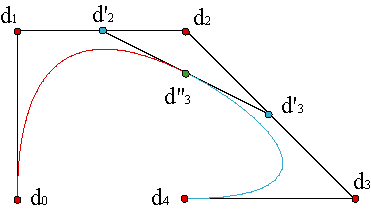
La aplicación reiterada del algoritmo de inserción de los nudos ui,ui+1 hasta que alcancen ambos la multiplicidad n es una manera equivalente de obtener el polígono de control de la curva en el intervalo [ui,ui+1]. Ejemplo. Esto es obvio, ya que la sucesión de nudos de dicho intervalo, después de la inserción será {ui < n > , ui+1 < n > } que corresponde, como sabemos, a una curva de Bézier, con vértices ci = d[ui < n-i > , ui+1 < i > ].
Vídeo de Algoritmo de inserción de nudos y elevación del grado
En el tema segundo demostramos la expresión de la elevación del grado,
| |||||||
La fórmula (19) está pensada para curvas de Bézier y, por tanto, no hace referencia a ninguna sucesión de nudos. Pero es claro que, como la sucesión de nudos para estas curvas es de la forma {u0 < n > , u1 < n > } y la curva elevada sigue siendo de Bézier, pero de grado n+1, su sucesión de nudos será {u0 < n+1 > , u1 < n+1 > }. Por tanto, para elevar el grado, hay que usar la fórmula (19), pero teniendo en cuenta que hay que duplicar todos los nudos interiores, los que definen los tramos de la curva, desde un-1 hasta un+N-1. Ejemplo, Ejemplo.
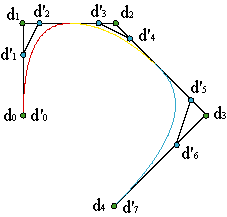
Por tanto, para elevar el grado de una curva polinómica de grado n a trozos, basta emplear la fórmula (19), por ejemplo para calcular el polígono B-spline, con la sucesión de nudos,
| |||||
Vídeo de Derivadas de curvas spline
En el primer tema demostramos que las derivadas de una curva de Bézier se podían expresar por medio de la polar,
| |||||||||
Esta expresión sigue siendo válida para cada tramo de una curva spline, ya que está basada en la polar. Por ejemplo, para la derivada primera en u ∊ [ui,ui+1],
| |||||||||||
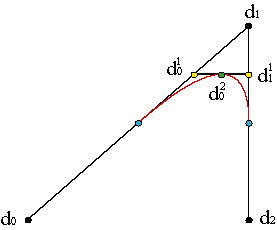
es decir, los vértices del último paso del algoritmo determinan la tangente a la curva en c(u). Ejemplo. Para derivadas superiores,
| |||||||||||
En este apartado vamos a volver sobre el tema ya mencionado varias veces de la diferenciabilidad de curvas polinómicas de grado n a trozos. La curva c(u) es de clase Cn-1 en ui, si este nudo es simple.
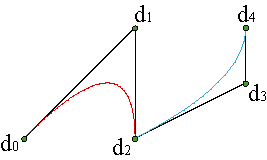
El caso de nudos múltiples no es mucho más complicado. En una unión de tramos en la que el nudo común de los intervalos tiene multiplicidad r, la curva es de clase al menos Cn-r, pudiendo ser de clase superior, aunque genéricamente no lo sea. Ejemplo.
Este resultado es una muestra más de la versatilidad de las curvas polinómicas a trozos, que nos permiten combinar tramos con diferentes clases de diferenciabilidad sin más que repetir los nudos de las uniones.
Del mismo modo que la aplicación del algoritmo de de Casteljau conduce a la aparición de los polinomios de Bernstein, el algoritmo de de Boor introduce funciones polinómicas en cada tramo.
Consideremos funciones polinómicas a trozos definidas en un intervalo [u0,um], con partición {u0,...,um}, de modo que en cada intervalo [ui,ui+1] las funciones son polinomios de grado n y en cada nudo ui son de clase Cn-ri. Estas funciones forman un espacio lineal.
La dimensión del espacio de funciones spline de grado n y N tramos es dim = n+N = 1+L, es decir, coincide con el número de vértices de los polígonos B-spline.
Esto está de acuerdo con la idea de que podemos codificar el algoritmo de de Boor en unas funciones {Nn0(u),..., NnL(u)}, base de dicho espacio, de modo que, si el polígono de una curva es {d0,..., dL},
| |||||
Para conseguir esto, debemos saber primero cómo construir funciones en vez de curvas paramétricas. Volvemos a expresar el monomio lineal u en nuestro formalismo. Para ello, hacemos uso de la forma polar. Si queremos expresarla con polinomios de grado uno, la respuesta es bien sencilla,
| ||||
| |||||||||
Por tanto, si queremos conocer el polígono B-spline, {ξ0,...,ξn+N-1}, del monomio lineal con una sucesión de nudos {u0,...,u2n+N-2}, grado n y N tramos, sólo tenemos que evaluar la polar,
| |||||||
A estos valores medios de los nudos se los conoce como abscisas de Greville.
Por tanto, si expresamos una función polinómica a trozos, f(u), como una gráfica, (u,f(u)), los vértices de su polígono B-spline serán de la forma (ξi,[d']i), donde [d']i son los vértices de la ''curva'' paramétrica f(u).
Con esta información, construimos las funciones nodales o B-spline, Nni(u), de grado sobre la sucesión de nudos {u0,...,u2n+N-2} como aquellas cuya gráfica tiene polinomio B-spline {di0,...,din+N-1}, donde dij = (ξj,Δij), es decir, la ordenada de todos los vértices es nula, salvo la correspondiente al índice i.
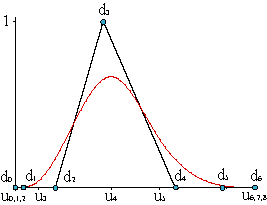
Así pues, {Δi0,...,Δin+N-1} es el polígono de la función nodal Nni(u). Por tanto {ΣdiΔi0,...,ΣdiΔin+N-1} = {d0,...,dn+N-1} es a la vez el polígono de c(u) y de ΣdiNni(u), luego hemos llegado a la expresión (24) y sólo hace falta deducir la forma exacta de las funciones nodales. Pero antes deduciremos propiedades generales de estas funciones.
Las funciones B-spline son polinómicas a trozos. Consideremos la gráfica de la función Nni(u) sobre una sucesión de nudos {u0,...,u2n+N-2}.
El soporte, el intervalo cerrado fuera del cual la función Nni(u) se anula, es [ui-1,ui+n]. Una propiedad importante de las funciones nodales es que el soporte es mínimo. No hay funciones no nulas con soporte más corto que el de las funciones nodales.
Tenemos tantas funciones nodales linealmente independientes como dimensión tiene el espacio de funciones polinómicas a trozos. Las funciones nodales forman base de dicho espacio.
Una propiedad importante de los polinomios de Bernstein, fuente de numerosas propiedades de la curvas de Bézier era que formaban una partición de la unidad. Esta propiedad se mantiene en la base de funciones nodales,
| (27) |
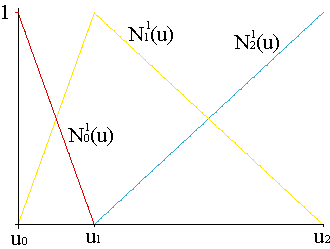
Finalmente, las funciones B-spline gozan de una propiedad de recursividad, que permite construirlas de forma iterativa a partir de las de menor grado,
| ||||||||||||||||||||||||||||
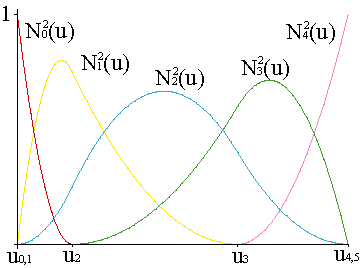
Como ya se ha comentado, la aplicación del algoritmo de de Boor a las curvas racionales sólo supone la introducción de una coordenada auxiliar, que da lugar al denominador de la parametrización.
Del mismo modo, una curva racional a trozos se puede expresar en términos de las funciones nodales sin más que introducir un denominador. Así pues, una curva racional de grado n a trozos y N tramos está determinada por los vértices de su polígono B-spline, {d0,...,dn+N-1}, sus correspondientes pesos, {w0,...,wn+N-1}, y una sucesión de nudos, {u0,...,u2n+N-2},
| ||||||
Todos los procesos que hemos descrito para curvas polinómicas a trozos, tales como inserción de nudos, elevación del grado u obtención de polígonos de control, se trasladan automáticamente a curvas racionales, sin más que introducir la coordenada auxiliar y luego proyectar.
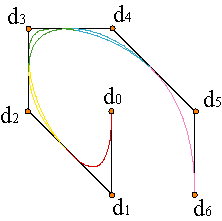
Dada la propiedad de localidad de las curvas spline, la modificación de un peso altera tan sólo a n+1 tramos de la curva. Ejemplo. Se mantienen las propiedades de las curvas racionales y, por supuesto, las de las curvas polinómicas a trozos.