1  Introducción

Vídeo de Curvas racionales

Las curvas polinómicas constituyen una sencilla herramienta para el diseño. Sin embargo, adolecen de cierta rigidez, ya que los polinomios tienen propiedades muy definidas, como tener a lo sumo tantas raíces como el grado, lo que coarta sobremanera su flexibilidad. Vemos como ejemplo, cómo aproxima una cúbica cinco puntos sobre una sinusoide:

La falta de flexibilidad de los polinomios también puede provocar, por contra, la aparición de tramos de elevada curvatura o con oscilaciones bruscas. Ejemplo.

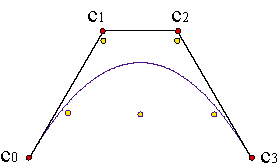
Por otra parte, el repertorio de curvas que pueden describirse exactamente por medio de parametrizaciones polinómicas es bastante limitado. El resultado de aproximar, por ejemplo, una circunferencia con tramos parabólicos no es siempre satisfactorio.

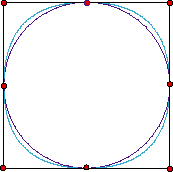
Una posibilidad, que consideraremos en el siguiente tema, es trabajar con curvas polinómicas a trozos. Otra es emplear curvas racionales.

2  Curvas racionales

Definiremos las parametrizaciones racionales de grado n como aquellas cuyas componentes son cocientes de polinomios de grado n.

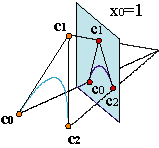
Consideremos una curva polinómica, (c₀(t),c₁(t),c₂(t)), t∊[0,1], en R³ y que no pase por el origen. Sabemos que se proyecta sobre el plano afín con una parametrización (c₁(t)/c₀(t),c₂(t)/c₀(t)).

Descompondremos las coordenadas de los vértices en dos partes, c_i = (w_i,w_ic_i), donde w_i es la primera componente del vértice i-ésimo y w_ic_i son las dos restantes (tres, si se tratara de una curva espacial). c_i es precisamente la proyección de c_i sobre el plano afín.

Estamos describiendo las curvas racionales por medio de un polígono de control {c₀,...,c_n} y unos parámetros, {w_i,...,w_n}, que denominaremos pesos.

Si todos los pesos son iguales, w = w_i, i = 0,...,n, el denominador desaparece y recuperamos una curva polinómica,

La exigencia de seguir trabajando con términos positivos nos limita a valores positivos de los pesos. En el diseño rara vez se emplean pesos de órdenes de magnitud distintos del de la unidad. Aquí vemos lo que sucede si tomamos un peso negativo. La curva tiene poco que ver con el polígono de control y no respeta la envolvente convexa de este.

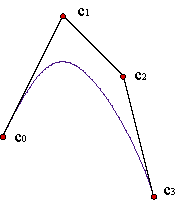
La interpretación de los pesos es bastante sencilla. Si hacemos crecer uno de los pesos, w_k, dejando fijos el resto, la curva tiende a acercarse al vértice, c_k, correspondiente. Ejemplo Este efecto se puede emplear para incrementar la tensión de la curva. Ejemplo

Sin embargo, si multiplicamos todos los pesos por un mismo número, la cancelación entre numerador y denominador deja la curva invariable. Ejemplo

Este hecho se puede utilizar para normalizar los pesos, por ejemplo, de modo que el primer peso valga la unidad.

¿Qué sucede si uno de los vértices c_i es un punto del infinito?

En este caso no tiene sentido hablar del peso w_i, ya que la primera componente del vértice va a ser nula, c_i = (0,c_i). Su imagen en el afín es un vector, no un punto, por lo que lo denominaremos vector de control. Haciendo esta distinción, la expresión de una curva racional queda así:

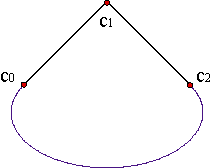
La presencia de vectores de control es bastante molesta, ya que, al no ser ya (2) una combinación baricéntrica de puntos, no va a mantenerse la propiedad de la envolvente convexa, entre otras. Ejemplo

2.1  Propiedades de las curvas racionales

Muchas de las propiedades de las curvas de Bézier se trasladan a las curvas racionales de manera inmediata, ya que seguimos empleando combinaciones baricéntricas de los vértices del polígono de control.

Las propiedades que se derivaban de este hecho, tales como que la curva esté contenida en la envolvente convexa del polígono de control, la disminución de la variación o que sea invariante bajo transformaciones afines, se mantienen. Ejemplo

Otras propiedades, como pasar por los vértices c₀, c_n o ser simétrica, se cumplen también.

Las curvas racionales son invariantes bajo transformaciones más generales, como son las transformaciones proyectivas. Si f es una transformación proyectiva del plano y {c₀,...,c_n}, {w₀,...,w_n} son el polígono de control y la lista de pesos de una parametrización racional, entonces

Una transformación proyectiva de la recta convierte una parametrización racional de grado n, c(t), en otra parametrización racional del mismo grado para la misma curva, c(t(u)),

Reparametrizaremos de modo que el intervalo final siga siendo el [0,1], lo cual se consigue con transformaciones de la forma

Con estas transformaciones, la parametrización se altera de manera sencilla. El efecto se traduce en un cambio de pesos {w'₀,...,w'_n}, w'_i = b^n-iw_i. manteniéndose el mismo polígono de control, {c₀,...,c_n}.

Existen varios juegos, infinitos, de pesos que proporcionan la misma curva racional. La gráfica no se altera, tan sólo la velocidad con la que se recorre la curva. Cuando b < 1, el efecto consiste en que la curva es recorrida más rápidamente al principio que al final. Cuando llegamos a u = 1/2, estamos más allá de t = 1/2 en la parametrización primitiva. Y al revés cuando b > 1. Ejemplo En la gráfica vemos t(u) para b=1/2, verde y b=2, rojo.

Podemos emplear la libertad de escoger b para fijar el valor de un peso. Si tomamos b = (w_n/w₀)^1/n, conseguimos que los pesos primero y último sean iguales, w'₀ = w_n = w' _n.

Sin pérdida de generalidad, podemos fijar los pesos inicial y final de la curva y tomarlos iguales a la unidad, w₀ = 1 = w_n.

3  Cónicas

Vídeo de Cónicas

Las parametrizaciones racionales describen arcos de todo tipo de cónicas. Fijémonos en la parametrización normalizada, w₀ = 1 = w₂, w₁ = w, de una curva racional de grado dos,

Considerando sólo pesos positivos, para 0 < w < 1 tenemos un arco de elipse. Para w = 1, tenemos un arco de parábola. Para w > 1, se trata de un arco de hipérbola. Ejemplo

Vídeo de Ejemplo de cónicas

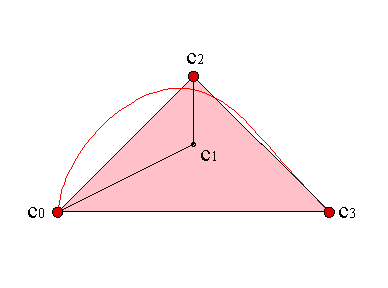
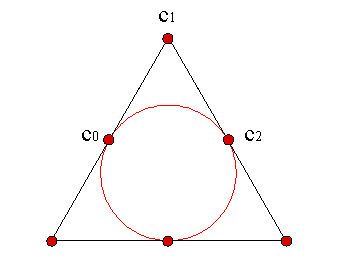
Una sencilla construcción geométrica nos proporciona los vértices del polígono de control de un arco de circunferencia.

A la vista de la figura, si situamos el centro en (0,0) y los extremos c₀, c₂ en (-Rsinα,Rcos α), (Rsinα,Rcosα), respectivamente, el vértice c₁ estará en (0,R/cosα).

El valor del peso es w = cosα. Por ejemplo, para trazar un cuadrante de circunferencia, el peso toma el valor 2^1/2/2 y para un arco de 2π/3, el peso toma el valor 1/2.

El caso límite, media circunferencia, se puede trazar recurriendo a vectores de control, Ejemplo

4  Elevación del grado

Si multiplicamos numerador y denominador por una misma función f(t), la parametrización permanece invariable por cancelación, aunque las expresiones de ambos se alteran notablemente. Dado que nuestro propósito es elevar el grado en una unidad, escogeremos la función más general de grado uno,

Si tomamos α = 1 = β, recuperamos la fórmula de elevación del grado vista en el tema anterior.

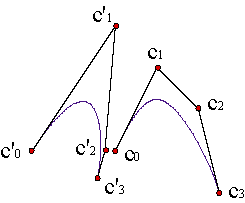
El proceso de elevación del grado (5) no conmuta con las reparametrizaciones (4). Es decir, si elevamos el grado de una curva racional y luego la reparametrizamos, no obtenemos la misma parametrización que si reparametrizamos primero y luego elevamos el grado, tal como vemos en la figura.

5  Algoritmo de de Casteljau

Vídeo de Algoritmo de De Casteljau y derivación

El algoritmo de de Casteljau se generaliza a curvas racionales,

6  Derivadas

Vídeo de Algoritmo de De Casteljau y derivación

Si escribimos, para un polígono de control {c₀,... ,c_n}, y una lista de pesos, {w₀,... ,w_n},

Estas expresiones son harto complicadas, ya que involucran derivadas de orden inferior tanto del numerador como del denominador.

Por las fórmulas para las derivadas de parametrizaciones polinómicas,

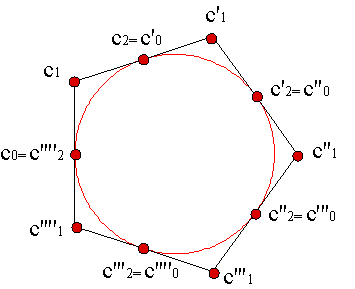
Si tenemos dos curvas racionales definidas por sus polígonos de control, {c₀,... ,c_n}, {c'₀,... ,c'_n}, y sus listas de pesos, {w₀,... ,w_n}, {w'₀,...,w'_n}, definidas en los respectivos intervalos [u₀,u₁], [u₁,u₂], la condición para que formen una única curva continua es

Dado que c_n, c'₀ son el mismo punto, parece lógico que impongamos w_n = w'₀.

Si además pretendemos que la parametrización sea de clase C¹, deberemos exigir

A partir de la segunda derivada, las cosas se complican. Sin embargo, podemos aprovecharnos de la enorme libertad que ofrecen las parametrizaciones racionales para imponer una condición suficiente, aunque no necesaria, para que la parametrización de una curva compuesta sea de clase C^r.

7  Interpolación y aproximación

Las curvas racionales aportan muchos grados de libertad adicionales a las curvas de Bézier, que podremos emplear para mejorar las soluciones de los problemas de interpolación y aproximación.

Podemos ver el problema racional como un problema polinómico en R³ en el que los datos son los valores c(t_i) = a_i, i = 0,...,m, donde a_i = (v_i,v_ia_i). Como los datos del problema son de la forma c(t_i) = a_i, quedan como parámetros libres los pesos de los puntos dato, v_i, i = 0,...,m.

No existen algoritmos generales para determinar dichos pesos, así que deberemos considerarlos grados de libertad en el diseño, que nos permitirán mejorar las propiedades de la curva resultante. Ejemplo