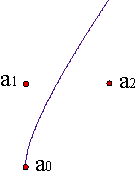
Para el diseño es conveniente emplear representaciones sencillas de curvas y superficies. Podríamos representar curvas polinómicas de grado n:
| ||||
Esta representación no es muy práctica, ya que no nos da una idea clara del comportamiento de la curva.
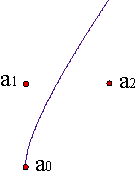
Por otra parte, si queremos observar la curva desde otro punto de vista, rotándola, trasladándola,... el comportamiento de los coeficientes es de lo más variopinto. Ejemplo.
Además, esta representación no es muy estable frente a pequeños cambios. Imaginemos que tenemos una parametrización con sólo coeficientes a0, a1 no nulos, es decir, la correspondiente a un segmento de una recta. Cualquier pequeña fluctuación daría lugar a coeficientes ai pequeños, pero no nulos. Y una curva de grado n es cualitativamente muy distinta de una recta. Ejemplo.
Por todo ello, parece conveniente emplear una representación distinta de las curvas polinómicas.
Una base distinta para los polinomios de grado n nos la proporcionan los polinomios de Bernstein,
| |||||||||||||
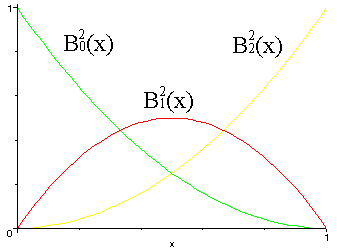
Podremos representar las curvas polinómicas de grado n como combinación de estos polinomios
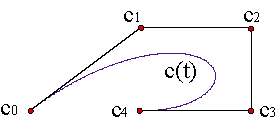
| |||||||
Aunque hayamos definido la curva en el intervalo [0,1], es posible utilizar otros intervalos. Sólo hace falta transformar el intervalo para que la parametrización esté definida en el intervalo [a,b],
| ||||||
| ||||||
Nótese que la parametrización c(t) no ve el intervalo [a,b], sino el [0,1]. Es sólo un ajuste del usuario. Ejemplo.
Dos de los vértices del polígono de control tienen una interpretación inmediata. La curva pasa por los vértices c0, cn,
| ||||
El nombre de polígono de control hace referencia a que sirve para controlar la forma de la curva. Sin embargo, ese control no es local, ya que, desplazando un vértice, se mueve toda la curva, aunque principalmente la parte más próxima al vértice en cuestión. Ejemplo.
La curva está contenida en la envolvente convexa del polígono de control. Así pues, como su nombre indica, el polígono nos proporciona una primera idea de por donde pasa la curva. Ejemplo.
Además, la transformación de la curva por una aplicación afín f, es sencilla, ya que
| ||||||
Finalmente, las curvas de Bézier son simétricas. Si invertimos el polígono de control, {cn,...,c0}, la gráfica de la curva es la misma que la correspondiente a {c0,...,cn}, sólo que es recorrida en sentido inverso. Ejemplo.
La manera tradicional de trazar las curvas de Bézier está basada en el algoritmo de de Casteljau.
El algoritmo de de Casteljau consiste simplemente en la aplicación reiterada de la interpolación al polígono de control de la curva de Bézier,
| |||||
| |||||
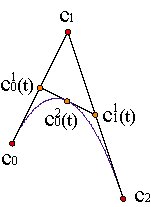
| |||||
Las ventajas del algoritmo de de Casteljau son su sencillez y el hecho de que involucra tan sólo sumas, ya que todos los términos son positivos. Ejemplo de parábola. Ejemplo de cúbica.
Una construcción muy útil basada en el algoritmo de de Casteljau es el blossom, que denominaremos polar de la parametrización, debido a que está relacionado con esta del mismo modo que una forma cuadrática con su forma bilineal asociada, también llamada polar.
La idea es la siguiente. En vez de interpolar siempre para el mismo valor de t en los n pasos del algoritmo, interpolamos en el valor t1 en el primer paso, en el valor t2 en el segundo, ... y en el valor tn en el último. Obtenemos así un punto que denotaremos c[t1,...,tn]. No se corresponde con ningún punto de la curva, salvo en el caso trivial en el que todos los ti son iguales.
Veámoslo con un ejemplo sencillo, el caso n = 2, para el polígono de control {c0,c1,c2}:
| |||||||||||||
La polar es simétrica, es decir, c[t1,t2] = c[t2,t1]. Este resultado se generaliza a curvas de grado n. Ejemplo
La polar permite reconstruir el polígono de la curva de Bézier.
| |||||||
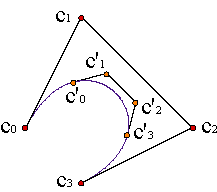
Es útil para restringir el intervalo de definición de una curva de Bézier, c(t), definida en el intervalo [0,1]. Conocemos el polígono de control {c0,...,cn} de la curva primitiva, pero no el de su restricción al intervalo [a,b] Ejemplo. Los vértices del polígono de control de la curva restringida serán
| ||||||||||
En algunos casos, nos puede interesar cambiar el grado de la curva para tener más grados de libertad a la hora de modificarla. La curva de grado n de polígono {c0,..., cn} y la curva de grado n+1 y polígono {c10,...,c1n+1} dado por
| |||||||||
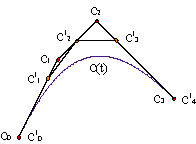
Si iteramos el proceso de elevación del grado, esencialmente estamos "redondeando" el polígono de control, recortándole las esquinas. En el límite de infinitas elevaciones de grado, el polígono tiende a la forma de la curva, aunque no es un procedimiento eficiente para trazarla. Ejemplo
La elevación del grado no es la panacea universal para conseguir curvas más versátiles, ya que sabemos que los polinomios presentan mayor variación a medida que incrementamos el grado.
Otra propiedad es la disminución de la variación. Una recta r corta a una curva de Bézier, c(t), en a lo sumo tantos puntos como a su polígono de control, {c0,...,cn}. Ejemplo
El problema inverso, la disminución del grado, como es obvio, no tiene en general solución, ya que una curva de grado n+1 real no se puede expresar como una curva de grado n, pero se puede estudiar la mejor aproximación al problema de disminución del grado por mínimos cuadrados.
La derivada de la parametrización de una curva de Bézier, es decir, el campo tangente a la curva, es
| |||||||||
La derivada de una parametrización de Bézier de grado n es otra parametrización de Bézier de grado n-1 para una curva vectorial de polígono de control dado por {nΔc0,...,nΔcn-1}.
Como la curva pasa por los vértices inicial y final, tenemos que
| |||||||||
Esta expresión se puede generalizar a derivadas superiores por simple iteración:
| ||||||||||||||
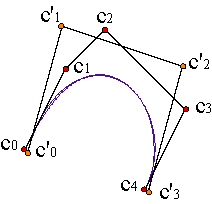
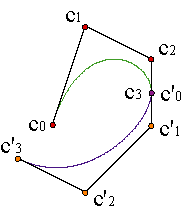
Supongamos que deseamos enlazar dos curvas de Bézier de grado n, definidas en los intervalos adyacentes [u0,u1], [u1,u2], con polígonos respectivos {c0,..., cn}, {c'0,..., c'n}. Si la curva es continua, deberemos tener c(u1) = c'(u1), es decir, cn = c'0.
Si además queremos que la curva compuesta definida en el intervalo [u0,u2] tenga una parametrización de clase C1, es decir, con tangente continua, deberemos exigir:
| ||||||||
El grado n ha desaparecido por cancelación en la expresión. La condición sobre las derivadas de la parametrización se traduce en una condición sobre las diferencias de los vértices. Ejemplo
La condición para que la curva sea de clase Cr es fácil de deducir:
| |||||||||
Las curvas de Bézier pueden utilizarse para interpolar entre varios puntos, conocidos los valores que les corresponden del parámetro t. Supongamos que tenemos n+1 puntos {a0,...,an} y queremos obtener una curva c(t) definida en el intervalo [0,1] que verifique
| ||||
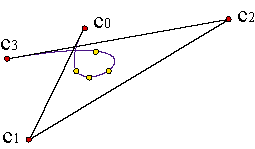
Para resolver el problema de interpolación, debemos encontrar el polígono de control de la curva de grado n que verifique
| ||||||
| ||||||||||||||||||||||||||||||||||||||||
En notación matricial, nuestro sistema es BC = A, donde B es la matriz de los valores de los polinomios de Bernstein en t0,... ,tn, y C,A son las matrices cuyas filas son las componentes, respectivamente, de los vértices del polígono de control y de los datos del problema. La solución formal sería C = B-1A, aunque la manera eficiente de obtenerla será por algún algoritmo de resolución numérica. Ejemplo.
Finalmente, incluimos una pequeña aplicación de interpolación para poder comprobar lo estudiado hasta el momento.
Es más interesante el caso en el que tenemos m+1 puntos y queremos obtener la curva de grado n que más se aproxime a nuestro conjunto de puntos por mínimos cuadrados.
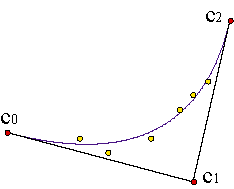
En vez de resolver el sistema BC = A, de m+1 ecuaciones y n+1 incógnitas, resolveremos el sistema BtBC = BtA, que es un sistema de n+1 ecuaciones y n+1 incógnitas. El problema tiene solución única. Ejemplo.