Tensor product patches are a great contribution to surface design, but there are other procedures for creating surfaces, some of them developed before the NURBS appeared.
These other formalisms are based on curves. It is standard for the industry to start up with sections (represented by a mesh of curves) of ships, aircrafts... and then fill in the space between them with some sort of surface and, at the same time, with some limitations on tolerances, curvature, volume, hydro or/and aerodynamic smoothness...
Our aim in this chapter is to describe in a simple way procedures for filling the space between several curves with a surface. We shall talk about ruled, translational, developable and Coons patches.
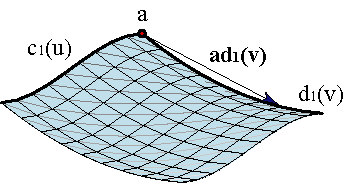
A translational surface is a simple solution to the problem of interpolating a surface passing through two curves: let c1(u) and d1(v), with u,v∊[0,1], be two such curves, intersecting at a common point c1(0) = a = d1(0). We want to find a parametrized surface c(u,v) that passes through both curves such that c(0,v) = d1(v), c(u,0) = c1(u).
The translational surface parametrization is defined by:
| (1) |

This expression means translating c1(u) parallel to itself along the curve d1(v). Example. That is: translating the point c1(u) by the vector ad1(v).
Notice that this surface has identically zero twist everywhere,
| (2) |
These are translational surfaces .
Let us apply what we know about curves for constructing these patches.
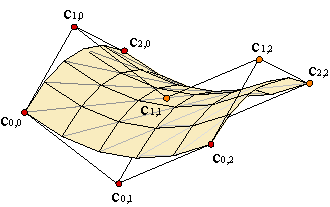
Given two Bézier curves of degree m and n, c1(u), d1(v), with respective control polygons {c10,...,c1m}, {d10,...,d1n}, let us assume that their common point is c10 = a = d10. As the translational surface c(u,v) contains them, the control polygons give us a column and a row of the boundary of the control net. The other vertices can be found thanks to the zero twist condition. Example. In our case,
| (3) |
This relation is also valid for B-spline surfaces. For rational or B-spline rational surfaces, weights have to be added,
| (4) |
Assume that we have two curves c1(u), c2(u), parametrized over the same interval u∊[0,1] and we want to construct a surface c(u,v), whose boundary contains both of them,
| (5) |
The most elementary solution consists on linking every point of c1(u0) with the one from the other curve with the same u value: c2(u0), with a straight line. These are ruled surfaces or lofted surfaces. Example. The parametrization of a ruled surface is:
| (6) |
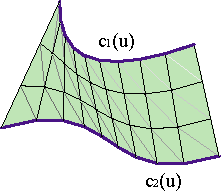
Building up ruled Bézier surfaces is not a problem: given two curves of degree m, c1(u), c2(u), and control polygons {c10,..., c1m}, {c20,...,c2m}, the ruled surface will be necessarily of degree (m,1) and consequently the control net will be formed by the polygons of both curves {c10,c20,..., c1m,c2m}.
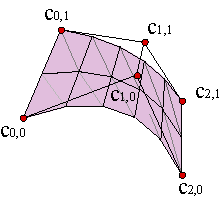
This result is valid also for ruled B-spline surfaces. For rational or B-spline rational surfaces, we only need to add the weight matrix that, accordingly with the previous reasoning, is formed with the weights of both curves, {w10,w20,..., w1m,w2m}.
A particular case of ruled surfaces are developable surfaces. Geometrically, its main characteristic is having zero Gaussian curvature. They are plane or plane regions that can be immersed into space without deformation. Because of that, they can be extended onto a plane: that is the origin of the name: developable surfaces.
Consider a developable surface parametrized by c(u,v). If n(u,v) is a normal vector to the surface at the point c(u,v), the condition of zero Gaussian curvature is:
| (7) |
This result expresses that the surface is developable if cuv(u,v), cu(u,v), cv(u,v) lie in the same plane, for every value of the parameters.
The condition (7) also states that a ruled surface is developable if and only if for every pair of homologous points, the generators of the curves and the lines that connect them lie in the same plane.
Simple examples of developable surfaces are cylindrical and conical surfaces, besides the plane itself.
Cylindrical surfaces are ruled surfaces where the curves c1(u), c2(u), can be obtained one from the other by a translation,
| (8) |
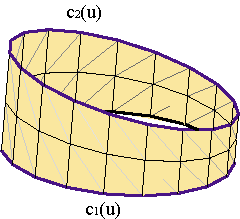
Cylindrical surfaces can be interpreted as translational surfaces where the second curve is a line, d1(v) = a + v v. Or, more generally, the cylindrical surfaces are ruled surfaces where all generatrices are parallel. The generatices are the lines with u = const in the ruled surfaces.
Straight lines on a ruled surface are called rulings. If all rulings are parallel, our surface is cylindrical; if all intersect in a point, we have a conical surface. Given a as fixed point,
| (9) |
It is not easy to characterize developable surfaces of degree (1,n) in terms of their control net.
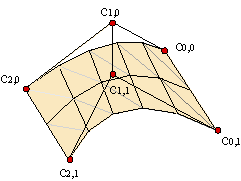
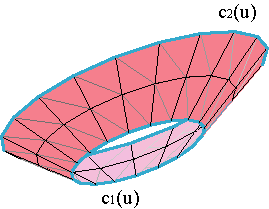
Consider four parametrized curves, c1(u), c2(u), d1(v), d2(v), u,v ∊[0,1], which form a curved quadrangle,
| ||||||||||||||
and we want to find a surface c(u,v) that contains all four curves,
| ||||||||||||||
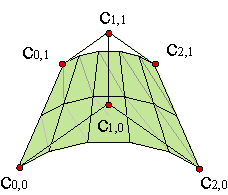
A simple solution is: denote by cc(u,v) the ruled surface that leans on c1(u) and c2(u), denote by cd(u,v) the one which leans on d1(v) and d2(v),
| |||||
Summing cc(u,v) and cd(u,v), and substracting another ruled surface, a hyperbolic paraboloid, that interpolates between the four corner vertices,
| ||||||||||||||
we find a parametrization that is the solution to our problem,
| (14) |
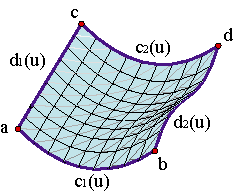
These surfaces are called Coons surfaces and generalize ruled surfaces. Example.
Let us describe now polynomial Coons surfaces.
Let c1(u), c2(u) be curves of degree m and respective control polygons {c10,..., c1m}, {c20,..., c2m}.
Let d1(v), d2(v) be curves of degree n and control polygons n {d10,..., d1n}, {d20,...,d2n}.
In order to obtain the net of the Coons surface, we have to elevate the degree of the auxiliary surfaces to (m,n). Example. The vertices of the control net of the Coons surface, {c0,0,..., cm,n}, can be expressed as
| (15) |
in terms of the vertices of the ruled surfaces,
| |||||||||||||||||||||||||||||||||||||||
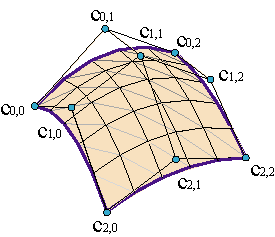
In the same way, we can construct B-spline Coons surfaces, using the insertion algorithm to provide three auxiliary surfaces with the same knots.
First we elevate the degree of the three parametrizations in order to reach degree (m,n) and then we insert the common knots in order to have the same knot sequences.
Rational Coons surfaces can be constructed either, but it is not trivial to provide control nets and weights for them.

Coons surfaces can interpolate a mesh of spatial curves, such that every curved quadrangle defines a Coons surface.
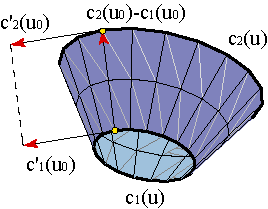
Consider one Coons surface. If we want to join it with another surface along the curve u = 1, d2(v), we find that the transversal derivative along the boundary is:
| ||||||||||||||||
We see here an unwanted effect. The value of the transversal derivative at u = 1 depends on the values at u = 0, that is to say, depends on the opposite curve d1(v). This makes difficult to match another surface with continous tangent. Example.
A solution will be using polynomial cubic splines B30(u)+B31(u) and B32(u)+B33(u) as interpolation functions or using Bernstein polynomials of degree 3.
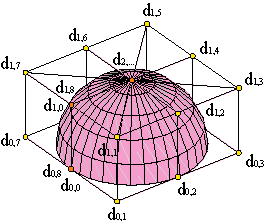
Surfaces of revolution are formed by rotating a plane curve (called generatrix) around an axis contained in the same plane as the curve. Example.
For instance, if the curve is contained into the XZ plane, c1(u) = (f(u),0,g(u)), a parametrization will be (rotating around Z axis):
| (18) |
The v = const parameter lines are the meridians of the surface. The u = const curves (circumferences of radius ¦f(u)¦) are the parallels of the surface.
Hence, constructing the control net of a surface of revolution generated by a rational planar curve with control polygon {c0,..., cn} and weights {w0,...,wn}, is simple: rotate every polygon to every position of the vertices of the circumference, multiplying by one-half (21/2/2 in case of four arcs) the weights of the intermediate vertices, the ones that do not lie on the circumference.
Consequently, meridians are described by columns of the net and parallels, by rows.
The previous construction is also valid for B-spline curves.
The procedure is essentially the same: first we have to translate the previous polygon to every point of the B-spline polygon of the curve that is going to be rotated, modifying radius, heights and multiplying by weights, as we did for Bézier surfaces of revolution.