Integración clásica
Historia
Históricamente la integración se remonta a los antiguos egipcios. En el Papiro matemático de Moscú, de alrededor del 1800 AC, se muestra la fórmula del volumen de un tronco piramidal. De hecho, el cálculo del volumen de cualquier tronco es uno de los hilos conductores del cálculo tal y como lo conocemos. Hoy relacionamos un área con una integral:
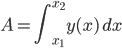 ,
,y un volumen con una integral en dos dimensiones:
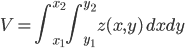 .
.Estas fórmulas, aunque exactas, plantean una serie de problemas. Por ejemplo, los límites de integración, pueden (y suelen) estar relacionados entre sí. A veces, y es lo que expongo en estas breves notas, es más sencillo remontarnos a la antigüedad y considerar las integrales como una "suma de rebanadas", sin necesidad de usar mucho cálculo.
Qué hay que saber
En estas notas, presupongo integración básica en una dimensión. En particular, las siguientes integrales sencillas: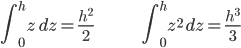
También utilizaré, y esto no es tan común, el concepto de escala, o escalado. Se refiere esto, en este contexto, al hecho de que si alteramos las dimensiones lineales de un objeto plano mediante cierta razón, el área se ve afectada for el cuadrado de esta razón. Es decir, doblar las dimensiones lineales implica cuadruplicar el área. Esto explica la subida drástica de precios de las televisiones planas, por ejemplo. De igual modo, el volumen se ve afectado por el cubo de la razón. En un libro clásico, 100 Preguntas sobre la Ciencia, Isaac Asimov usaba estas ideas para desmitificar ciertos tópicos biológicos (del tipo "las pulgas saltan 10 veces su peso") y para explicar porqué los elefantes precisan unas patas tan enormes (lo cual les impide saltar).
Áreas
Por ejemplo, el área de un cuadrado es trivial: 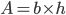 . La integral de arriba arroja esto (con
. La integral de arriba arroja esto (con 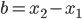 y
y 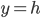 ). Pero, ¿qué hacemos para un
). Pero, ¿qué hacemos para un
paralelogramo? La integral debería, en principio, partirse en tres, porque 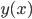 sería una "función a trozos" (cada una de las integrales es conocida, sí, pero la integral no queda muy elegante). Sin embargo, fijémonos en que, según subimos en la dirección y, la base, de longitud b, se desplaza rígidamente hacia la derecha. El "techo" mide, de hecho, también b. Así pues, necesariamente
sería una "función a trozos" (cada una de las integrales es conocida, sí, pero la integral no queda muy elegante). Sin embargo, fijémonos en que, según subimos en la dirección y, la base, de longitud b, se desplaza rígidamente hacia la derecha. El "techo" mide, de hecho, también b. Así pues, necesariamente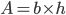 , porque según subimos en altura hasta llegar a h vamos teniendo una longitud fija b. Así "integraban" los antiguos, pensando que podían tomar finas rebanadas según iban subiendo en altura. (Nota avanzada: se puede pasar de la integral de un paralelogramo a la de un cuadrado mediante un jacobiano igual a 1, lo cual demuestra que el volumen no cambia. El ejemplo típico es el desplazamiento de una pila de naipes. Esta transformación, con el tiempo en el eje y, es justamente la de la relatividad de Galileo.)
, porque según subimos en altura hasta llegar a h vamos teniendo una longitud fija b. Así "integraban" los antiguos, pensando que podían tomar finas rebanadas según iban subiendo en altura. (Nota avanzada: se puede pasar de la integral de un paralelogramo a la de un cuadrado mediante un jacobiano igual a 1, lo cual demuestra que el volumen no cambia. El ejemplo típico es el desplazamiento de una pila de naipes. Esta transformación, con el tiempo en el eje y, es justamente la de la relatividad de Galileo.)

La fórmula de un triángulo es muy sencilla: un paralelogramo se puede dividir en dos triángulos de igual área, trazando su diagonal. Así pues, 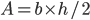 para un triángulo.
para un triángulo.
Volúmenes
Si el resultado anterior parece muy simple, consideremos volúmenes. Para comenzar, el volumen de un prisma, o de un cilindro, debe ser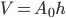 ,
,donde
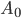 es el área de la base y h es la altura en el sentido anterior: la distancia entre los planos que contienen a las bases, incluso si el prisma, o cilindro, está "torcido". En particular,
es el área de la base y h es la altura en el sentido anterior: la distancia entre los planos que contienen a las bases, incluso si el prisma, o cilindro, está "torcido". En particular, 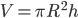 para un cilindro. Hasta ahora, es todo muy parecido a lo anterior. Pero ¿cuál es el volumen de un cono? Bastaría ver cuántos conos "caben" en un cilindro. Pero, aunque en un paralelepípedo caben dos triángulos, resulta que en un cilindro no hay sitio para dos conos, sino para tres... lo cual no es muy intuitivo.
para un cilindro. Hasta ahora, es todo muy parecido a lo anterior. Pero ¿cuál es el volumen de un cono? Bastaría ver cuántos conos "caben" en un cilindro. Pero, aunque en un paralelepípedo caben dos triángulos, resulta que en un cilindro no hay sitio para dos conos, sino para tres... lo cual no es muy intuitivo.Para hacer las cosas algo más rigurosas, consideremos una amplia clase de objetos que podemos llamar pirámides. En éstos, la base tiene una cierta área
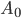 que, según subimos "hacia arriba" en
que, según subimos "hacia arriba" en  , va reduciéndose, hasta anularse en el ápice. Queremos calcular el volumen de estos objetos, pero esto será
, va reduciéndose, hasta anularse en el ápice. Queremos calcular el volumen de estos objetos, pero esto será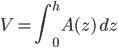 .
.La dependencia del área de cada rebanada con
 es sencilla. Cuando
es sencilla. Cuando  estamos en la base, y esta área vale
estamos en la base, y esta área vale 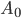 . Cuando estamos en
. Cuando estamos en 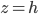 esta área se anula. ¿Qué pasa en medio? Uno estaría tentado de escribir una relación lineal
esta área se anula. ¿Qué pasa en medio? Uno estaría tentado de escribir una relación lineal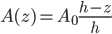 .
.Esta es la relación lineal correcta, que proporciona un factor 1 en z=0 y un factor 0 en z=h.
Esto conduciría a
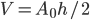 . Pero... ¡es incorrecto!
. Pero... ¡es incorrecto!Según se sube, las dimensiones de las rebanadas van disminuyendo. Como son las dos dimensiones lineales, x e y, el área decrece cuadráticamente con
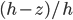 . Es decir, a media altura el área se ha reducido a una cuarta parte. Por ejemplo, para una base cuadrada de lado a, el lado a la altura z será
. Es decir, a media altura el área se ha reducido a una cuarta parte. Por ejemplo, para una base cuadrada de lado a, el lado a la altura z será 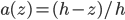 , pero el área será
, pero el área será  .
.En general:
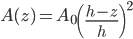 .
.Volviendo a nuestra integral (sí, acabamos integrando, pero no mucho):
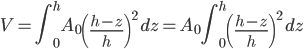 .
.La última integral se hace facilmente:
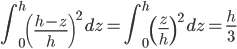 .
.Así pues,
 .
.Por ejemplo:

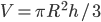 (no hemos dicho en ningún momento que forma tenía la base). (Es decir: en un cilindro hay sitio para tres conos con la misma base.)
(no hemos dicho en ningún momento que forma tenía la base). (Es decir: en un cilindro hay sitio para tres conos con la misma base.)
![V=\int_0^h A_0\left(\frac{H-z}{H}\right)^2 \, dz=\frac{A_0 H}{3} \left[ 1- (1-h/H)^3 \right]](images/EXTERN_0026.png) ,
,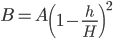 . Donde ponga H ponemos, por tanto,
. Donde ponga H ponemos, por tanto, 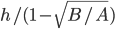 . Nos queda:
. Nos queda: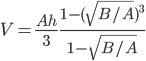 .
.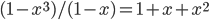 . En nuestra fórmula
. En nuestra fórmula 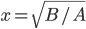 , así que
, así que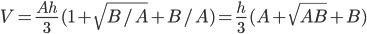 .
.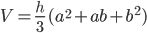 .
.