Siguiente: Primeras derivadas Subir: Derivadas de las funciones Anterior: Derivadas de las funciones Índice General
Nos centraremos en el valor de la función de forma ![]() debida
al punto (``nodo'' o ``partícula'')
debida
al punto (``nodo'' o ``partícula'') ![]() ,
situado en
,
situado en ![]() en el espacio
en el espacio ![]() , en otro punto
, en otro punto ![]() .
El vector relativo de posición es
.
El vector relativo de posición es ![]() ;
por simplicidad, omitiremos en muchas ocasiones el subíndice,
salvo cuando sea necesario expecificarlo, y escribiremos
tan solo ''
;
por simplicidad, omitiremos en muchas ocasiones el subíndice,
salvo cuando sea necesario expecificarlo, y escribiremos
tan solo ''![]() ''.
''.
Definimos
| (A.1) |
En 1D esto significa simplemente
| (A.2) |
| (A.3) |
La función de forma ![]() tiene el valor
tiene el valor
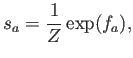 |
(A.4) |
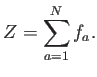 |
(A.5) |
Nuestra tarea es resolver el problema
Observamos que la derivada de ![]() con respecto
a cualquier variable
con respecto
a cualquier variable ![]() puede escribirse, gracias
a la regla de la cadena:
puede escribirse, gracias
a la regla de la cadena:
Si probamos
![]() obtenemos
obtenemos
Similarmente, si
![]() obtenemos
obtenemos
Para completar todas las posibilidades, si ![]() obtenemos
obtenemos
La minimización se lleva a cabo numéricamente mediante, por ejemplo,
gradientes conjugados (ya que las fórmulas anteriores proporcionan el
gradiente de la función que hay que minimizar); no es necesario ningún
cálculo adicional para el valor de las funciones de forma ![]() .
Hemos empleado para estos métodos numéricos estándar las bibliotecas
GSL (Gnu Scientific Libraries) en lenguaje C [34].
.
Hemos empleado para estos métodos numéricos estándar las bibliotecas
GSL (Gnu Scientific Libraries) en lenguaje C [34].
Daniel Duque 2011-11-10